Come detto, il problema fisico è veramente ridicolo: basta uguagliare le forze di gravità agenti sull’astronave causate dalle due masse M₁ e M₂.

La differenza della rappresentazione grafica sta tutta nella scelta del modo di descrivere la distanza del punto di equilibrio E dalle due masse.

Iniziamo chiamando d₁ la distanza M₁E e d₂ la distanza M₂E.

Abbiamo la semplice formula:

GM₁m/d₁² = GM₂m/d₂²        …. (1)

che diventa:

M₁/d₁² = M₂/d₂²

Bene, potremmo già decidere cosa considerare come variabile x e cosa considerare come variabile y. Vi sono, però, molte possibilità che ci permettono di giocare attorno a un’unica soluzione fisica. La matematica si diverte…

Ovviamente dobbiamo conoscere le masse delle due stelle, ma è inutile trascinarsi dietro i due valori: è molto meglio considerarne solo il rapporto. In tal modo è facile generalizzare il risultato grafico. Lo stesso rapporto va bene sia per una pianeta e un suo satellite, sia per due stelle, sia per una stella e un pianeta, ecc., ecc.

Poniamo, quindi:

M₁/M₂ = x

La (1) può scriversi:

(d₁/d₂)² = x

La cosa più ovvia sembrerebbe considerare come variabile y il rapporto tra d₁ e d₂. Avremmo subito:

y² = x         …. (2)

Ossia:

y = x^1/2       …. (3)

La funzione da rappresentare non è altro che la funzione radice quadrata. E’ difficile da disegnare? Assolutamente no. Ci si può arrivare senza fare molti calcoli.

Guardiamo la (2)… se y fosse x e x fosse y, avremmo, immediatamente, l’equazione di una parabola con vertice nell’origine (y = x²), che conosciamo molto bene (Fig. 1a). Non ci resta quindi che ruotare di 90° il grafico della parabola, sostituendo x con y (Fig. 1b). Descriveremmo una parabola con l’asse orizzontale.

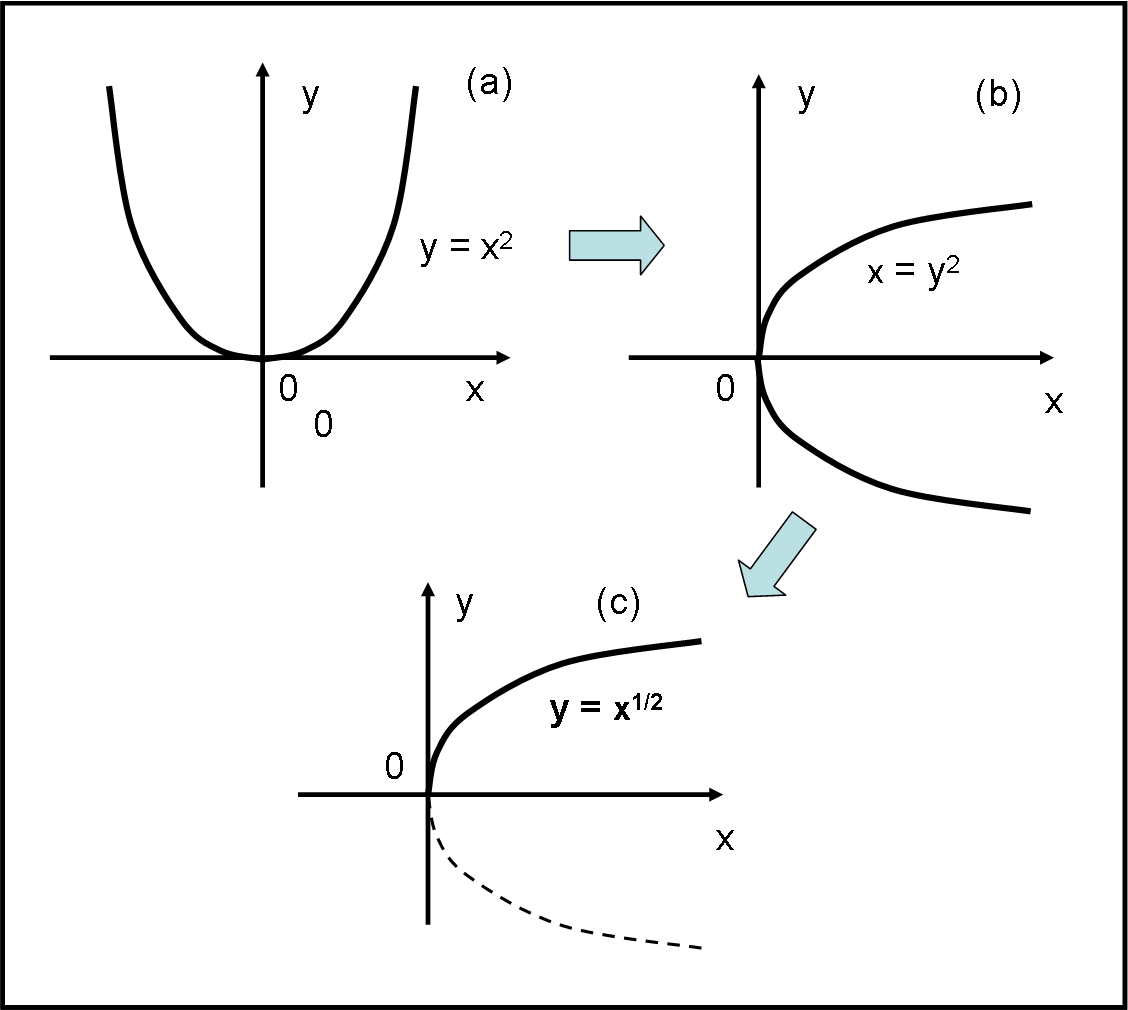
Tuttavia, noi siamo interessati alla (3) ed essa non può esistere in tutto lo spazio. Perché? Perché la y non può essere negativa, dato che questo comporterebbe una radice quadrata negativa che, per noi, è un assurdo. Dobbiamo limitarci quindi a un solo ramo della parabola “orizzontale”  quello con y positiva.

Abbiamo, infine, la Fig. 1c che descrive proprio la funzione radice quadrata. Una funzione che possiamo anche studiare da sola, ma che può essere descritta perfettamente conoscendo ciò che fa la parabola… Sappiamo che la parabola y = x² ha un minimo nell’origine e quindi una tangente orizzontale. Sappiamo anche che per x che tende a infinito, anche la y tende a infinito.

Ciò comporta che la x = y² (ossia la x^1/2 = y) ha una tangente nel vertice che è verticale. Ciò vuole anche dire che la derivata prima calcolata nell’origine deve valere infinito. Proviamo?

y = x^1/2

y’ = 1/(2 x^1/2)

y’(0) = + ∞

La derivata non si annulla mai (se non all’infinito) ed è sempre positiva, ossia la funzione è crescente.

Inoltre, per qualsiasi valore di x diverso da zero, la derivata seconda è sempre negativa, ossia la curvatura è diretta verso il basso.

Beh… potevamo capirlo senza troppi calcoli.

Cosa dobbiamo fare, adesso, per risolvere graficamente il nostro problema fisico?  Per diversi valori del rapporto di massa vogliamo trovare la distanza del punto di equilibrio. Cosa ci dice la funzione descritta prima? Analizziamola attentamente…

(a) M₁/M₂ = 0  porta a M₁ = 0 (trascuriamo il caso di masse infinite, ovviamente). Dalla curva otteniamo immediatamente che d₁/d₂ = 0 e quindi d₁ = 0. Il punto di equilibrio coincide con l’origine dato che è presente la sola massa M₂. Ma ha senso parlare di punto di equilibrio? E’ molto meglio concludere che d₁/d₂ = 0, perché d₂ = + ∞. Infatti, questo risultato è decisamente più fisico: se vi è una sola massa in gioco (M₂) l’astronave risente sempre della sua gravità fino all’infinito! Nessuno può controbilanciarla.

(b) Per M₁/M₂ = 1 (M₁ = M₂)  si ha che d₁= d₂, ossia il punto di equilibrio sta nel punto di mezzo tra le due masse. Questo è vero per qualsiasi distanza tra le due stelle.

(c) Per M₁/M₂ = + ∞ (M₂ = 0) si ha che d₁/d₂ = + ∞. Anche qui potremmo matematicamente concludere che d₂ = 0, ma, nuovamente concluderemmo che il punto di equilibrio si trova dove non esiste nessuna stella! Molto più fisica è la conclusione d₁ = + ∞, ossia che in qualsiasi punto dello spazio si fa sentire solo e soltanto la gravità di M₁.

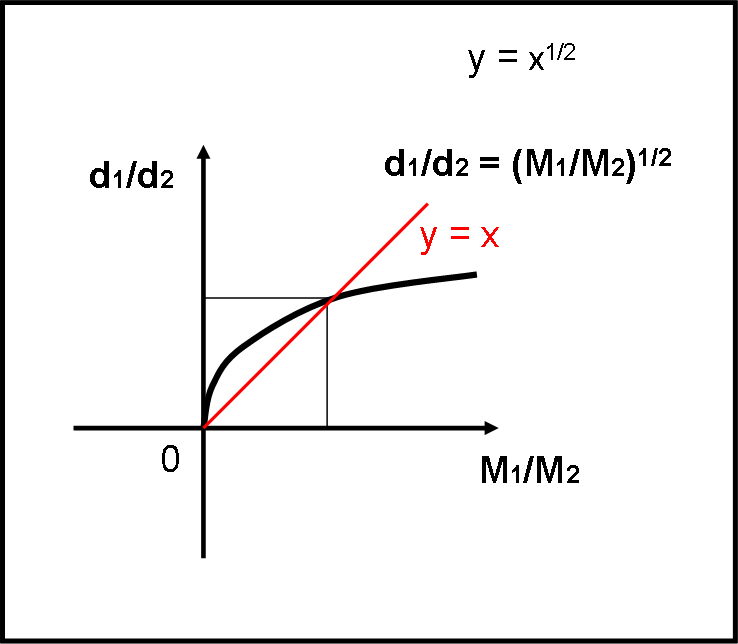
Una soluzione molto elegante, direi… ma siamo proprio sicuri che sia così utile? Vi faccio notare una situazione molto particolare che è tipica della parabola y = x² e quindi anche della funzione y = x^1/2. Essa coincide in tre punti con una funzione molto più banale, la retta y = x.

Infatti, per x= 0 si ha y = 0; per x= 1, si ha y = 1 e per x = + ∞ si ha y = + ∞. In Fig. 2 ho tracciato la retta y = x e quanto detto risulta immediato.

In altre parole, finora abbiamo evitato un po’ di ostacoli girandoci intorno.

Potevamo già capirlo per il caso M₁ = M₂. Sapere che il punto di equilibrio era il punto a metà strada diceva poco. Sarebbe stato necessario viaggiare a velocità costante da M₁ a M₂, calcolare il tempo impiegato, e poi tornare indietro alla stessa velocità, fermandosi quando è trascorsa la metà del tempo precedente. Insomma, un’operazione lunga e dispendiosa. Le cose peggiorano ancora se consideriamo un rapporto di masse qualsiasi, ad esempio M₁/M₂ = C. In questo caso retta e radice quadrata si allontanano tra loro. Vediamo cosa troviamo…

M₁/M₂ = C  porta a d₁/d₂ = C^1/2. Beh… che cosa ce ne facciamo? Parliamoci chiaro è un numero che ha poco senso se non conosciamo quale sia la distanza effettiva D tra le due masse.

Ammettiamo allora di conoscere anche la distanza D. Ora le cose vanno molto meglio!

Si può scrivere che

d₂ = d₁/C^1/2

Ma sappiamo per certo che:

d₁ + d₂ = D

e quindi:

d₁ + d₁/C^1/2 = D

d₁C^1/2 + d₁ = DC^1/2

e, infine:

d₁ = D C^1/2/(1 + C^1/2)     …. (4)

Oppure, ricavando d₂ …

d₁ = d₂ C1/2

d₂ C^1/2 + d₂ = D

e, infine:

d₂ = D/(1 + C^1/2)       …. (5)

Verifichiamo di non avere commesso errori…

d₁ + d₂ = D C^1/2/(1 + C^1/2) + D/(1 + C^1/2) = D (C^1/2 +1)/ (1 + C^1/2) = D

Tutto bene, meno male!

Prima conclusione: possiamo utilizzare il semplice grafico di Fig. 2, entrando con la radice quadrata del rapporto delle masse, ricavare il rapporto tra le distanze e, infine, conoscendo la distanza tra le masse, ricavare  d1 o d2 attraverso (4) o (5). Operazione compiuta, anche se dobbiamo fare qualche calcoletto aggiuntivo.

Tuttavia la (4) e la (5) ci indicano chiaramente che potremmo disegnare delle curve più immediate per entrare con le masse e uscire subito con la distanza da una delle due stelle (sempre che si conosca D). Infatti basta prendere come y direttamente d₁ e come x il solito rapporto tra le masse.

La (4 ) ci porta a:

y₁ = Dx^1/2/(1+x^1/2)

e la (5) a:

y₂ = D/(1+x^1/2)

Possiamo anche  porre tranquillamente D = 1, per generalizzare il risultato finale e ricavare d₁ o d₂ come percentuale della distanza totale (se conosciamo questa è immediato ricavare d₁ o d₂ in km o in quello che vogliamo).

Studiamo prima

y = x^1/2/(1 + x^1/2)          …. 4a

Per x = 0, ossia M₁ = 0  si ha y = 0. L’astronave si porta in M₁ dove non c’è niente, ma non è veramente in equilibrio dato che risente della gravità di M₂. La soluzione matematica va benissimo, ma quella fisica un po’ meno… Basta capire cosa significa il risultato e sentirsi obbligati a stare sempre tra M₁ e M₂.

x = + ∞ comporta invece M2 = 0 e y = + ∞/+ ∞ = ?

Nessuna paura! E’ una forma indeterminata estremamente semplice da risolvere. L’esponente della x è lo stesso sia al numeratore che al denominatore (andate a rileggervi questa "lezione"), il che comporta  che il limite della y per x che tende a infinito vale UNO. Ciò vuol dire che, se la massa M₂ si annulla, la distanza y tende al valore di D (posto proprio uguale a 1).

Per x = 1 si trova nuovamente y = 1/2

Cosa succede esattamente nel punto di origine? Ossia qual è la tangente alla curva? Basta fare la derivata di y e sostituire alla x il valore zero. Le cose si complicano un po’, ma si ottiene:

y’ = 1/(2(x^1/2 +1)²x^1/2)

y’(0) =1/(2∙0) = + ∞

Abbiamo nuovamente una tangente verticale.

Possiamo anche calcolare la derivata seconda (un bell’esercizio!) e si troverebbe:

y” = (- 3(x)^1/2 – 1)/(4(x^1/2 +1)³ x^3/2)

Che, per x diverso da zero, è sempre negativa

La curva potete rappresentarla da soli nell’ipotetica Fig. 3. Essa ci permette di entrare con il rapporto delle masse e trovare subito quanto vale la distanza M₁E.

Possiamo, però, semplificare tutta la faccenda e porre come ascissa t = x^1/2. Non è un grosso problema calcolare inizialmente la radice quadrata del rapporto delle masse e poi entrare con questo numero nel grafico per trovare la y. La funzione, però, diventa ancora più semplice:

y = t/(1 + t)

Anche questa, ovviamente, comporta y = 0 per t = 0, y = 1/2 per t = 1 e y = 1 per t = + ∞. Sembra esattamente quella di prima, ma… proviamo a calcolare la derivata prima nell’origine.

y’ = 1/(1+ t)²

Per t = 0 la tangente alla curva ha come coefficiente angolare m = 1, ossia la tangente è la retta inclinata di 45° rispetto agli assi.

La derivata seconda è immediata e vale:

y” = - 2/(1 + t)³

che è ovviamente negativa per qualsiasi valore di t (anche quello uguale a zero).

Decisamente più facile da studiare, non vi pare? La curva corrispondente è quella che potete disegnare da soli in Fig. 4.

Cosa possiamo concludere, pensandoci un attimo sopra? Che quest’ultima funzione, unita alla funzione t = x^1/2, ci riporta a quella di Fig. 3.

Proviamo, adesso, a studiare la funzione y₂, ponendo, come prima, D = 1. La y è adesso la distanza del punto di equilibrio dal punto M₂.

y = 1/(1+x^1/2)           …. 5a

Per x = 0 abbiamo y =1; per x = 1, y =1/2; per x = + ∞, y = 0. Beh… era ovvio… Le cose, in qualche modo, si invertono. Per M1 = 0, ci manda nel punto M1, ossia a distanza D = 1 da M2. Per masse uguali, nuovamente a metà strada, e per M2 = 0, nel punto M2.

Che tangente abbiamo  nel punto iniziale (0,1)?

y’ = - 1/(2(x^1/2 + 1)² x^1/2)

y’(0) = - ∞

La derivata seconda vale:

y” = (3 x^1/2 + 1)/(4 (x^1/2 + 1)³ x ^3/2)

Per x diverso da zero, essa è sempre positiva, ossia ha la concavità verso l’alto. La curva corrispondente è quella che potete disegnare in Fig. 5.

Lascio a voi ragionare sulla “somiglianza” tra questo risultato e quello relativo alla (4a) e tra la Fig. 5 e la Fig. 3.

Concludiamo utilizzando nuovamente la semplificazione iniziale cambiando la x in t = x^1/2. La funzione diventa veramente semplice:

y = 1/(1 + t)

Bene! Per t = 0, y = 1; per t = 1 , y = 1/2; per t = ∞, y = 0.

Tutto come prima, ma è meglio calcolare la tangente nel punto (0,1).

y’ = - 1/(1 + t)²

y’(0) = - 1

Il coefficiente angolare è la retta inclinata di 45°, diretta verso il basso.

La derivata seconda vale:

y” = 2/(1 + t)³

Per qualsiasi valore di t la derivata è positiva e la concavità diretta verso l’alto. La curva relativa è quella che potete disegnare in Fig. 6. Non può certo più stupire la simmetria con quanto avevate trovato in Fig. 4.

Un’ultima cosa molto importante. L’ultima funzione, e la relativa Fig. 6 (ma non solo…), rappresentano una curva ben nota a tutti noi (anche se “interrotta” nel punto (0,1)). Quale?

Fermiamoci qui, ma ci sarebbero molti altri giochi matematici da fare a partire da un banale problemino di fisica.

Penso siano ormai chiari gli scopi di questa lunga tiritera…

(1) Fare un po’ di esercizi con le derivate e con i limiti.

(2) Disegnare qualche bella curva.

(3) Mostrare come la stessa identica cosa può essere descritta in molti modi, “truccando” un po’ i parametri.

(4) Scherzare un po’ sopra la matematica, cercando di confondere le carte. Basta pensare che y₁ = t/(1 + t)  e y₂ = 1/(1 + t) portano a y₁ + y₂ = 1 e quindi a y₂ = 1 – y₁, con tutte le più ovvie conseguenze sui grafici…

Ovviamente, tutte le soluzioni che avete proposto finora vanno bene e ognuno di voi ha scelto una via che si trova sicuramente inserita nella mia "noiosa" trattazione. Scegliete pure quella che vi piace di più…

Lo so, è stato solo un gioco… al limite prendetelo come uno scherzo del primo d’aprile…