Vediamo come fare a costruire la linea di simultaneità per il caso più semplice, ossia per un sistema non in movimento.  Cosa vuol dire linea di simultaneità? Essa ci dice che tutti gli eventi che capitano su di lei devono essere simultanei, ossia devono avvenire allo stesso tempo t. Se, ad esempio, t fosse proprio zero, il luogo di questi punti dovrebbe avere sempre il valore t = 0. Nel caso che l’asse del tempo sia disegnato in verticale ricadiamo nel caso classico,in cui l’asse di simultaneità è perpendicolare a t, ossia è l’asse dello spazio x. Siamo nel classico sistema di riferimento S.

In questo sistema di riferimento, scegliendo convenientemente le unità di misura (ad esempio, anni e anni luce), la retta a 45° indica la traiettoria di un punto che si muove alla velocità della luce.

Immaginiamo, però, di non sapere che l’asse x sia asse di simultaneità e di volerlo determinare sperimentalmente. A, che sta fermo nel suo sistema di riferimento, si muove solo lungo l’asse del tempo t. Questo asse rappresenta la sua linea di Universo. A è munito di un orologio e di una lampada che accende a un certo istante. Sia A la sua posizione al momento dell’accensione della lampada.

Usiamo la Fig. 1. Il raggio di luce viaggia inclinato di 45° rispetto all’asse del tempo. Immaginiamo, ora , che gli infiniti punti che si trovano lungo questa retta accendano un loro lampadina nel momento in cui vengono raggiunti dalla luce partita da A. Questa luce “rinviata” raggiunge la retta t dopo un certo intervallo di tempo.

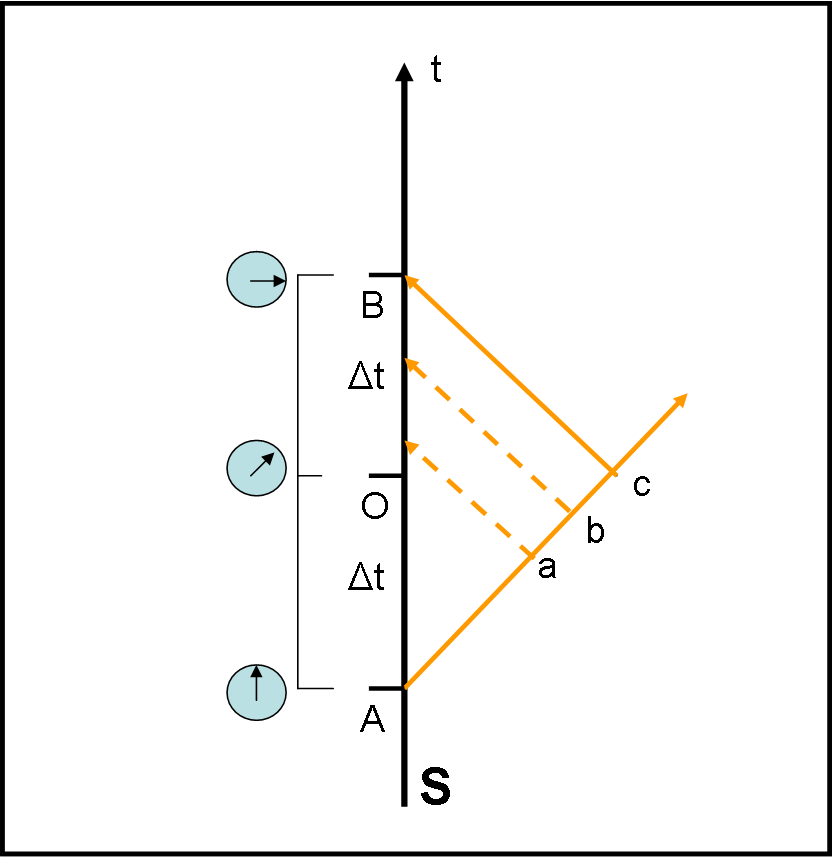
Più è lontano il punto, più tardi la luce lo toccherà e più tardi la luce rinviata dal punto toccherà la retta t. E’ indubbio, però, che l’intervallo di tempo trascorso perché la luce tocchi il punto deve essere uguale all’intervallo di tempo perché la luce riemessa tocchi la retta t. La luce viaggia a 45° ed è costante e, inoltre, i punti A e a (per esempio) non si sono mossi nello spazio, dato che sono entrambi fermi. Se la distanza spaziale è sempre la stessa e la velocità è la stessa, anche il tempo impiegato deve essere lo stesso!

Cosa deve fare allora A che ha inviato il suo segnale? Lo vediamo in Fig. 2.

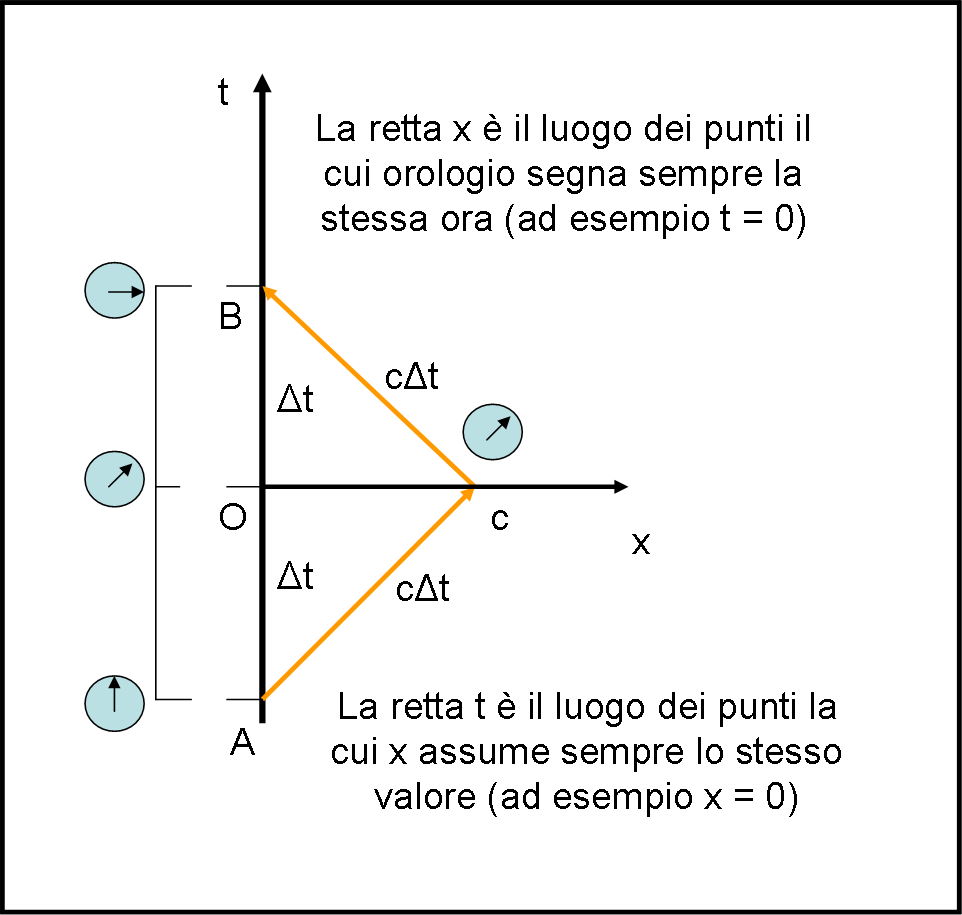
Lui viaggia tranquillamente lungo t fino ad arrivare al punto O. Non deve fare altro che guardare l’intervallo di tempo impiegato, usando il suo orologio. A non si cura assolutamente dei segnali che gli rimandano i punti dello spazio. Lui deve lasciare trascorrere un tempo uguale ad AO fino a giungere in B. Ossia deve essere sicuro che AO sia uguale a OB. O è per definizione il punto di mezzo (lo ha misurato con il suo orologio). Tuttavia, il punto c che è stato capace di ricevere il segnale mandato da A e di rinviarlo in modo che raggiunga la retta t in B, deve essere anche lui a “metà strada” esatta (il tempo di andata e ritorno DEVE essere uguale, come detto prima). Ne consegue  che quando la luce arriva in c deve essere trascorso lo stesso tempo che è servito ad A per arrivare fino a O. Esso è ancora lo stesso tempo che O impiega per arrivare in B e che la luce di c impiega per arrivare fino a B. In conclusione, il tempo dell’evento “c riceve e rinvia il segnale” e di quello “l’orologio di A arriva in O” devono essere identici.

La linea che congiunge due eventi che avvengono allo stesso tempo deve essere quella di simultaneità. Infatti, essa è proprio definita come il luogo degli eventi che avvengono alla stessa ora. Nel sistema di riferimento usato, la linea di simultaneità è proprio l’asse x, perpendicolare all’asse dei tempi.

Questa costruzione è più che infantile e non c’era certo bisogno di spiegarla così dettagliatamente. Tuttavia, ci serve per utilizzarla pari pari quando andiamo a considerare un sistema S’ che si muove rispetto a S. Dobbiamo utilizzare lo stesso e identico procedimento! Tutto diventa ovvio e banale…

Prima di cominciare, ricordiamo, però, che la velocità della luce è la stessa in ogni sistema di riferimento e tale è anche la traiettoria che descrive. Comunque si muova il sistema S’, la luce viaggia sempre a 45° rispetto agli assi del sistema S. Ricordiamo, anche, che tutto ciò che andiamo a vedere e costruire viene riferito al sistema S, che si considera fermo.

Consideriamo il sistema S’ che si muove con una certa velocità rispetto a S. Come già abbiamo imparato, descrivendo lo spaziotempo galileiano, nel sistema di S, questo movimento si può raffigurare con una retta inclinata di un certo angolo rispetto a t. L’angolo si lega direttamente alla velocità, dato che essa non è altro che uno spazio diviso un tempo.

Abbiamo perciò un nuovo asse del tempo, quello che scorre lungo la retta t’. Un oggetto fermo in questo sistema è costretto, come faceva chi era fermo in S, a descrivere l’asse del tempo t’. Anche il viaggiatore di t’ ha i suoi orologi che segnano lo stesso tempo di quelli lungo t, ma che tali non appaiono nel riferimento S che li vede rallentare. Questo problema l’abbiamo già discusso e ci torneremo sopra passando alle formule relative. Per adesso, poco c’importa come scorre il tempo su t’. L’importante è che chi viaggia lungo t’ misuri il suo tempo senza problemi.

Così come aveva fatto il viaggiatore di S, così quello di S’ accende la sua lampadina in A’, sicuro che tanti amici gli rimanderanno indietro il segnale non appena ricevuto (Fig. 3). Anche lui misura accuratamente il tempo tra A’ e O e poi aspetta che passi un tempo OB’ uguale ad A’O. In questo modo è sicuro che O sia il punto di mezzo del suo percorso. Ma, analogamente a quanto fatto da S, è interessato solo e soltanto all’amico di cui riceve il segnale di ritorno esattamente in B’.

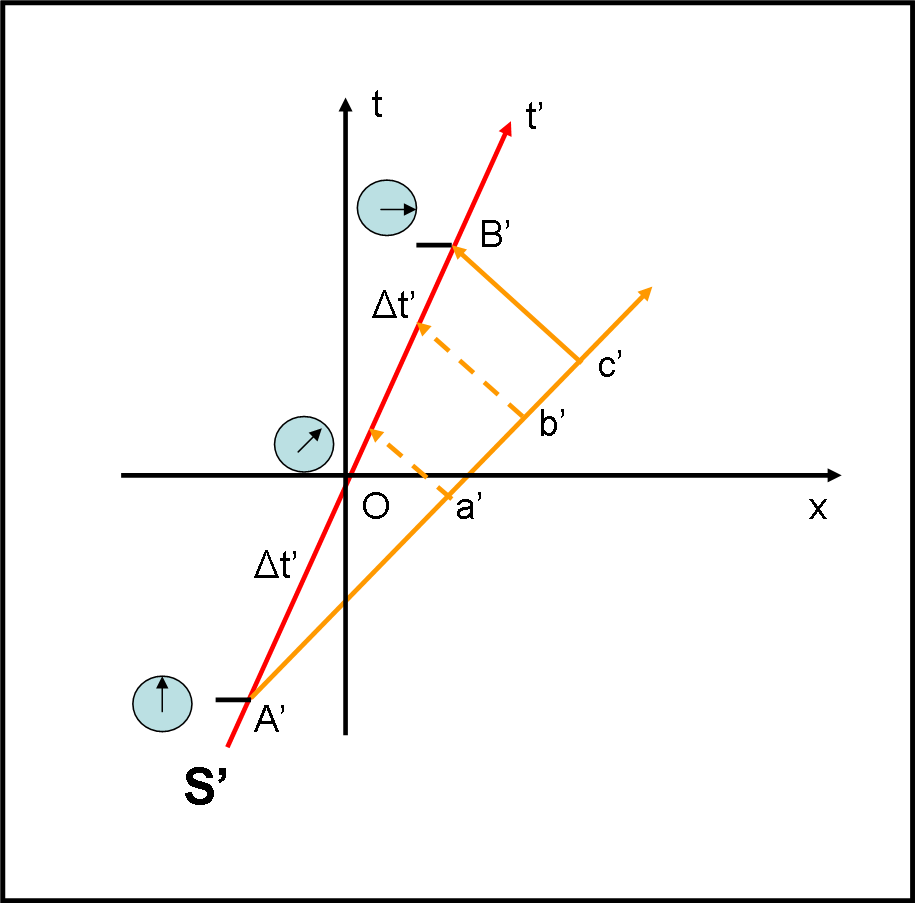
Facendo lo stesso ragionamento del viaggiatore di S, anche S’ può essere sicuro che il tempo impiegato dalla luce per andare da A’ all’amico c’ è esattamente lo stesso impiegato al segnale luminoso di ritorno per partire da c’ e arrivare in B’. Infatti, S’ è rimasto fermo spazialmente nel suo sistema di riferimento e quindi non può essere cambiata la distanza spaziale da c’. Se è uguale la distanza ed è uguale la velocità della luce, anche il tempo dell’andata deve essere uguale al tempo di ritorno. Non può che concludere che l’evento c’ che rimanda il segnale è simultaneo all’evento del passaggio di S’ da O. La retta di simultaneità deve essere, quindi, quella che congiunge O con c’. (Fig. 4).

Notate che il punto fondamentale è proprio quello di aver considerato, in qualsiasi sistema di riferimento, sempre uguale la traiettoria della luce, inclinata di 45° rispetto a t e x. Il sistema S’ ha svolto il suo compito che è perfettamente identico da quello che ha fatto S. Tuttavia, dato che questo “lavoro” lo vediamo nel sistema di S, le linee di S’ subiscono una trasformazione (che è poi quella di Lorentz!). Tanto t’ si avvicina alla traiettoria della luce, tanto fa anche l’asse x’.

E’ facilissimo dimostrarlo graficamente usando la Fig. 5.

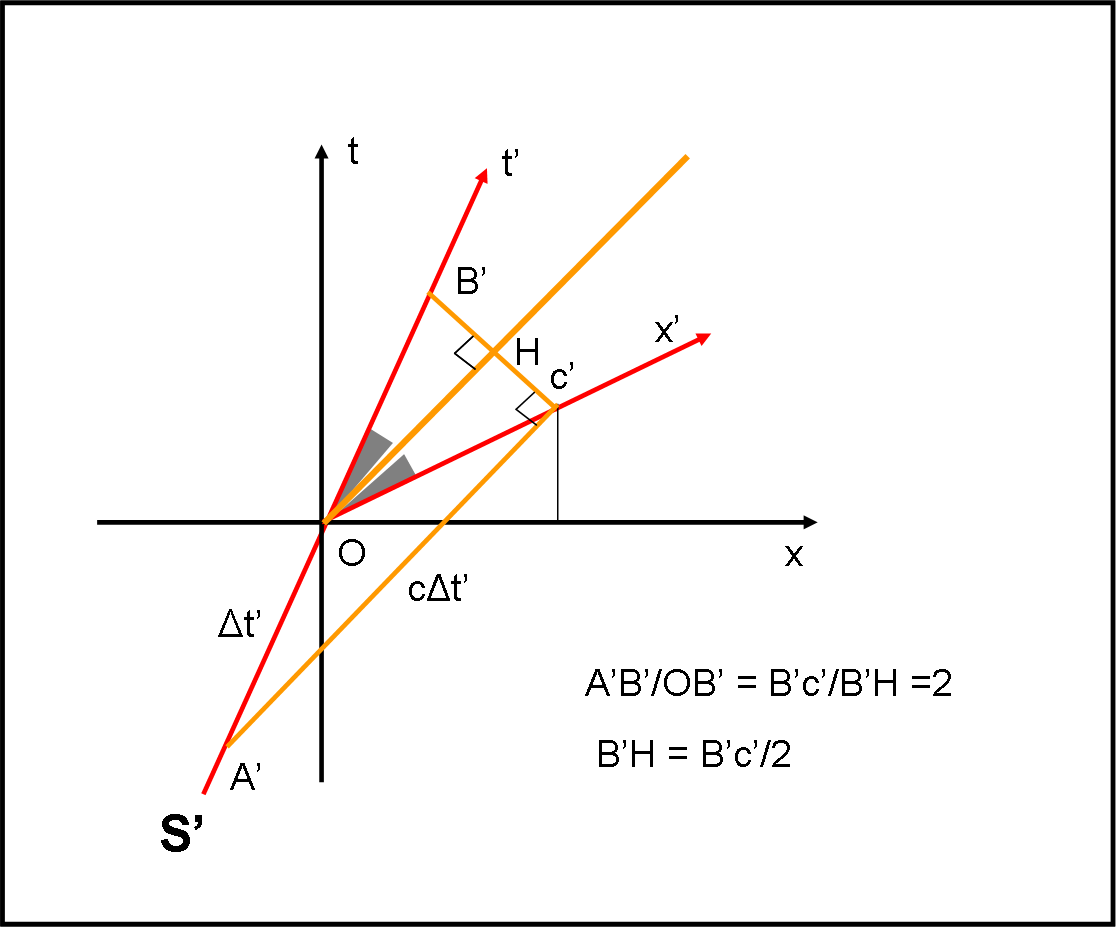
I triangoli A’c’B’ e OHB’ sono rettangoli simili, per cui deve valere:

A’B’/OB’ = B’c’/B’H

Ma

A’B’/OB’ = 2   per costruzione.

Deve quindi anche essere:

B’c’/B’H = 2

Ossia H è il punto di mezzo tra B’ e c’. Ne segue che gli angoli formati da OH con t’ e con x’ devono essere uguali.

La trasformazione di Lorentz trasforma un sistema ortogonale in un sistema non ortogonale. Lo stabiliremo, ovviamente, anche per via matematica e rigorosa.

La simmetria della trasformazione è immediatamente confermata, come mostra la Fig. 6.

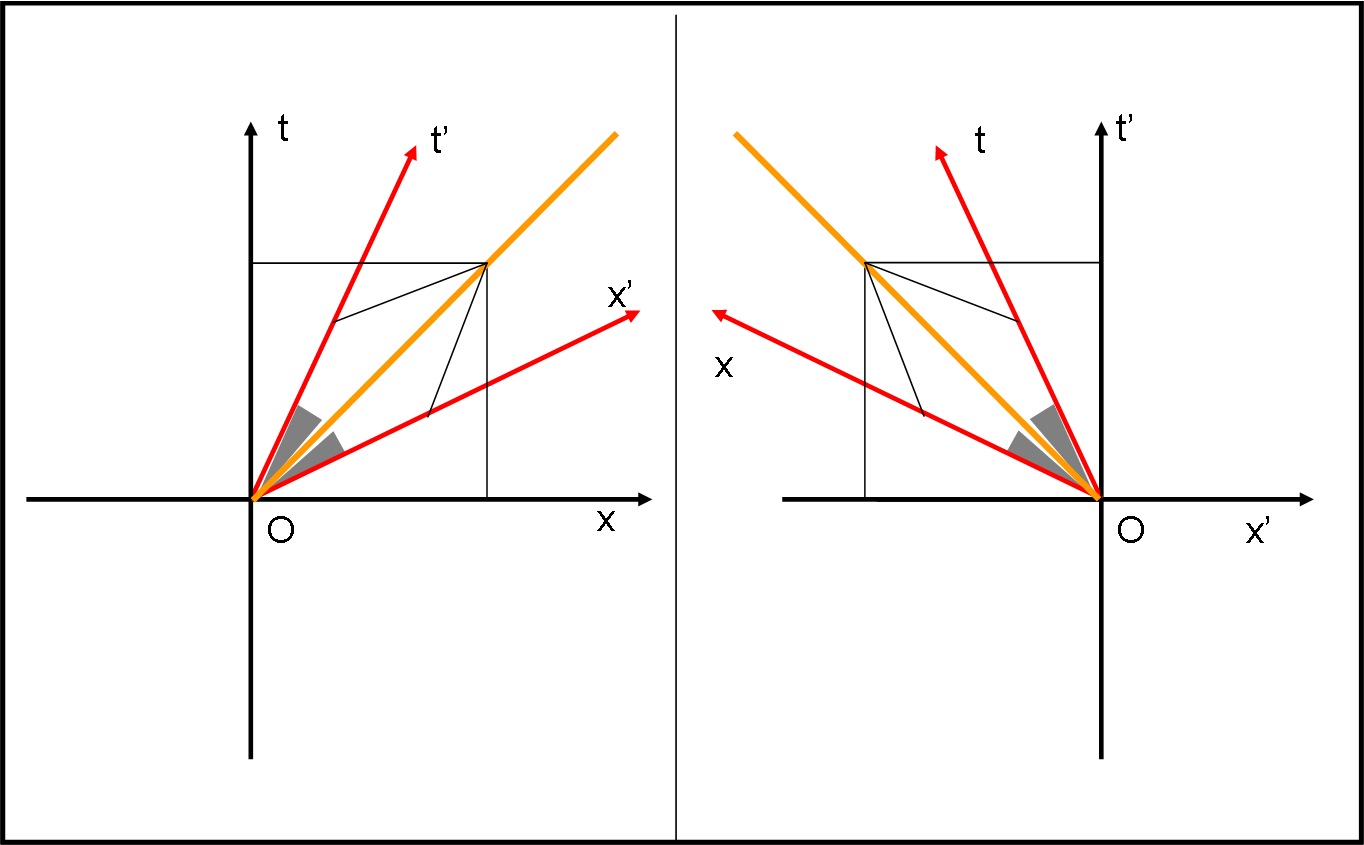
Basta fare assumere a S’ il ruolo di S. E’ lui adesso a muoversi verticalmente e la sua linea di simultaneità x’ diventa ortogonale a t’. Rispetto a lui, il sistema S si muove lungo una traiettoria diretta verso sinistra, inclinata dello stesso angolo che t’ sottendeva rispetto a t. la velocità è solo cambiata di segno. S compie un lavoro identico a quello compiuto da S’ e trova la sua linea di simultaneità. Il sistema S si trasforma in un sistema non ortogonale perfettamente simmetrico a quello che prima era S’.

Adesso, fermiamoci un po’ a riflettere e poi penseremo all’unità di misura lungo questi assi non ortogonali. Ovviamente, è sempre Lorentz che ce lo dice…