Questo articolo risponde al quiz che chiedeva di determinare analiticamente i nuovi assi x’ e t’ che derivano dalla trasformazione di Lorentz. La vera grande differenza rispetto alla trasformazione galileiana è che, ora, anche l’asse t’ dipende da x e viceversa, e quindi la trasformazione comporta una coppia di assi diversi da quelli originari. Vedremo, in particolare, che la trasformazione di Lorentz trasforma un sistema ortogonale in un sistema non ortogonale, come già anticipato nel primo quiz grafico.

Oltre a risolvere il quiz, questo articolo rappresenta, però, l’inizio del diagramma di Minkowski e deve quindi essere compreso molto bene, al di là della sua apparente banalità, dato che tutto ciò che seguirà è una conseguenza del nuovo sistema di coordinate.

Essendo una trasformazione di coordinate, essa deve dare luogo a un nuovo sistema di coordinate x’ e t’. Scusate la ripetizione, ma il concetto è fondamentale. Teoricamente potremmo non sapere “cosa” siano i nuovi assi, anche delle linee qualsiasi. Tuttavia, possiamo già anticipare che devono essere delle rette, dato che avevamo dimostrato che la trasformazione di Lorentz deve essere lineare, ossia di primo grado.

Riscriviamo ancora la trasformazione di Lorentz (escludendo y e z) e, per poter lavorare sempre con lunghezze, introduciamo la coordinata T = ct al posto di t, come già ampiamente descritto precedentemente. Il significato di tempo perde molto del suo carattere “diverso”, dato che diventa del tutto uguale alla coordinata spaziale x e come lei può essere trattata e misurata.

Le due equazioni sono:

x’ = γ(x – βT) = (x – βT) /(1 – β²)^1/2

T’ = γ(T – βx) = (T – βx) /(1 – β²)^1/2

Esse ci dicono che se un evento ha coordinate x e T, in un certo sistema di riferimento, esso ha coordinate x’ e T’ in un altro sistema, in movimento rispetto al primo con velocità v. Ricordiamo anche che β è uguale al rapporto tra velocità del sistema e velocità costante della luce c. Ripetiamo, anche, che in tale sistema di unità, la velocità di un corpo è il rapporto fra uno spostamento (in metri) e il tempo (anch’esso espresso in metri), ossia non è altro che il parametro adimensionale β.

L'abbiamo dimostrato facilmente con la semplice relazione:

v = ds/dT =ds/(cdt ) = (1/c) ds/dt = v/c = β.

Per come è stato costruito, risulta chiaro che la velocità della luce in questo sistema di coordinate assume un valore uguale a 1. Per non cadere in confusione nello scrivere le formule, ci conviene, comunque, scrivere sempre c, anche se sappiamo che il suo valore è unitario.

Torniamo alla nostra trasformazione che deve regalarci immediatamente le equazioni dei nuovi due assi x’ e T’ nel sistema di riferimento x e T. E’ questo ciò che vogliamo! Ossia, vogliamo disegnare il sistema di assi x’ e T’ nel diagramma di partenza, che ha coordinate x e T. Ne segue che dobbiamo trovare una T = g(x) e una  x = f(T) che descrivano i due nuovi assi x’ e T’.

Per ottenere il risultato voluto dobbiamo ricordare molto bene il significato di una asse di un sistema di riferimento. Il primo asse è il luogo dei punti per i quali la seconda coordinata è uguale a zero. Il secondo asse è il luogo dei punti per i quali la prima coordinata è uguale a zero.

Facciamo un esempio esplicativo, utilizzando il ben noto sistema cartesiano ortogonale definito da x e y riportato in Fig. 1.

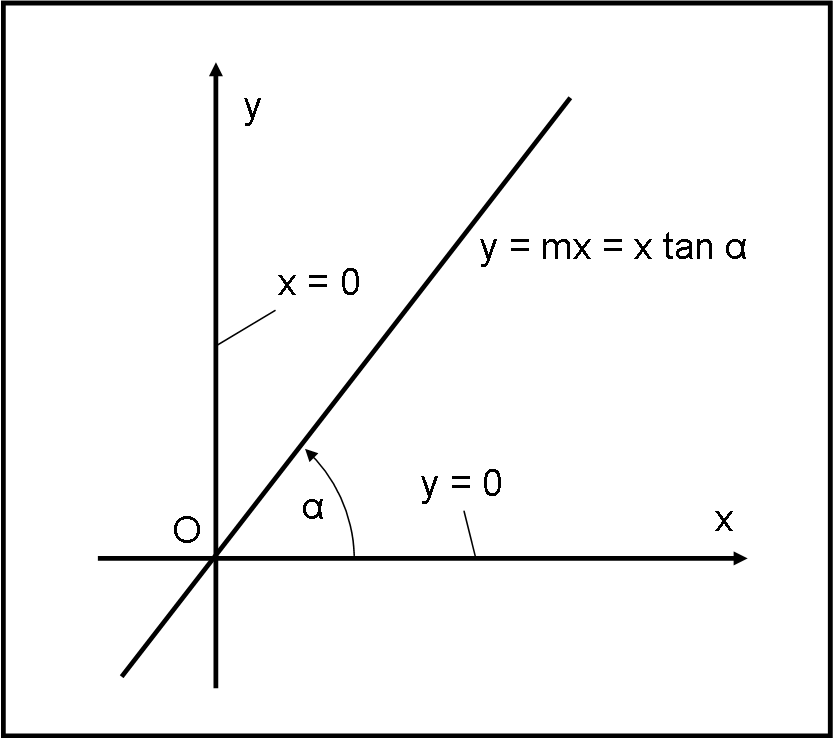
Cosa rappresenta l’asse x? proprio ciò che ho appena detto: il luogo dei punti del piano per cui la y è zero. In altre parole, l’asse x può essere scritto analiticamente come:

y = 0

Cosa rappresenta, invece, l’asse y? Banale! Il luogo dei punti del piano per cui la x è uguale a zero. In termini matematici:

x = 0

Queste sono le equazioni dei due assi. Una retta passante per l’origine ha equazione:

y = mx = x tan α

Facciamo allora la stessa cosa per determinare le equazioni degli assi x’ e T’ nel sistema x e T.

Come possiamo definire l’asse T’. Facile… il luogo dei punti che hanno x’ = 0. Ma cosa significa porre x’ = 0 nella trasformazione di Lorentz?

x’ = (x – βT)/(1 – β²)^1/2 = 0

Escludendo, per adesso, il caso in cui β = 1, che porterebbe il denominatore a zero, la relazione precedente diventa:

x’ = x – βT = 0

In semplici parole, dire che la x’ è uguale a zero (ossia descrivere l’asse T’) vuole anche dire:

x – βT = 0

o, anche:

T = 1/β x

Questa non è altro che l’equazione di una retta con coefficiente angolare c/v. Essa descrive il nuovo asse T’ nel sistema di riferimento (x,T).

Dire che il coefficiente angolare è uguale a c/v, vuole anche dire che l’angolo α che la retta forma con l’asse x è tale che:

tan α = c/v

L’asse T’ non può quindi descrivere qualsiasi retta. Per α = 90°, abbiamo che c/v = ∞, ossia v = 0. L’asse T’ coincide con l’asse T. D’altra parte la faccenda è ovvia, dato che se v = 0 il nuovo sistema non si muove e quindi non subisce nessuna trasformazione!

Per α = 45°, la retta diventa T = x, ossia v = c. Questo è il massimo valore che può raggiungere la velocità v e non è ammissibile avere angoli minori di 45° che vorrebbero dire velocità v maggiori di c.

Cerchiamo, adesso, l’asse x’. Esso deve essere definito, ponendo:

T’ = (T – βx)/(1 – β²)^1/2 = 0

Ossia

T – βx = 0

E, ancora:

T = βx

Anche questa è una retta nel sistema x,T e ha coefficiente angolare  β = v/c, ossia:

tan ϑ = v/c

Questa retta diventa l’asse delle x (T = 0) per v/c = 0 ossia per v = 0. Per v/c = 1 (valore limite) essa diventa nuovamente T = x, ossia coincide con l’asse delle T’.

In generale, abbiamo trovato che:

tan α = c/v

e

tan ϑ = v/c

ossia:

tan α = 1/ tan ϑ

ricordando che, per un angolo qualsiasi φ, vale la relazione:

tan (90 – φ) = 1/tan φ

Possiamo concludere che:

α = 90 – ϑ

Le due rette T’ e x’ sono, perciò, inclinate dello stesso angolo ϑ rispetto all’asse delle T e delle x, rispettivamente. Esse coincidono per ϑ = 45°, ossia per v =c.

Più di tante parole, vale la Fig. 2 che mostra i due nuovi assi T’ e x’ ottenuti attraverso la trasformazione di Lorentz e disegnati nel sistema considerato fermo (T,x). Qualcosa di nettamente diverso dal piano galileiano che aveva l’asse t sempre uguale a se stesso.

Ripetiamo, ancora, quanto trovato: la trasformazione di Lorentz trasforma un sistema con assi ortogonali in un sistema con assi non più ortogonali.

Ottenuto il nuovo sistema S’ (che è in movimento rispetto a S) è immediato definire le coordinate di un punto nel nuovo sistema. In realtà, essendo ormai in uno spaziotempo a tutti gli effetti, il “punto” dovrebbe sempre essere indicato come “evento”. Se ogni tanto ci “scapperà” il nome “punto”, ricordiamoci sempre del suo nuovo significato.

Come facevamo a determinare le coordinate di un punto P nel sistema x,y ? Si tracciava da P la parallela all’asse x e l’intersezione con l’asse y ci dava l’ordinata y del punto P. Analogamente, si tracciava da P la parallela all’asse y e la sua intersezione con l’asse x ci dava l’ascissa x. Lo abbiamo fatto centinaia di volte, quasi senza pensarci, come mostrato in Fig. 3.

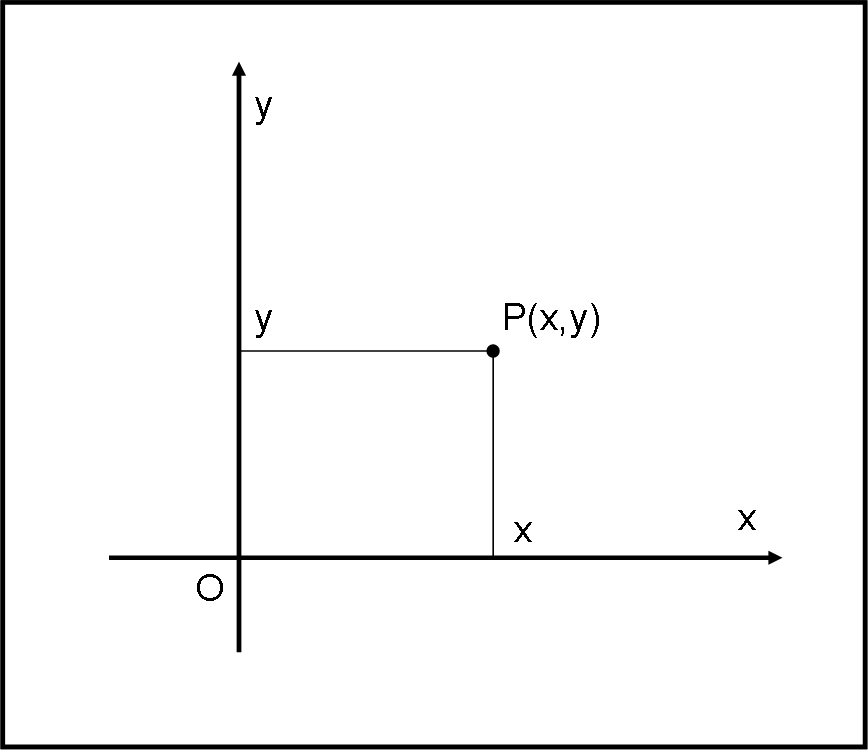
Per determinare le coordinate di un evento P nel nuovo sistema S’, di assi x’ e T’, non ci resta che fare lo stesso. Dall’evento P si traccia la parallela all’asse x’ e la sua intersezione con l’asse T’ ci dà il valore di T’. Analogamente, la parallela tracciata da P all’asse T’ incontra l’asse x’ in x’. Un gioco da bambini, mostrato in Fig. 4. Nella stessa figura abbiamo anche inserito le coordinate (T,x) dell’evento nel sistema S.

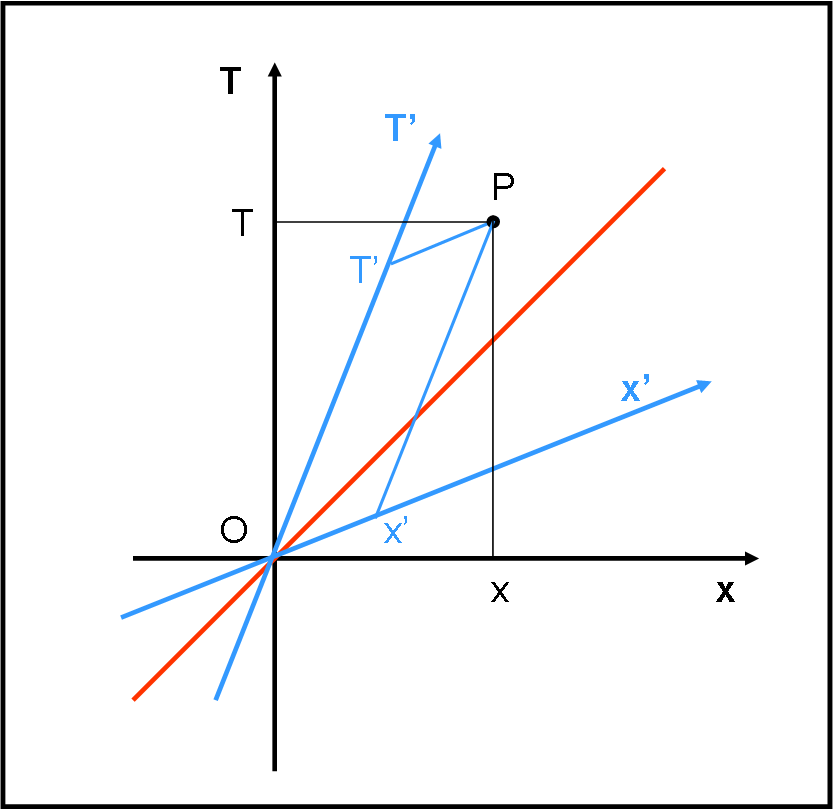
Sembrerebbe di avere concluso ben poco… ma, pensiamo un attimo alle conseguenze che questa trasformazione ha causato passando da un sistema a un altro o -ancor meglio- guardando dal primo sistema ciò che capita nel secondo. Non voglio anticipare troppo, dato che toccheremo i vari punti con estrema calma. Tuttavia, cominciate a pensare al concetto di simultaneità. L’evento P è simultaneo a tutti gli eventi posti sul segmento nero PT nel sistema S(T,x) ma è simultaneo a tutti gli eventi posti sul segmento blu PT’ nel sistema S’(T’,x’). Già questo  ci trasporta immediatamente al concetto di relatività della simultaneità…