Relatività Ristretta Rivista. 3bis(1). Ancora sulla simultaneità *
Sempre per cercare di semplificare al massimo il concetto di simultaneità relativa proviamo a eseguire un esercizio di estrema semplicità e -probabilmente- ancora più intuitivo. Notiamo ancora una volta che tutto ciò serve a evidenziare come due eventi che sono simultanei in un sistema di riferimento non lo sono più in un altro, se i due sistemi sono in moto relativo. Non vogliamo fare niente di più (per adesso). Teoricamente, la problematica sarebbe più che sufficiente per rendersi conto della dilatazione dei tempi e della contrazione delle lunghezze, ma -al momento- non pensiamoci, dato che è molto più conveniente digerire bene alcuni passi successivi.
Se vogliamo capire la rappresentazione grafica della RR è necessario andare per gradi, senza cercare di estrapolare il discorso. Accontentiamoci di digerire apparenti banalità e restiamo legati all’esperimento che eseguiamo.
Consideriamo un sistema di riferimento S’, che disegniamo in rosso, dato che sarà quello che metteremo in moto. Per chi vive su quel sistema, tuttavia, il movimento proprio non esiste. Lui si sente SEMPRE immobile. Cerchiamo di capire esattamente cosa vuol dire questa frase: non esiste nessun esperimento fisico eseguibile su un sistema di riferimento che possa far capire a chi ci vive se è in moto oppure se è fermo. Questo concetto non è altro che la relatività galileiana che viene ripresa pari pari da Einstein, espandendo “ fenomeno meccanico” a “ fenomeno fisico”. Tutto ciò è stato analizzato in dettaglio negli articoli sulla RR.
Il sistema S’ è molto semplice. Vi è una lampadina in A’ e uno specchietto in B’. Ovviamente, gli orologi sono stati sincronizzati con il solito sistema. Ne usiamo uno solo (quello in A’) dato che è più che sufficiente. Misuriamo con un asta rigida la distanza L’ = A’B’ che si mantiene , ovviamente, sempre uguale.
Disegniamo la Fig. 1. In basso a sinistra, nel riquadro nero, vi è il nostro sistema S’. Al tempo t’0 accendiamo la lampadina in A’. Nella parte sinistra della figura, la luce inizia a viaggiare verso B’ e lo raggiunge al tempo t’1. Possiamo essere sicuri che l’orologio in A’ segna lo stesso tempo di B’, ma non c’importa più di tanto, per adesso. Allo stesso tempo t’1 la luce viene riflessa e inizia a tornare indietro verso A’. Torna al punto di partenza al tempo t’2. La distanza A’B’ è sempre la stessa e la velocità della luce c anche. Se ne deriva, senza tanti problemi, che il tempo t’1 deve essere equidistante da t’0 e da t’2, dato che t’1 – t’0 = L’/c = t’2 – t’1.
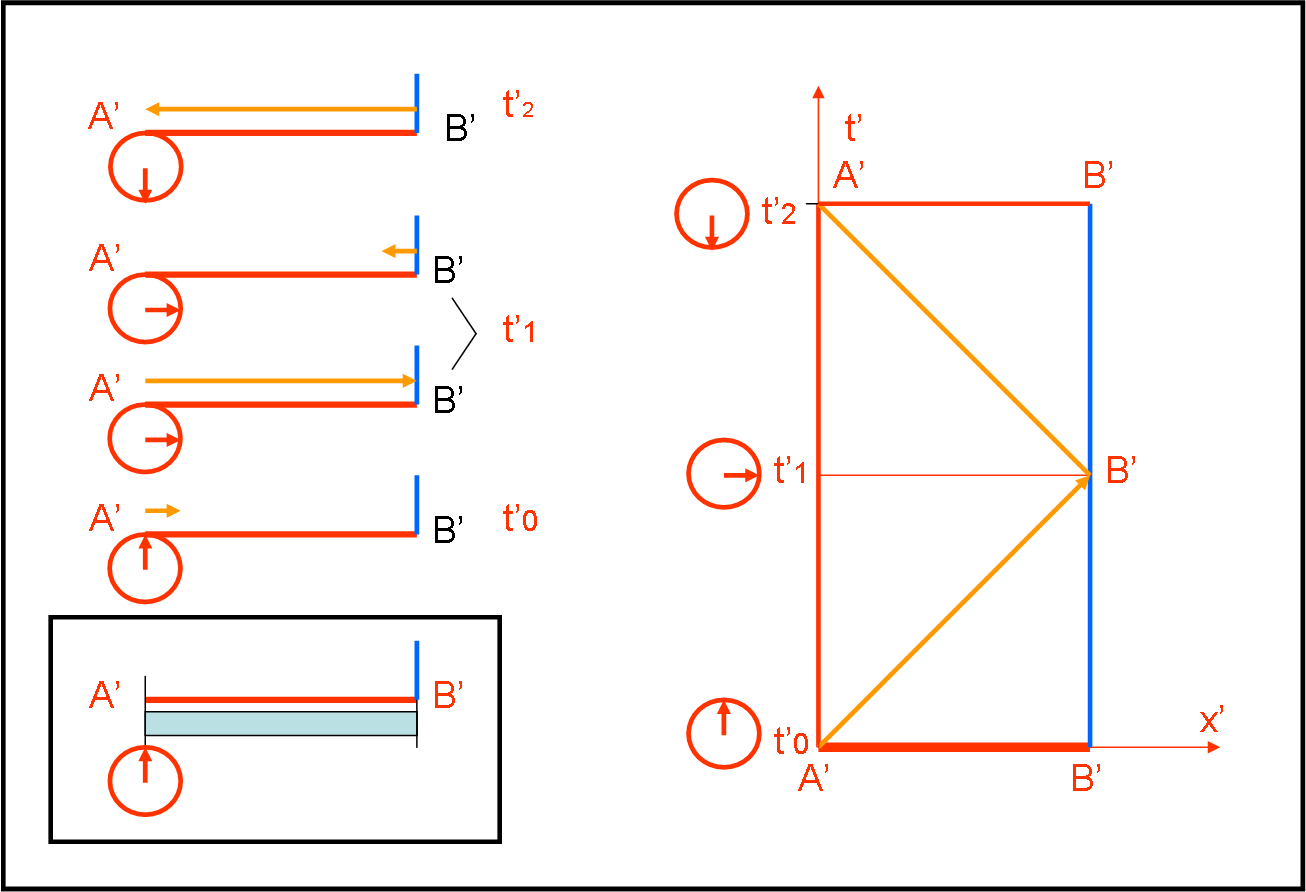
Abbiamo solo usato la costanza della velocità della luce e la costanza di L’. La velocità è uguale a una differenza di spazio divisa una differenza di tempo. Se la velocità è costante e la differenza di spazio (L’) è costante, lo deve essere anche la differenza di tempo.
La figura ci fa capire molto bene la differenza tra punto ed evento. A’ e B’ sono punti fissi del sistema S’, che vengono definiti solo dalla loro coordinata x’. A’(t’0), A’(t’1), A’(t’2) e B’(t’0), B’(t’1), B’(t’2) sono invece eventi a cui vanno incontro i punti A’ e B’. Due punti danno luogo a infiniti eventi. Anche questo concetto va inteso perfettamente prima di andare avanti.
Nel diagramma che andiamo a disegnare i punti si muovono, ma teniamo presente MOLTO bene che tipo di movimento. Essi non cambiano mai la loro coordinata spaziale, mentre cambiano la loro coordinata temporale.
Sappiamo già come fare a disegnare in modo più quantitativo l’esperimento appena fatto e lo descriviamo nella parte destra della figura. L’asse x’ è l’asse dello spazio dove vengono identificati in due punti A’ e B’. Questa situazione vale, però, solo per l’istante t’0. Nel diagramma, quindi, A’ e B’, posti sull’asse x’, rappresentano due eventi. Allo scorrere del tempo gli eventi si spostano verso l’alto, così come si sposta verso l’alto l’asse dello spazio (ossia l’asse del sistema fisico S’) che contiene i punti fissi. In ogni istante l’asse che definisce il sistema S’ si muove solidalmente in funzione del tempo.
Non confondiamo l’asse spaziale istantaneo del sistema in continuo movimento in funzione del tempo, con un asse di riferimento che vogliamo considerare fisso e che disegniamo quando il tempo è, per esempio, posto uguale a zero. L’asse x’ del sistema di coordinate è quindi uno qualsiasi degli assi istantanei che contengono i punti A’ e B’. Nel disegno che stiamo eseguendo questo asse considerato fisso è quello relativo all’istante t’0 (ma potevamo usarne un altro a piacere). Ci serve solo come riferimento per potere quantificare le grandezze che cambiano in funzione del tempo.
Cosa succede, allora, al nostro sistema S’ composto da A’, con la lampadina, e B’, con lo specchietto? Si sposta verso l’alto rispetto all’asse rappresentato come fisso (quello relativo al tempo t0’). Il movimento mantiene la distanza L’ e la sincronizzazione degli orologi, ossia in ogni istante una retta t’ = cost, deve contenere sia A’ che B’. Questo fatto ci dice che gli orologi in A’ e in B’, che stanno su una retta del genere, segnano sempre lo stesso tempo. Come possiamo esprimere questa situazione usando altre parole? Facile: gli eventi A’ e B’ che stanno su una parallela all’asse x’ sono simultanei! Lo sono, dato che avvengono allo stesso istante.
Vale, però anche il viceversa: se due eventi sono simultanei,devono ovviamente stare su una retta parallela a quella della coordinata spazio x’. Ricordiamoci bene questo punto, dato che non è detto che questa retta sia sempre orizzontale… così come non è detto che quella del tempo sia sempre verticale…
Bene, facciamo partire la luce da A’ al tempo t’0. Questa doppia definizione (posizione e tempo) identifica l’evento A’(t’0). La luce, però, non è legata al sistema S’, ossia un suo fotone è libero di percorrere un certo spazio in un certo intervallo di tempo. Come si muove, allora, nel diagramma di destra? Si muove secondo una retta inclinata, dato che la serie di eventi del fotone non mantengono la stessa posizione nel sistema di riferimento S’. Il fotone si muove spazialmente mentre si muove temporalmente. Ripetiamo: i punti A’ e B’ si muovono solo lungo l’asse del tempo, dato che sono FERMI nel loro sistema S’, descrivendo gli eventi che sono paralleli all’asse del tempo, mentre la luce percorre una traiettoria inclinata dato che al passare del tempo si sposta anche spazialmente lungo il sistema.
Scegliamo l’unità dell’asse del tempo in modo che la luce o –meglio- la retta che descrive i suoi eventi sia inclinata proprio di 45°. Questa scelta l’abbiamo già discussa a fondo (ma ci torneremo). Quello che sta succedendo (nella realtà del nostro mondo spaziale) è esattamente ciò che capita nella parte di sinistra della figura. La luce parte da A’, scorre lungo l’asta rigida e va a colpire lo specchietto in B’. Nel diagramma a destra questa parte è quella compresa tra t’0 e t’1. E’ sicuramente una banalità, ma cerchiamo di capire molto bene questa perfetta uguaglianza di situazione, altrimenti il diagramma di Minkowski ci apparirà solo come un guazzabuglio di linee…
Una volta che la luce tocca B’, quando si trova in t’1, è costretta a tornare indietro verso A’ a causa dello specchietto di B’. Inizia la fase di ritorno (parte alta della figura di sinistra). La luce torna indietro sempre lungo una traiettoria inclinata di 45°. Il percorso che deve compiere è esattamente quello dell’andata e quindi non può che giungere in A’ quando il tempo segna t’2. Come già detto precedentemente, la distanza temporale tra t’1 e t’0 deve essere uguale a quella t’2 e t’1.
Otteniamo un semplicissimo triangolo rettangolo isoscele. Isoscele, dato che i percorsi della luce (lati) devono essere uguali; rettangolo, dato che le due traiettorie sono entrambe inclinate di 45° rispetto all’asse x’ (o t’). La “base” del triangolo non è altro che il tempo totale impiegato dalla luce per andare e per tornare. Le due parti della figura sono perfettamente identiche: la prima ci dà una visione più qualitativa, ma più concreta rispetto alla realtà del mondo che ci circonda, la seconda ci dà una visione perfettamente quantitativa in un diagramma spaziotemporale!
Possiamo ancora notare, che, in un esperimento del genere, in qualsiasi sistema di riferimento venga disegnato, gli eventi A’ e B’, corrispondenti ai punti A’ e B’, devono essere sempre simultanei per qualsiasi valore del tempo t’. Ciò ci conferma ancora una volta, se ce ne fosse bisogno, che l’arrivo della luce in B’ al tempo t’1 è simultaneo con l’ evento (A’(t’1)) e questo evento è equidistante temporalmente da A’(t’0) e da A’(t’2). Ci è quindi bastato un solo orologio.
Fermiamoci qui, anche se abbiamo detto cose dall’apparenza ultra ovvie. Tuttavia, leggiamo e rileggiamo questo articolo e riflettiamo bene sulla figura altrettanto banale. Solo se non ci saranno più dubbi, si può veramente andare avanti.
Chi ha dubbi, perciò, li esprima subito, senza alcuna paura…






18 commenti
Perfetto Enzo vediamo se riesco a spiegare con mie parole il concetto di simultaneità.
La simultaneità è relativa al sistema di riferimento, mi spiego meglio, esempio di due eventi (esplosione di due supernove A-B) a me osservatore se la luce dell'esplosione mi arriva contemporaneamente da entrambe vuol dire che l'evento è simultaneo però al mio sistema di riferimento che è statico perchè vedo la luce di entrambe nello stesso istante vuol dire che sono fermo non mi muovo.
Ma se per esempio mentre è in atto l'evento (esplosione di due supernove A-B) sto viaggiando a velocità prossime a quelle della luce verso B vedro prima la luce di B e quindi i due eventi per me che sono in movimento non saranno più simultanei ma risulterà prima quello della direzione in cui sto viaggiando cioè B.
Se la velocità della luce è costante io non posso sommare la mia velocità a quella che mi arriva dall'esplosione viaggiando in direzione dell'evento.
ma allora perchè vedo prima l'esplosione in B?
Perchè non è la velocità a cambiare ma è il tempo che si dilata e le distanze si contraggono perciò viaggiando verso B a velocità molto elevate vedo prima B di A non perchè viaggio più veloce della luce ricordiamoci gli esperimenti fatti LA VELOCITA' DELLA LUCE NON E' INFINITA MA E' FINITA COSTANTE (300000 kms).
Succede invece che più viaggio veloce più le distanze si "contraggono" e di conseguenza il tempo si "dilata".
Va bon questo un esempio per esprimere quello che ho appreso Enzo mi dirà se ho toppato o meno.
Se mi è permesso vorrei porre all'attenzione di Vincenzo un'idea che da un po' mi ronza in testa ho letto che i satelliti GPS risentono del fenomeno della contrazione delle lunghezze e della dilatazione dei tempi che li portano ad errori anche di diversi km e devono essere costantemente ricalibrati mi piacerebbe che magari più avanti se ne parlasse naturalmente facendo uso dei diagrammi di Minkowsky magari più avanti certamente lascio a te Enzo a tua discrezione il dove il come ed il quando, credo possa essere interessante discutere di un fenomeno provato effettivo che attesta la veridicità degli effetti dell RR.
Volevo chiarire che quanto detto all'inizio che mi è sfuggito io come osservatore mi trovo esattamente a metà strada dalle due supernove quindi esattamente equidistante dagli eventi ci tenevo a precisare.
Caro Enzo, raccolgo l'invito a leggere questo articolo e provare a descrivere il mio opinabile e personale (e spero corretto ) approccio alle questioni trattate.
) approccio alle questioni trattate.
Vorrei provare a descrivere quello che a me è sembrato il modo più semplice per trovare velocemente gli assi t' e x' del sistema in movimento (treno) visto da un sistema che si considera fermo (marciapede).
Innanzitutto è meglio sfatare alcune dicerie che descrivono inenarrabili comportamenti del tempo e dello spazio nel sistema in movimento, anche se questo si muove a velocità costante .
.
L'esempio proposto è semplicissimo (lo stesso di questo articolo), serve solo un marciapede di una stazione ed un treno capace di muoversi in maniera costante a velocità prossime a quelle della luce.
Il marciapede nelle figure è un segmento di colore rosso, dal suo bordo sinistro (A) parte la luce, l'omino rosso (C) ha uno specchio che riflette la luce e la rimanda in A.
Il treno è un segmento blu, dal suo bordo sinistro (A') parte la luce, l'omino nero (C') ha uno specchio che riflette la luce e la rimanda in A'.
La figura descrive cosa vede l'osservatore fermo sul marciapiede e cosa vede il passeggero del treno dall'interno del vagone.
http://www.astrobin.com/full/34211/K/
Entrambi vedono esattamente la stessa cosa, la luce si comporta proprio come ci si aspetta.
Per l'osservatore sul marciapiede la luce parte da A0, viene riflessa in C2 e torna in A4 (ovviamente impiega lo stesso tempo per arrivare allo specchio e tornare indietro).
Per il passeggero del treno la luce parte da A'0, viene riflessa in C'2 e torna in A' 4. Anche in questo caso impiega lo stesso tempo per arrivare allo specchio e tornare indietro, ma attenzione che l'asse del tempo è quello del suo sistema di riferimento ossia t' (e non t).
Per il passeggero, qualunque sia la velocità del treno (purchè costante) non può certo cambiare la sua distanza dal bordo sinistro del vagone (C'-A'), ma attenzione che questa viene misurata sull'asse X' (e non X).
Per cui per il passeggero i bordi del vagone sono fermi, si muovono solo nel tempo, ma non nello spazio.
Non è poi così strano che il passeggero si possa considerare fermo. Ammettiamo che l'omino nero (passeggero sul treno) sia nato su quel treno e che questo non si sia mai fermato, viaggiando sempre alla stessa velocità costante.
Per lui, osservando dal finestrino, è il paesaggio che si muove a velocità costante, è il marciapiede che si allontana inesorabilmente da lui (se può sembrare un esempio estremo, la terra su cui poggiamo i piedi non è certo immobile nello spazio...).
Prima di descrivere le prossime due figure, è meglio evidenziare che gli eventi A e C si muovono solo nel tempo, per cui unendo tutti gli eventi A posso disegnare l'asse del tempo t e lo stesso discorso si può fare unendo gli eventi A', che si muovono lungo l'asse t' (il tempo nel sistema di riferimento del treno).
A questo punto non resta che analizzare nuovamente cosa succede al treno (sistema in movimento) visto però dal marciapede (sistema fermo)
Il treno (segmento blu) in un certo istante (to = t'o), coincide esattamente con il marciapiede (segmento rosso), ossia Ao = Ao' e Co=C'o, in tale istante sia Ao sia A'o accendono le loro lampadine.
Basta far muovere nello spazio, oltre che nel tempo, il treno (segmento blu) e congiungere tutti gli eventi A', che come ricavato prima descrivono proprio l'asse del tempo t' (vedi figura precedente)..... in un attimo è possibile disegnare nel sistema fermo l'asse del tempo t' e le sue rette parallele (come quella su cui si sposta l'evento C')
(come quella su cui si sposta l'evento C')
http://www.astrobin.com/full/34211/L/
La luce, per qualunque sistema di riferimento viaggia sempre alla sua solita velocità, per cui deve essere rappresentata con rette inclinate di 45° (impiega 1 anno di tempo per percorrere 1 anno luce di spazio).
La luce riflessa dall'omino rosso (linea verde, parte da Ao arriva in C2 e torna in A4) si comporta come al solito (d'altronde il sistema di riferimento usato è proprio il suo), mentre vista dal marciapiede la luce riflessa dall'omino nero (sul treno), compie un percorso ben diverso.
La luce partita da A'o (insieme a quella partita da Ao) arriva in C'4 e torna in A'5.
Dato che nell'istante to=t'o, Ao coincideva con Ao' e Co con C'o (i segmenti rossi e blu erano sovrapposti) la luce dovrebbe impiegare lo stesso tempo per andare da A a C e tornare in A e per andare da A' a C' e tornare in A', quindi il tempo misurato dal marciapiede non può essere lo stesso di quello misurato dal treno.
Perciò ciò che appare simultaneo se visto dal proprio sistema di riferimento non lo è più se visto da un altro.
Quindi gli eventi A4 (luce che torna in A dopo esser stata riflessa da C) ed A'5 (luce che torna in A' dopo esser stata riflessa da C') dovrebbero accadere simultaneamente, ossia unendo questi due eventi è possibile tracciare la linea di simultaneità.
http://www.astrobin.com/full/34211/M/
Per disegnare l'asse X' basta tracciare una retta passante per l'origine degli assi, parallela alla linea di simultaneità trovata.
Dato che l'asse X' passa per C'1, sono abbastanza convinto che il ragionamento funzioni.
L'ultimissima illustrazione (che trovo interessante per alcune figure geometriche che intravedo) si limita volutamente a mostrare solo alcuni eventi simultanei...... sarebbe interessante dimostrare insieme perchè sono simultanei.
http://www.astrobin.com/full/34211/N/
A proposito, a mio avviso, il punto C'1 può risultare utile per trovare la linea di simultaneità usando un altro approccio.. ma l'ho già fatta troppo lunga...
Paolo
In fisica la contrazione delle lunghezze, in accordo con la teoria della relatività ristretta è un fenomeno fisico che si manifesta nella riduzione delle lunghezze, riconosciuto da un osservatore in oggetti che viaggiano a qualsiasi velocità relativa allo stesso (purché diversa da zero).

Queste contrazioni diventano comunque rilevanti solo a frazioni significative della velocità della luce e la contrazione è soltanto nella direzione parallela alla direzione verso cui l'oggetto osservato si muove.
La Terra che si muove a circa 30 km/s, ha una CONTRAZIONE che risulta essere circa di una parte su 200.000.000, che si traduce in circa 6 cm sul diametro della Terra. Questo piccolo cambiamento dà ragione del risultato negativo dell'esperimento di Michelson e Morley, comportando che la sorgente della luce e lo specchio fossero più vicini quando questi erano disposti lungo la direzione del moto della Terra.
Che inenarrabile comportamento
caro Foscoul,
parleremo sicuramente del gps e dell'effetto doppler che in qualche modo hai descritto...
Tempo al tempo.
Caro Paolo,
concordo con te che una figura del genere dà luogo a molte interpretazioni e i segmenti usati portano quasi tutti alla stessa conclusione. Tuttavia, non mi trovo molto s'accordo sull'utilizzo dei due eventi finali... Uno si riferisce a un sistema e l'altro a un altro sistema. Una linea di simultaneità deve collegare eventi istantanei nello stesso sistema... Non rischiamo di trovare risultati anche corretti graficamente ma che non abbiano una consistenza fisica. Sempre che abbia capito bene le tue figure...
Mi spiego meglio Paolo...
da come lavora il diagramma risulta giusto ciò che dici tu, nel senso che il tempo deve essere uguale, ma non possiamo mischiare i due sistemi per trovare una linea di simultaneità. La simultaneità deve essere riferita a ciascun sistema. Ossia deve essere tale che il tempo t o t' siano costanti. la linea A4 - A'5 unisce eventi relativi a due sistemi di riferimento... è decisamente più corretto unire eventi dello stesso sistema di riferimento che siano simultanei per trovare una linea che appartiene a un dato sistema. Ad esempio l'evento al tempo mediano lungo la retta A'1-A'5 e l'evento C'4...
Scusa, non voglio fare il pignolo, ma è meglio non mischiare situazioni che potrebbero confondere... O, almeno, è una mia visione personale....
Grazie Enzo sei gentilissimo e sempre disponibile.
Certamente ho descritto (alla mia maniera) l'effetto doppler ma quello Relativistico naturalmente.
l'effetto doppler ma quello Relativistico naturalmente.
Comunque grazie ancora Enzo pian piano grazie a te si cresce.
Caro Enzo hai ragione ad esser pignolo su come ho trovato la linea di simultaneità così si rischia di fare confusione mischiando eventi di sistemi diversi.
Forse è meglio un altro approccio.
Nelle prime figure, quelle in cui ognuno vedeva cosa succedeva dal proprio sistema di riferimento, unendo gli eventi A' si otteneva l'asse del tempo t' (dato che A' visto dall'interno del treno si muove solo nel tempo).
Qual'era la linea di simultaneità?
Quella che univa A' a C' (per il marciapiede A e C) in ogni istante di tempo.
Ossia: A'0=C'0; A'1 = C'1; A'2= C'2, ecc.
Nella rappresentazione del treno in movimento nel sistema fermo (marciapiede) dove si trovano A' e C' nello stesso istante di tempo (t')?
La luce dovrebbe impiegare lo stesso tempo per andare da A' a C' e per tornare da C' ad A' (il viaggiatore sul treno è sicuro di questo, come visto nelle prime due figure).
L'evento intermedio tra la posizione di partenza della luce (A'0) e il suo ritorno (A'5) corrisponde all'evento A'3.
Dato che Δt'1=Δt'2, quando la luce ha percorso metà strada, il bordo sinistro del treno si trova in A'3 (ossia una posizione temporale intermedia di A' misurata sull'asse t').
Nella rappresentazione del treno in movimento visto dal sistema fermo (marciapiede), non vi è alcun dubbio che la luce per tornare in A'5, deve essere stata riflessa dall'omino nero in C'4.
Ma C'4 dovrebbe trovarsi a metà del percorso della luce, per cui quando il bordo sinistro del treno si trova in A'3 (metà percorso luce), C' si trova in C'4.
Unendo questi due eventi simultanei si ottiene la linea di simultaneità
http://www.astrobin.com/full/34211/O/
In ultimo, una inusuale rappresentazione del treno in movimento rappresentato nel sistema fermo
http://www.astrobin.com/full/34211/P/
Così va meglio?
Paolo
mooolto meglio!
Aggiungo solo una figura che consente di tracciare come linea di simultaneità direttamente l'asse X'.
http://www.astrobin.com/full/34211/Q/
Il ragionamento è lo stesso di prima.
Nel movimento di C' lungo l'asse del tempo t' (retta parallela all'asse t') c'è una sola posizione che consente alla luce di raggiungere A'3 (e tra l'altro anche A4) e questo evento è C'1 (linea tratteggiata gialla).
La luce che parte da A', per raggiungere C'1 deve necessariamente partire da A'-2.
L'evento A0 rappresenta proprio la posizione mediana tra A'-2 e A'3 (Δt’1=Δt’2 )
Se il bordo sinistro del treno di trova in A'0 (metà tempo percorso luce, ossia A'-C'), l'omino nero che riflette la luce che arriva in A'3 si trova in C'1.
Quindi A'0 e C'1 sono eventi simultanei.
Dato che A'0 coincide con l'origine degli assi, la retta che congiunge A'0 a C'1 è proprio l'asse X'.
Paolo
caro Paolo,
è più o meno quello che era stato prospettato come quiz un po' di tempo fa... ricordi?
Certo che mi ricordo del quiz
http://www.infinitoteatrodelcosmo.it/2015/04/16/quiz-antipasto-per-lo-spaziotempo-di-minkowski/
E' quello in cui sta povera linea di simultaneità avevo provato a inserirla un pò ovunque, ma in posizione errate, solo alla fine sono arrivato alla soluzione
Paolo
Caro Enzo, così per divetimento, in attesa di seguire come affrontare il paradosso dei gemelli, ho provato a realizzare una figura per descrivere una situazione simile ad un astronave che parte si avvia verso una certa destinazione, inverte la rotta e torna a Terra (usando un esempio molto simile a quello precedente).
Ho preferito inserire qui il commento, poiché si è affrontata la questione.
La figura mostra la possibile rappresentazione .
rappresentazione .
http://www.astrobin.com/full/38888/B/
Il problema è che mentre per il sistema fermo la luce raggiunge A' nell'istante in cui l'astronave rientra a terra (A =A'), per il sistema in movimento la luce raggiunge A' (dopo la doppia riflessione) molto prima di tornare a Terra.
Quindi, visto dal sistema fermo la luce (due rimbalzi) raggiunge A' quando questo torna in A, visto dal sistema in movimento affinchè ciò possa accadere la seconda lampadina gialla dovrebbe accendersi più tardi lampadina rossa (c'è un evidente “salto” temporale in quell'inversione di marcia... o sbaglio? ).
).
http://www.astrobin.com/full/38888/C/
In ultimo, mostrando i segmenti rappresentati sui lori assi (linea di simultaneità), avendo posto un'inversione istantanea del moto, paradossalmente (visto dal sistema fermo) vi sono due eventi A1' che risultano simultanei rispetto a C1'.
http://www.astrobin.com/full/38888/D/
Da questa rappresentazione e dai problemi che suscita, a me sembra che c'è una bella differenza tra cosa accade al terricolo e ciò che accade all'astronauta.
Chi rimane a Terra non cambia mai sistema di riferimento, mentre l'astronauta passa da un sistema fermo (o meglio solidale con la Terra), ad un sistema in movimento con velocità positiva, poi ad un sistema in movimento con velocità negativa, infine ad un sistema fermo (la Terra).
Paolo
caro Paolo,
hai affrontato il problema dei gemelli nel modo giusto e sei arrivato a "toccare" il punto chiave! Non vi è bisogno veramente di pensare al punto di mezzo C', ma tutto, comunque, torna a "bomba". La parte finale (il salto temporale) è la chiave di volta. A causa del cambiamento di sistema, il tempo "salta" e ne deriva il non invecchiamento REALE, univoco e non simmetrico. L'ideale sarebbe mettere come asse di riferimento la prima parte del moto dell'astronave (asse y) e disegnare cosa capita alla seconda parte del viaggio e alla Terra. Solo così si riesce a dimostrare che anche chi viaggia si rende conto di invecchiare di meno, senza passare alla RG. Tuttavia, per fare questa parte bisogna sapere comporre relativisticamente le velocità...
Comunque sei partito alla grande!
Aggiungo un piccolo commento. La figura riferita al sistema S' vede descritto ciò che capita alla luce nel sistema pensato fermo e quindi non può essere simmetrica all'altra. Temo che questo cambiamento abbia un po' confuso il problema... Oltretutto tu imponi tutto il viaggio lungo l'asse y, ma in realtà vi è un cambiamento di velocità anche per il viaggiatore, dato che torna indietro... La figura vista da S' non è corretta...
Caro Enzo, vediamo se ho capito l'errore di rappresentazione.
Se voglio tracciare il percorso della luce non posso ignorare che a un certo punto l'astronave inverte la rotta.
Se prendo come riferimento la prima parte del percorso assumendo che S' si muove solo nel tempo, ma non nello spazio, quando inverte il senso di marcia l'asse t' cambia (visto partendo dalla prima parte del percorso).
http://www.astrobin.com/full/38888/E/
Perciò ho inclinato l'asse t' nella seconda parte del percorso (ritorno)... l'inclinazione è la stessa con velocità -V e conseguentemente ho portato l'asse t in posizione vertcale, ossia ferma.
Ho pensato che se nella seconda parte del percorso si rappresenta l'astronave che si muove verso la Terra, questa risulti ferma in attesa di esser raggiunta (ma forse mi sbgalio..)
Forse così va meglio, fermo restando il problema del salto temporale di prima .
.
Paolo
caro Paolo,
il concetto è quello giusto... tuttavia, per disegnare nel sistema di riferimento della prima parte del viaggio la seconda parte non basta invertire la velocità (quella sarebbe la velocità della Terra), ma bisogna sommare due velocità, quella della terra e quella dell'astronave che si muove rispetto a lei. Cerco di spiegarmi, meglio: l'inversione di v la fai quando vedi la Terra vista dall'astronave. Ma in questo caso, devi tenere conto che nel ritorno vi è anche il moto dell'astronave visto da terra... insomma, a parole è difficile, ma è proprio QUI che si devono sommare delle velocità e le velocità NON si sommano come faceva Galileo, ma c'è una formula che tiene conto del fattore di Lorentz... Ne deriva che l'inclinazione del ritorno rispetto all'andata non è un semplice ribaltamento. Il semplice ribaltamento sarebbe quello della Terra vista dall'astronave, mentre qui devi disegnare l'astronave-ritorno vista dall'astronave- andata.