Iniziamo dalla parte più generale, ossia dai cosiddetti fenomeni superluminali, quelli in cui le velocità misurate di certi “oggetti”  raggiungono valori anche notevolmente superiori a quella della luce. Stiamo parlando di relatività speciale e la faccenda ci interessa particolarmente. Ne avevo già scritto anni fa, ma è meglio che riprenda quell’articolo e lo ripresenti come antipasto alla news. Anche se la soluzione appare, adesso, abbastanza ovvia, non possiamo dimenticare che queste osservazioni “apparentemente assurde” avevano creato non pochi problemi agli astrofisici. Stiamo, comunque, tranquilli: la “nostra” relatività speciale non subisce nessun contraccolpo.

In realtà, dai tempi di apparizione dell’articolo originale, sono stati fatti passi in avanti nella comprensione della matematica, della geometria e della fisica, da parte dei “nostri” lettori, per cui siamo ora in grado di illustrare il processo superluminale in due modi, uno puramente intuitivo e qualitativo e uno più quantitativo, che fa uso di poche formule. Nessun modello standard più o meno trasformato “ad hoc”, nessuna funzione iperbolica, nessuna materia oscura luminosa o materia luminosa oscura e nemmeno strane curvature temporali… solo una buona comprensione dei fenomeni fisici in gioco, che sono ormai alla portata di tutti i magnifici lettori del “circolo”. Chi ha le basi fondamentali può arrivare ovunque!

Fenomeni superluminali

1. Descrizione qualitativa

Questi fenomeni prendono il nome di sorgenti superluminali, in quanto sembrano propagarsi a velocità di gran lunga superiori a quella della luce. Normalmente sono associati a galassie attive e si formano a causa della caduta di materiale verso il buco nero centrale. Si presentano normalmente come getti di particelle che vengono scagliate verso lo spazio. Al loro interno si notano “nodi” più densi e luminosi che permettono di misurarne la velocità, dato che sono segni che possono essere seguiti col telescopio durante un periodo relativamente breve. Misurando lo spazio percorso da questi nell’unità di tempo si determina la velocità della materia del getto. Questo semplice “calcolo” può portare a velocità nettamente superiori a quella della luce, da cui il nome di sorgenti superluminali.

Come si è detto fin dall’inizio questi valori assurdi per la fisica odierna derivano da un fenomeno prospettico non molto difficile da descrivere, che si può spiegare in modo semplificato e abbastanza intuitivo…

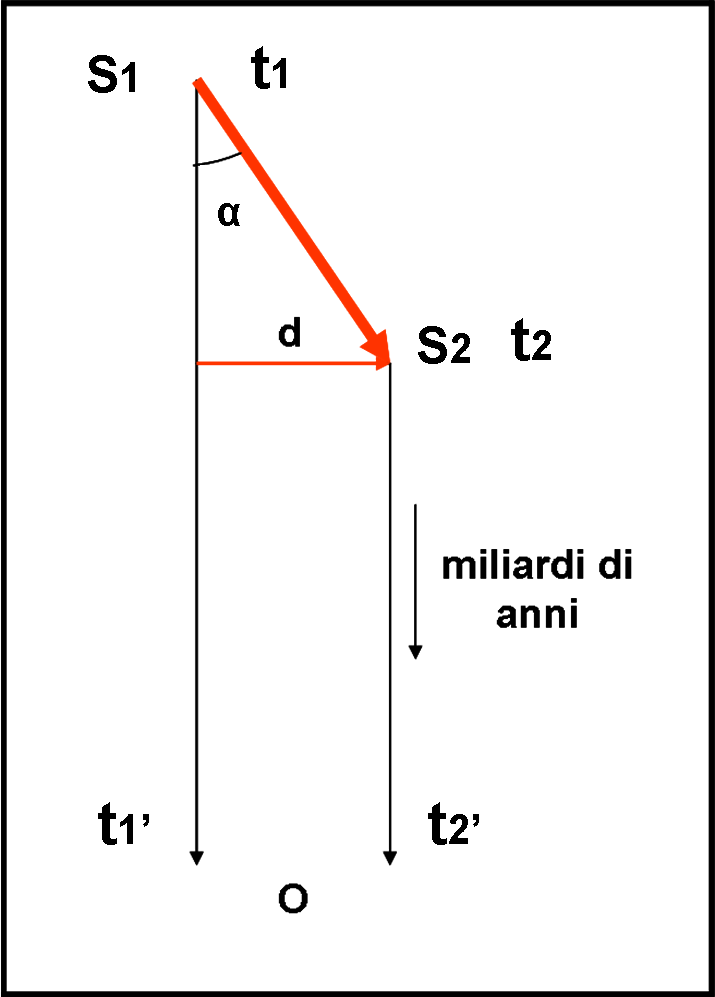
Consideriamo la Fig.1 in cui S₁ è  la sorgente all'interno del getto. Ammettiamo, per adesso, che la direzione del getto sia esattamente trasversale rispetto all’osservatore. Al tempo t₁’ osservo la luce del nodo partita al tempo t₁ (la differenza tra questi tempi dipende ovviamente dalla distanza della sorgente da noi e potrebbe anche essere di miliardi di anni, ma  poco importa). Al tempo t₂ il nodo si è spostato in S₂ e la sua luce giunge sulla Terra al tempo t₂’. Per percorrere il tratto S₁S₂ = d  nel tempo t₂ – t₁ il nodo ha viaggiato al velocità v = d/(t₂ – t₁). Questa è la velocità reale del getto e non può ovviamente superare quella della luce. Tuttavia, le si avvicina molto e questo è estremamente importante.

L’osservatore misura, ovviamente, la differenza di tempo (t₂’- t₁’) e la distanza d. Nella situazione rappresentata nella Fig. 1, la differenza t₂’ – t₁’ risulta perfettamente uguale a t₂ – t₁. Notiamo che per i valori estremamente piccoli dell’intervallo di tempo e della distanza percorsa possiamo trascurare completamente gli effetti dovuti all’espansione dell’Universo (lo spazio si espande ma non i singoli oggetti e il getto può considerarsi proprio come un singolo oggetto).

Se vogliamo calcolare la velocità osservata da terra dobbiamo fare v’ = d/(t₂’- t₁’), che è uguale a quella vera v = d/(t₂ – t₁), dato che t₂ – t₁ = t₂’- t₁’. La velocità misurata è altissima ma non va contro la teoria della relatività.

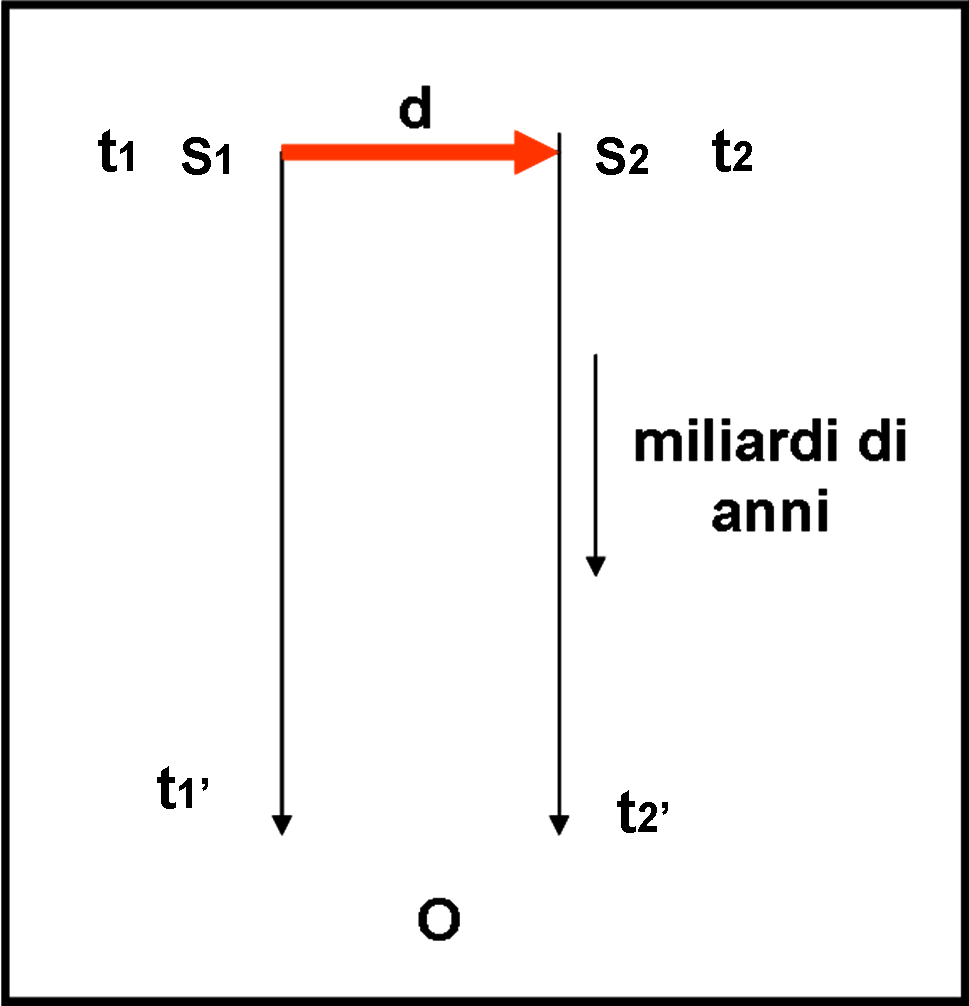
Non siamo, pero, sempre così fortunati… Consideriamo la Fig. 2, dove il getto è inclinato e forma un angolo α, abbastanza piccolo, con la linea di vista. Noi, ovviamente non possiamo sapere la configurazione effettiva della sorgente e del suo getto e dobbiamo limitarci a eseguire i calcoli basandoci su quello che vediamo, che, in questo caso, è una proiezione,  sulla sfera celeste, di quanto capita realmente . Possiamo, oltretutto, calcolare solo i tempi di arrivo sulla Terra della luce del nodo durante il suo percorso.

La distanza d misurata è esattamente uguale a quella precedente (anche se non possiamo sapere se è una proiezione o è quella effettiva). Misuriamo nuovamente la differenza osservata tra i tempi  t₂’ e t₁’. Con grande meraviglia troviamo che  v = d/(t₂’– t₁’) supera di gran lunga la velocità della luce.

Dov’è l’errore?

Stiamo bene attenti… il calcolo che abbiamo fatto presuppone che le condizioni effettive siano come quelle del caso fortunato della Fig.1. D’altra parte, da terra, non possiamo fare altro. Siamo, quindi, costretti a considerare t₂’– t₁’ uguale a t₂ – t₁, ossia a considerare la differenza di tempo tra S₂ e S₁ come nel caso precedente.  E qui commettiamo l’errore fondamentale.

La differenza effettiva di tempo tra gli eventi REALI  S₂ e S₁ è ben maggiore di t₂’ – t₁’. Infatti, la luce che è arrivata da noi al tempo t₁’, relativa alla sorgente in S₁, è partita ben prima (t1) di quanto rappresentato in Fig. 1. Essa ha dovuto percorrere un tratto decisamente più lungo rispetto a quella che ha percorso S₂. Per trovare la vera velocità del getto dovremmo dividere la distanza per un tempo molto più lungo (che non possiamo conoscere).

Siamo, perciò, costretti a dividere per un valore più piccolo, che rispetto a quello vero decresce al diminuire dell’angolo α. Dividendo una distanza costante per un tempo sempre più corto rispetto a quello effettivo, troviamo una velocità sempre più grande che può tranquillamente superare di molto quella della luce, dato che la velocità reale è solo di poco inferiore.

2. Descrizione quantitativa

Supponiamo che dal buco nero BN venga emesso un getto di particelle verso l’osservatore lungo una direzione che forma un angolo α con la linea di vista (Fig. 3). Supponiamo inoltre che il nodo, visibile, si muova con una velocità v,  vicina alla velocità della luce c .

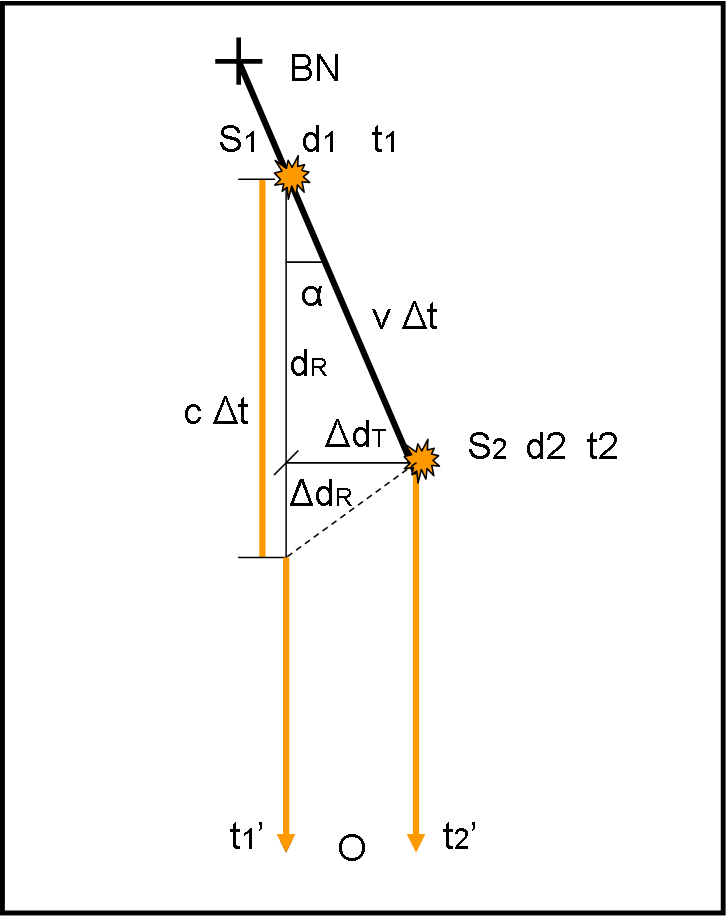
Siano d₁ e d₂ = d₁+ Δd = d₁ + vΔt, le distanze delle posizioni S₁ e S₂ del nodo rispetto al buco nero BN in due istanti  t₁ e t₂ = t₁ + Δt, rispettivamente. In queste due posizioni il nodo emette la propria luce. Nel passare da S₁ a S₂ , il nodo si avvicina all’osservatore, per effetto della sua velocità, di una quantità:

d_R = v cos(α) Δt

La luce emessa in direzione dell’osservatore quando era in S₁ ha già compiuto nel frattempo un tratto più lungo, pari c Δt .  Esiste, quindi, una differenza tra il tragitto percorso dalla luce verso di noi e quello percorso dal nodo. Quando il nodo arriva in S₂, ed emette la sua luce, quella inviata da S₁ è più a vicina a noi (c > v). La loro differenza spaziale, nella nostra direzione, è data da:

Δd_R = cΔt - v cos(α) Δt

Definendo la solita variabile β = v/c (la conosciamo bene…), i due impulsi luminosi, quello emesso in S₁ e quello emesso in S₂, viaggiano verso di noi, a una distanza costante, l’uno dall’altro, uguale a:

Δd_R = c (1- β cos(α)) Δt

e giungono distanziati da un tempo, decisamente più corto di quello realmente passato dall’emissione da parte di S1 e di S2:

Δt' = Δd_R/c = (1- β cos(α)) Δt .

Lo spostamento compiuto dal nodo in direzione ortogonale alla linea di vista, ovvero lo spostamento sulla sfera celeste, che è quello effettivamente misurato nel passaggio da S₁ a S_2, è dato da:

Δd_T = v sin(α) Δt .

Ne segue che la velocità del getto misurata da terra in questa direzione è pari a:

v' = Δd_T /Δt' ,

ovvero

v' = c (β sen (α))/(1- β cos(α)).

Se il getto si muovesse proprio lungo una direzione ortogonale alla linea di vista (caso fortunato della trattazione qualitativa), si avrebbe:

α = π/2

sin(α) = 1

cos(α) = 0

e, quindi:

v' = v.

La velocità osservata sarebbe effettivamente quella con cui si sposta il nodo. Per un getto diretto verso l’osservatore la velocità apparente può, invece, superare nettamente quella della luce.

Volendo, si possono determinare i valori di v’ per vari valori di β e per vari valori di α. Un esercizio niente male… che dimostra che si ottengono velocità apparenti maggiori di quella della luce solo per valori di β molto prossimi a 1 e per angoli α minori di 90°.

Il film di Hubble

Quando si viaggia a circa il 98% della velocità della luce, tutto può capitare, quasi come essere su un raccordo anulare, in una coda continua, che scorre tutta assieme a oltre 120 km/h. Mi ricordo qualcosa del genere durante un attraversamento di Las Vegas all’ora di punta. 5 o 6 corsie zeppe di macchine lanciate a velocità sostenutissime, una attaccata all’altra. Un’esperienza terribile, con il Sole ovviamente di fronte e anche basso e i continui cambi di corsia per raggiungere le uscite. Il non aver subito o causato un tamponamento è stato un vero miracolo…

Qualcosa del genere capita in un vero e proprio autostrada cosmico: il getto dei buchi neri super massicci galattici. Le particelle di materia vengono accelerate fino a rasentare la velocità della luce e i tamponamenti a catena sono all’ordine del giorno. Questo concitato autostrada è stato osservato e filmato per circa vent’anni da Hubble e appartiene a una galassia che dista 260 milioni di anni luce da noi.

L’impressione è, spesso, ancora più accentuata vedendola da lontano secondo una certa prospettiva: le particelle che compongono i getti appaiono correre a velocità nettamente superiori a quella della luce. In altre parole, accade proprio quello che abbiamo appena descritto. Il getto punta verso di noi sottendendo un angolo molto stretto con la linea di vista. Al suo interno si creano ammassi di materia simili a nodi. Questi nodi emettono luce e in pochi casi sono osservabili nel visibile.

Seguendoli lungo il loro percorso all’interno dell’autostrada si può calcolarne la velocità, come distanza divisa per il tempo e ne nasce l’effetto superluminale. Ciò che si vede nel film di Hubble è lo scontro tra nodi che assomigliano proprio a tamponamenti colossali. Il che implica accelerazioni all’interno del getto.

Sono, infatti, vent’anni che Hubble, a partire dal 1992, riprende di tanto in tanto la galassia ellittica NGC 3862, il cui getto è uno dei pochi  osservabile anche nel visibile. Esso assomiglia a una catena di “perle” , dove le perle sono proprio i nodi di materia. La novità messa in luce dal film è che un nodo  che sembra viaggiare a circa sette volte la velocità della luce raggiunge  e si unisce con uno che lo precedeva a velocità ridotta, ma pur sempre superluminale. Lo scontro esalta ancora di più la luminosità dei “nodi”.

A parte lo spettacolo veramente emozionante, rimane l’estremo interesse fisico dovuto alla possibilità di studiare come l’energia cinetica delle collisioni tra particelle ultraveloci si dissipi in radiazione. Una specie di esperimento di laboratorio su scala immensa e … naturale. Il film non è certo finito e continuerà a mostrare nuovi “nodi” lanciati verso lo spazio, accelerati fino a raggiungere quelli lanciati precedentemente.

Dobbiamo notare che questo tipo di struttura è abbastanza comune nei getti galattici, ma anche nelle stelle in formazione. Come abbiamo detto spesso, l’origine del getto è probabilmente dovuto al materiale che cade verso la massa centrale e che, complice il campo magnetico, viene espulso lungo un “canale” polare molto stretto (l’autostrada…). Se il materiale non cade e non viene rilanciato in modo omogeneo, esso causa delle vere e proprie “bolle”, i nodi, che appaiono come gruppi di automobili che corrono tutte assieme verso un probabile scontro con gruppi più lenti.

La differenza di velocità può essere causata da una maggiore o minore resistenza del mezzo interstellare che viene attraversato dal getto e dai suoi nodi. L’eccezionalità del film è di poter vedere il getto e le sue corse disperate in luce visibile e a una tale grande distanza.

Per aggiungere interesse a interesse, dobbiamo, infatti, notare che il getto che dà luogo a velocità superluminali è misurato a una distanza di centinaia di migliaia di anni luce dal buco nero centrale, una distanza pari a quella dell’intera struttura galattica. Riuscire a mantenere una tale velocità anche a distanze così grandi significa che, per male che vada, le particelle stanno ancora viaggiando a velocità “effettive” molto prossime a quella della luce. L’energia in gioco è veramente spaventosa.

Fenomeni del genere ci fanno capire come i nostri esperimenti negli acceleratori di particelle siano poco più che giochi da bambini per gli attori dell’Universo. Noi non possiamo fare di meglio, ed è giù moltissimo, ma il Cosmo ci costringe a fare un bagno di sana umiltà, che non dovremmo mai dimenticare quando ci si autoincensa con l’attuale, spaventosa, tecnologia raggiunta.

Articolo originale QUI