Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

 

Vi sono moltissimi modi per presentare, descrivere e risolvere il paradosso dei gemelli. Impostiamolo per quello che è, utilizzando un approccio oltremodo intuitivo. Vi prego di non cercare di trarre affrettate conclusioni (sicuramente giuste) ma che sarebbe meglio “toccare” al momento giusto e con la comprensione completa del diagramma di Minkowski.

Stabiliamo, per gradi, in cosa consiste veramente il paradosso. Abbiamo visto che il tempo per chi viaggia a grande velocità appare scorrere più lentamente per un osservatore che sta fermo (o, meglio, che si considera fermo). Come al solito, immaginiamo che il viaggiatore sia un astronauta e chi sta sulla Terra il suo gemello sedentario. Al momento di partire per le stelle essi devono perciò avere la stessa età. Durante il volo, eseguito a velocità costante (sistema inerziale), il tempo del viaggiatore sembra, perciò, scorrere al rallentatore rispetto a quello che viene misurato nel sistema terrestre.

Questo fatto non può certo meravigliarci dato che deriva direttamente dalla trasformazione di Lorentz e, di conseguenza, dalla relatività della simultaneità.  Già a questo punto nasce un problema che non si evidenzia mai abbastanza bene, nelle varie trattazioni che si trovano un po’ ovunque. Quali sono veramente i due sistemi di riferimento? Si parla sempre di “chi sta sulla Terra” e di “chi viaggia sull’astronave”, ma è bene definirli un po’ meglio. Ci aiuta la Fig. 1.

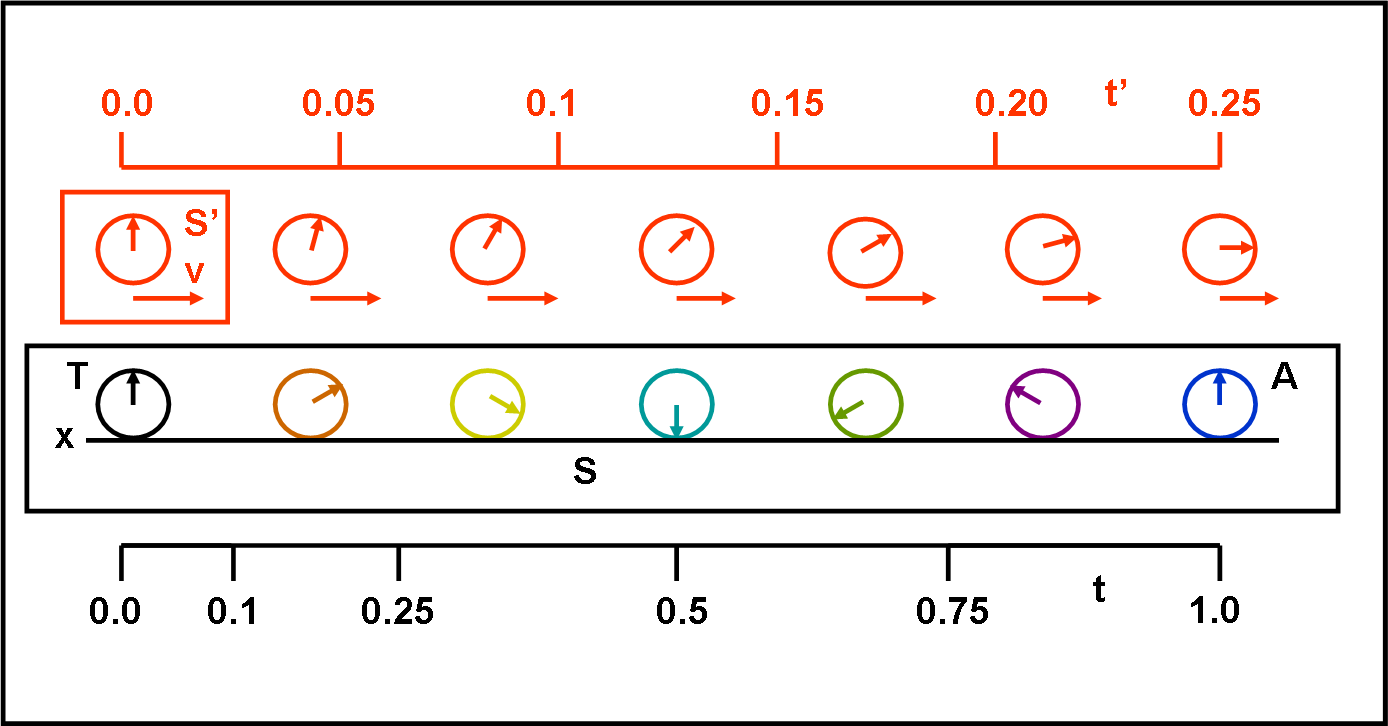
Mentre il viaggiatore (in rosso) rappresenta da solo il sistema di riferimento in moto S’ (non abbiamo bisogno di alti personaggi solidali con lui), l’osservatore a Terra nel sistema S (in nero) ha bisogno di mettere al lavoro molti altri amici che riescano a osservare ciò che capita al viaggiatore. Non facciamo, perciò, lo sbaglio di dire che è sempre lo stesso osservatore che vede il viaggiatore. Ciò è impossibile, dato che la luce impiegherebbe un certo tempo per giungere fino a lui, complicando tutta la faccenda (ne faremmo uso, in seguito, ma al momento evitiamo una possibile ulteriore confusione).

Interviene alla grande la definizione di sistema di riferimento. Esso è composto da infiniti osservatori, che si trovano in posizioni diverse, ciascuno con il proprio orologio e distanziati attraverso un regolo unitario. Una struttura che si muove o che sta ferma (anche se “star fermo” non ha un senso fisico) in modo solidale. Un sistema di riferimento va costruito molto bene, come avevamo fatto all’inizio della descrizione della RR. Sono questi infiniti osservatori che possono verificare ciò che capita al viaggiatore che si muove con velocità v e non certo solo il gemello sedentario. Questo fatto non va mai dimenticato.

Detto in parole che ormai conoscete molto bene, la vera differenza sta nel fatto che il viaggiatore (il sistema di riferimento in moto) utilizza un solo orologio, il suo, mentre nel sistema fermo si è costretti a utilizzare molti orologi, ognuno coincidente con la posizione raggiunta dal viaggiatore.

La Fig. 1 cerca di illustrare molto bene questa situazione. Il sistema S’ si muove rispetto al sistema S e durante il suo movimento basta un unico orologio per scandire il tempo. In S, invece, devono essere utilizzati orologi diversi per effettuare il confronto. Si capisce molto bene, quindi, che ricadiamo nuovamente nel problema della simultaneità che è relativa al sistema che si considera. E da questo fatto si arriva facilmente, attraverso la trasformazione di Lorentz, a un tempo che appare scorrere più lentamente per l’orologio in movimento rispetto a quello segnato dagli orologi degli osservatori fermi.

Nella Fig. 1 abbiamo inserito anche i due assi del tempo relativi ai due sistemi. Rispetto al tempo corrispondente agli orologi dell’asse nero, che compiono un giro completo (loro sono comunque sincronizzati), l’orologio rosso compie solo un quarto di giro. Questo è quello che conferma l’orologio posto in A quando vede passare il viaggiatore spaziale S’ con il suo orologio. Dato che l’orologio della Terra T è sincronizzato con quello di A si dice, solitamente, che il gemello fermo in T vede scorrere più lentamente il tempo del gemello sull’astronave. Il discorso è sicuramente valido, ma si rischia di perdere per strada il concetto di simultaneità che deriva dall’uso di uno o di più orologi.

Anche se tutti gli orologi del sistema fisso sono stati sincronizzati, sappiamo ormai molto bene che essi appaiono NON sincronizzati quando si assiste a un fenomeno che avviene su un sistema in movimento. Da ciò segue la relatività della simultaneità e la dilatazione del tempo. Ripeto, nessuno sbaglia e gli orologi sono veramente sincronizzati nel sistema terrestre, ma essi appaiono sfasati rispetto a quello del viaggiatore.

Scusate le continue ripetizioni, ma proprio in questo concetto sta il nocciolo vero di tutta la RR.

Finché tutto prosegue in questo modo, il rallentamento apparente continua e la dilatazione del tempo non smette assolutamente. Tuttavia, basterebbe cambiare il sistema di riferimento dell’osservatore per ottenere lo stesso identico risultato. Non per niente la trasformazione di Lorentz è perfettamente simmetrica. Se, infatti, fosse il viaggiatore a considerarsi fermo, egli sarebbe costretto ad ammettere che è l’orologio terrestre a girare più lentamente. Questa volta, infatti, l’orologio della Terra (quello del gemello sedentario) è più che sufficiente a descrivere il tempo del suo sistema che si muove solidalmente mentre scorre davanti all’astronave. Il gemello dello spazio, invece, è costretto a utilizzare orologi solidali con il suo sistema, posti teoricamente lungo lo spazio percorso dall’unico orologio del gemello terrestre. E’ adesso lui  che si muove rispetto all’astronauta ed è il suo orologio che sembra rallentare.

Il paradosso non è certo questo! La relatività speciale ci ha insegnato che la simultaneità e tutte le sue conseguenze sono relative al sistema di riferimento usato per descriverle. Nessuno commette un errore, ma vede solo in modo diverso. I muoni ci hanno insegnato che questa situazione, a prima vista assurda, non lo è per niente, dato che per entrambi i sistemi si ottiene lo stesso processo fisico, in accordo con la relatività. Per uno si dilata il tempo, per l’altro si contare la lunghezza e tutto, alla fine, torna perfettamente: il fenomeno fisico rimane inalterato.

Tuttavia, ricordiamolo ancora, se si vive in un sistema di riferimento le conseguenze della RR sono reali a tutti gli effetti. Se niente cambia il movimento relativo, il “mondo” del viaggiatore spaziale e “quello” dell’osservatore stabile sulla Terra rimangono inalterati. Ognuno vive la sua realtà e può anche misurarla facilmente.

Per avvicinarci ancora di più al paradosso dei gemelli, riprendiamo la Fig. 1 e trasformiamola nella Fig. 2. Sono solo cambiati gli orologi! Invece di usare quelli “meccanici” o “atomici” vogliamo usare un orologio biologico: la crescita della barba. Essa si allunga di una certa quantità in funzione del tempo. Se il tempo rallenta deve rallentare anche la sua crescita. Abbiamo preso la barba, ma potevamo prendere il battito del cuore o qualsiasi altra funzione fondamentale del nostro corpo. Se ammettiamo che il cuore ha a disposizione un certo numero N di battiti prima di farci addormentare per sempre, è ovvio che se rallenta il numero di battiti aumenta il tempo necessario a raggiungere N. Insomma, si invecchia “veramente” di meno. La Fig. 2 è del tutto identica alla Fig. 1, anche se adesso tutti gli amici del gemello sedentario si confrontano con la barba che cresce molto meno della loro e diventano sempre più … tristi. Ancora una volta, il gemello sedentario non può confrontarsi direttamente con il gemello in volo. Lo può fare solo attraverso la barba dei suoi amici che deve crescere esattamente come la sua (le barbe sono state… sincronizzate).

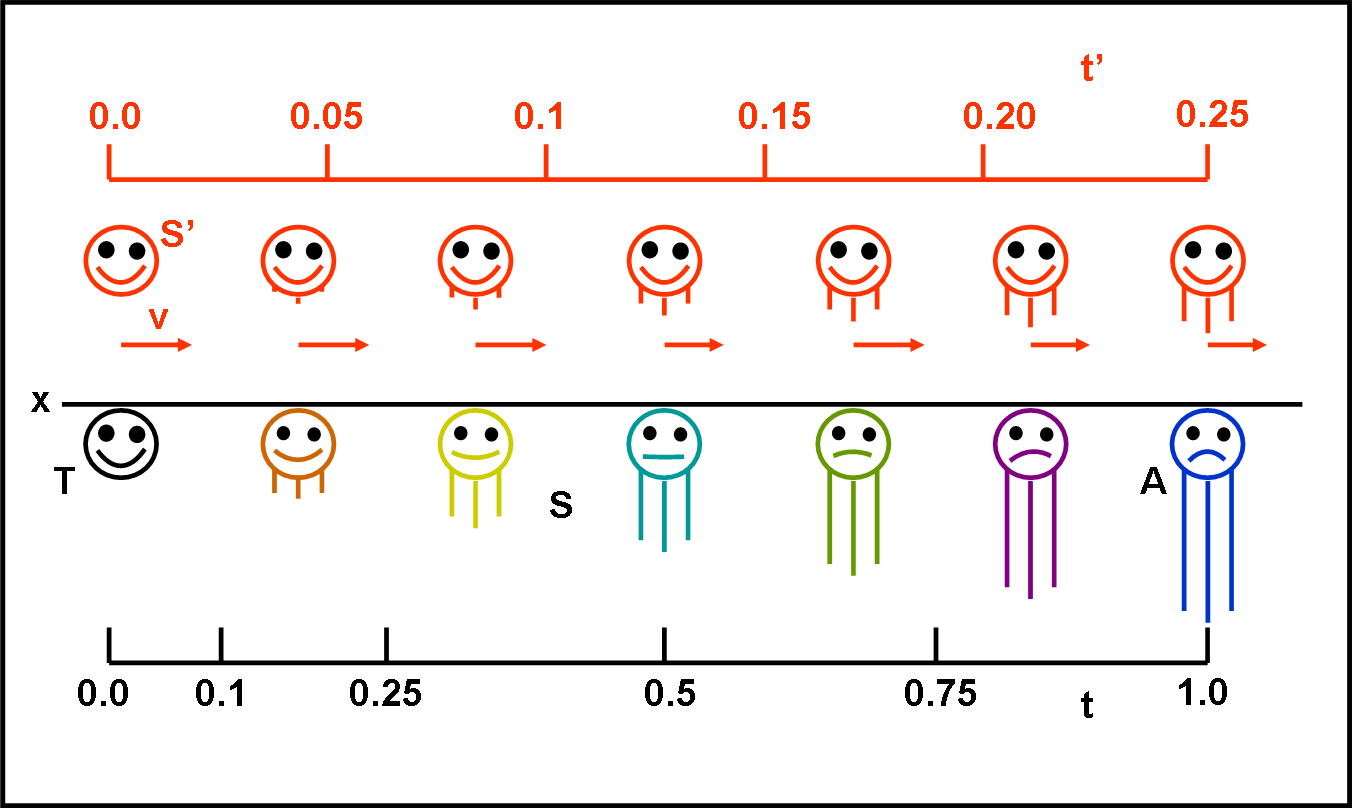
E’ inutile dire che se invertissimo i sistemi di riferimento sarebbe il gemello astronauta a vedere la sua barba crescere sempre di più.

Riflettendo su questi concetti e sulla loro origine non ci si deve sbalordire più di tanto dell’invecchiamento relativo, che è del tutto simile alla dilatazione dei tempi relativa.

Insomma, alla fine si conclude che non c’è niente di male e niente di sconvolgente se sia il viaggiatore che l’osservatore terrestre “vedano” la stessa cosa, ossia un loro invecchiamento precoce rispetto a chi si muove.

Queste considerazioni, che derivano direttamente dalla relatività della simultaneità (e non da un effettivo errore di sincronizzazione degli orologi) ci fanno capire che non esiste nessun paradosso. Tutto è perfettamente spiegabile con la RR. In modo del tutto simile alla favola del muone.

Il vero paradosso nasce quando il viaggiatore vuole confrontare il proprio orologio proprio con quello del fratello gemello sulla Terra e non con uno dei tanti amici di quest’ultimo. Uno potrebbe dire che avendo continuato a viaggiare alla stessa velocità, anche se ha invertito la direzione, dovrebbe rimanere sempre più giovane di chi è rimasto sulla Terra. Ma alla stessa conclusione si giunge invertendo gli attori. Per il viaggiatore dovrebbe invecchiare di meno il gemello terrestre.

Fin qui non ci sarebbe nessun paradosso, anche se non vi sarebbe una vera soluzione. Quando s’incontrano cosa succede veramente? Tornano alla stessa età? O cos’altro? Dato che nella RR tutto è perfettamente simmetrico, uno si potrebbe aspettare che quando il viaggiatore torna al punto di partenza le differenze di tempo apparente si annullino in qualche modo.

E’ proprio a questo punto che nasce il paradosso, dato che quando i due gemelli s’incontrano è proprio il viaggiatore a essere invecchiato di meno. Si è rotta la simmetria della RR? No, nemmeno per sogno, il vero motivo è che si è rotta l’inerzialità dei sistemi di riferimento. Quello della Terra non ha mutato la sua velocità (o il suo star fermo, che è la stessa cosa), mentre l’astronauta ha dovuto cambiar direzione. Sappiamo molto bene che anche solo cambiare direzione vuol dire introdurre un’accelerazione e tutta la RR cade! La spiegazione sembra ovvia, anche se è un po’ come passare la castagna bollente al vicino… La RR non può risolverlo e può pensarci la relatività generale che tratta proprio con le accelerazioni e che accetta la mancanza di simmetria.

Non pensiamo che sia un discorso veramente concluso. Ancora oggi si sta discutendo sulla necessità di passare realmente alla relatività generale per superarlo. Sicuramente è più facile. Noi, però, dobbiamo ancora completare l’analisi della RR e non vogliamo addentrarci nelle curvature dello spaziotempo (ogni cosa a suo … tempo). L’esercizio che cercheremo di fare è allora risolvere il paradosso con la sola RR, tenendo, però, in conto che il sistema in movimento, pur rimanendo inerziale, ha cambiato direzione. Assumeremo, però, che è mutata la direzione, ma non il modulo della velocità. Un’esperienza praticamente impossibile senza una qualche forza che agisca sull’astronave, ma che si può ottenere, considerando trascurabili i pochi istanti necessari alla decelerazione e all’accelerazione.

In altre parole, possiamo ricostruire perfettamente il viaggio di andata e ritorno solo attraverso la RR. La vera novità di questo approccio, che utilizza il diagramma di Minkowski a piene mani, è quello di dimostrare che anche con la sola RR il risultato non è simmetrico: il viaggiatore invecchia di meno e questo viene confermato sia dal sistema che viaggia sia dal sistema che è fermo!

Qualcuno potrebbe dirmi: “Non è assolutamente una novità. Tu stesso hai dimostrato in altri articoli che il cambiamento di direzione comporta un’esauriente spiegazione della mancanza di simmetria finale”. Sì, avrebbe ragione… ma la vera novità è che questa volta troveremo la medesima conclusione sia mettendoci nel sistema terrestre sia in quello del viaggiatore. L’importante è che i due gemelli mantengano sempre un contatto “visivo” e facciano un po’ di conti.

E’ inutile continuare, dato che, per andare avanti, Minkowski non deve avere più segreti e deve anche essere introdotta la composizione relativistica delle velocità.

Per adesso c’è abbastanza materia su cui riflettere. Impostare bene un esercizio è già una buona parte della soluzione.

Ciò che abbiamo descritto con tante parole e figure apparentemente banali rinsalda le basi della relatività della simultaneità, della dilatazione dei tempi e della diversa scala temporale che ogni sistema deve adottare. Non consideriamolo come una semplice ripetizione…

 

QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli