Facciamo un passetto indietro per richiamare lo spazio a noi più comune, quello euclideo.

Immaginiamo che ci venga regalata una bella asta rigida di una certa lunghezza. Purtroppo, noi non abbiamo a disposizione nessun “metro” per misurarla. Abbiamo solo un disegno perfettamente in scala 1:1 di una circonferenza avente raggio unitario. Non ci resta che far coincidere un estremo dell’asta con il centro della circonferenza e guardare dove va a finire l’altro estremo. Se esso esce dalla circonferenza possiamo dire che la nostra asta è maggiore dell’unità di misura; se rimane all’interno della circonferenza vale il contrario.

Volendo, potremmo anche vedere di quanto l’asta è maggiore o minore del raggio unitario della circonferenza e stabilire in un modo un po’ rozzo la sua lunghezza effettiva. Avendo a disposizione un sistema cartesiano accurato, potremmo ottenere molto di più. In ogni modo il confronto con il raggio della circonferenza ci basta per avere una prima stima della lunghezza della nostra asta, se non altro se è maggiore o minore dell’unità. Quanto detto è raffigurato con estrema semplicità in Fig. 1.

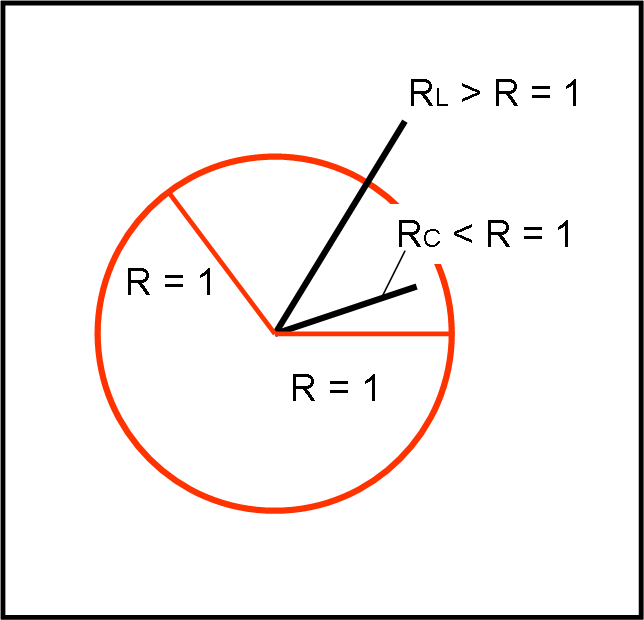
Molti di voi si saranno messi a ridere… Abbiamo usato un procedimento estremamente semplificato e rudimentale. Si poteva certamente fare di meglio. Tuttavia, teniamo ben presente il procedimento usato, dato che con le opportune modifiche lo useremo nel diagramma di Minkowski per ottenere immediatamente (o quasi) la visione grafica della dilatazione dei tempi e della contrazione della lunghezza senza aver bisogno di usare formule matematiche.

Cerchiamo di essere un po’ più chiari: le formule, o qualcosa che si colleghi a loro, le abbiamo giù utilizzate (per via matematica e/o grafica) per stabilire come si trasformano gli assi x e t (ho ripreso a usare t invece di T, dato che è solo una questione di unità di misura; basta porre c = 1 e siamo a posto) quando un sistema si muove con una certa velocità v rispetto a uno considerato fermo e per determinare l’unità di misura su tali assi. Stiamo, ovviamente, parlando dell’iperbole di calibrazione, il luogo dei punti che descrivono l’invariante s², ossia una vera e propria “distanza” spaziotemporale. Ricordiamo ancora che questa “distanza” non ha niente a che vedere con la distanza classica del nostro mondo euclideo dove si disegnano i punti, ma ha un significato ben preciso nello spaziotempo, diventato a tutti gli effetti un sistema in cui si misurano gli eventi. Qualcosa di estremamente più realistico e completo.

Questa “distanza” assume lo stesso significato del raggio della circonferenza con la quale abbiamo iniziato l’articolo: essa ci regala il luogo dei punti a distanza costante da una certa origine degli assi. Se qualcosa supera la curva di distanza unitaria vuole dire che la sua “lunghezza” è maggiore dell’unità; se, invece, rimane all’interno della curva di calibrazione la sua “lunghezza” è minore.

Prima di passare alla parte “pratica” cerchiamo di notare ancora una volta come siamo già riusciti a trattare lo spaziotempo alla stregua dello spazio quotidiano. Possiamo parlare di distanze e di lunghezze di segmenti che rappresentano qualcosa di ben più generale, ossia di intervalli spaziotemporali. Il tempo è ormai diventata una coordinata del tutto equivalente a quelle spaziali.

Noi stiamo lavorando con uno spazio a una dimensione (x e/o x’), ma potremmo tranquillamente lavorare con uno spazio a tre dimensioni, ossia definire un punto con le sue tre coordinate cartesiane x, y e z. A queste tre coordinate siamo ora perfettamente in grado di aggiungerne una quarta, il tempo, che si va a mischiare con loro e diventa del tutto simile in uno spaziotempo in cui ogni punto si è trasformato in evento.

Abbiamo in tal modo, anche se velocemente, introdotto il concetto di quadrivettore, la base matematica di tutto lo spaziotempo di Minkowski. Esso permette di descrivere il moto di un corpo qualsiasi nello spaziotempo a quattro dimensioni, in cui ogni evento del corpo è definito dalle quattro coordinate (x,y,z,t). Cerchiamo di capire appieno la grandezza e la generalità di questo approccio che sembra oltremodo banale e quasi ovvio. Siamo riusciti a rappresentare perfettamente lo spaziotempo di Einstein, avendo la possibilità di agire con  quattro coordinate, misurabili con la stessa unità di misura (ad esempio il metro o -se si preferisce- il secondo). Due esempi di questa eccezionale capacità che abbiamo acquisito.

Vi ricordate la solita rappresentazione del palloncino che si gonfia e che è gioia e dolore per chi si avvicina all’evoluzione del Cosmo? Quante volte abbiamo detto: “Stiamo attenti a non confondere l’Universo con l’intero palloncino! L’Universo è solo la superficie sferica (a due dimensioni), mentre il raggio della sfera si riferisce al tempo che scorre. Le traiettorie che attraversano la sfera sono VIETATE, dato che sono del tutto estranee all’Universo fisico.” Adesso, possiamo invece dire che queste traiettorie sono perfettamente definite, dato che rappresentano le linee di Universo, ossia le traiettorie di un evento caratterizzato sia dalle coordinate spaziali che da quella temporale. Il passato, il presente e il futuro possono essere rappresentati con una sola figura, su cui si possono effettuare tutte le misure che si vogliono, tenendo solo presente che questo spaziotempo non è più euclideo, ma segue regole diverse. Imparate queste, niente è veramente precluso!

Usiamo un’altra analogia per comprendere il passo in avanti che è stato fatto. Immaginiamo di congelare il tempo e di fermare il “tutto” in un certo istante (un po’ come la bella Addormentata nel Bosco). Esiste ancora l’Universo? Sicuramente sì.

Stelle, pianeti, galassie, alberi, uomini, atomi, elettroni, quark sono ancora loro e del tutto concreti. Esistono anche gli eventi che però sono fissi, immobili, dei veri punti. La stessa cosa che capita a chi vive in uno spazio a due dimensioni (x,y) e che non può assolutamente “alzarsi” o “abbassarsi” lungo l’asse z. Analogamente, chi vive in uno spaziotempo che conservi le tre coordinate spaziali x, y e z continua a esistere, ma non può “alzarsi”, ossia non può andare avanti o indietro nel tempo (che ha lo stesso identico significato dell’asse z nello spazio a due dimensioni). L’Universo fisico diventa allora l’acquisizione della dimensione in più, del tutto simile all’asse z per gli abitanti di Flatlandia. Né più né meno. Lo spaziotempo di Minkowski permette proprio di descrivere e di lavorare sulle quattro dimensioni in modo del tutto analogo a come siamo capaci di lavorare sulle tre, con un semplice diagramma cartesiano. Un Universo statico, descritto spazialmente nelle tre dimensioni, diventa un Universo dinamico in evoluzione nelle quattro dimensioni. Stiamo solo attenti a non pretendere troppo da questa coordinata in più. Essa viene utilizzata e legata alle altre con estrema facilità, ma rimane comunque un qualcosa di speciale se la vediamo in modo diverso. Ad esempio come freccia evolutiva legata all’entropia e via dicendo. Il tempo rimane sempre qualcosa di misterioso anche se trattabile matematicamente e graficamente.

Torniamo, allora, “a bomba” e dedichiamoci a rappresentare, in modo grafico, quanto dimostrato dalla RR con l’ausilio della trasformazione di Lorentz. Abbiamo bisogno di saper disegnare solo due cose: gli assi t’ e x’ trasformati (e lo sappiamo fare anche graficamente senza alcun problema) e le curve di calibrazione che , in fondo, sono due semplicissime iperboli equilatere, curve alla portata di tutti. Ovviamente, per fare questo dobbiamo conoscere il valore della velocità v del sistema in movimento, ma assolutamente niente di più! Disegniamo, allora, in Fig. 2 quanto appena detto: un sistema di riferimento S’ che si muove con velocità v rispetto a S e le due curve di calibrazione che ci dicono immediatamente come “viaggia” l’unità di misura al variare della velocità. Una figura che abbiamo giù usato nella terza parte.

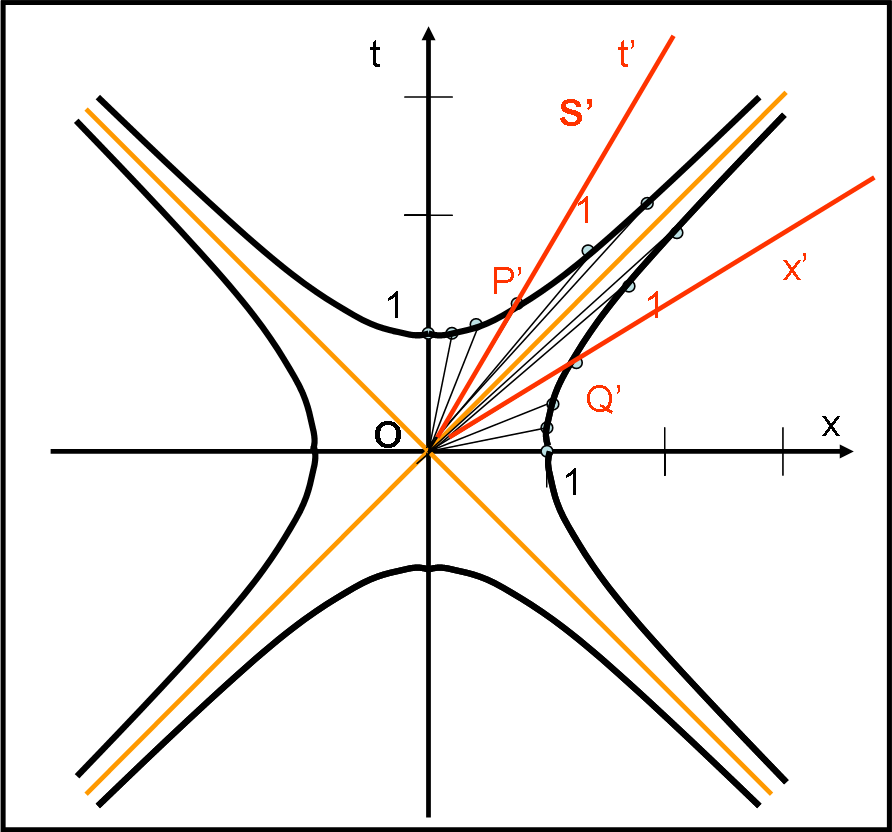
Per determinare con facilità le conseguenze della RR bisogna ricordarsi perfettamente i concetti di simultaneità relativa, quelli su cui abbiamo “battuto duro” fino all’esaurimento. Per il sistema S la linea di simultaneità è l’asse x e tutte le sue parallele; per il sistema S’ è l’asse x’ e tutte le sue parallele. Ricordiamoci, inoltre, che la vera differenza tra ciò che vede un osservatore “fermo” e ciò che vede chi è solidale con il sistema in movimento è legata sempre e comunque al numero di orologi che si stanno usando per eseguire le misure. Cerchiamo, quindi di farli intervenire per aiutarci nella descrizione della nostra piccola impresa grafica. Immaginiamola come una piccola avventura che poi “trascriveremo” in modo più serio.

Cominciamo con la dilatazione dei tempi, che è la più immediata e intuitiva. La RR ci dice che l’orologio di chi si muove è visto rallentare se visto da un osservatore fermo. Nel primo caso S è fermo e S’ è in moto. Se ne deduce, come ormai dovremmo sapere molto bene, che se siamo solidali con S’ basta un solo orologio per scandire il tempo, mentre nel sistema S ce ne vogliono molti. Guardiamo la parte bassa della Fig. 3 , quella contenuta dentro il riquadro. L’orologio rosso è solidale con S’ e si muove verso destra. Mentre effettua il percorso da A a B lui segna tranquillamente il tempo che passa. Nel sistema S,invece, vi è bisogno di usare l’orologio azzurro quando l’orologio di S’ è in A e l’orologio verde quando arriva in B. So che ne abbiamo parlato varie volte, ma è meglio continuare a ripetere quando si ha a che fare con il concetto base della simultaneità.

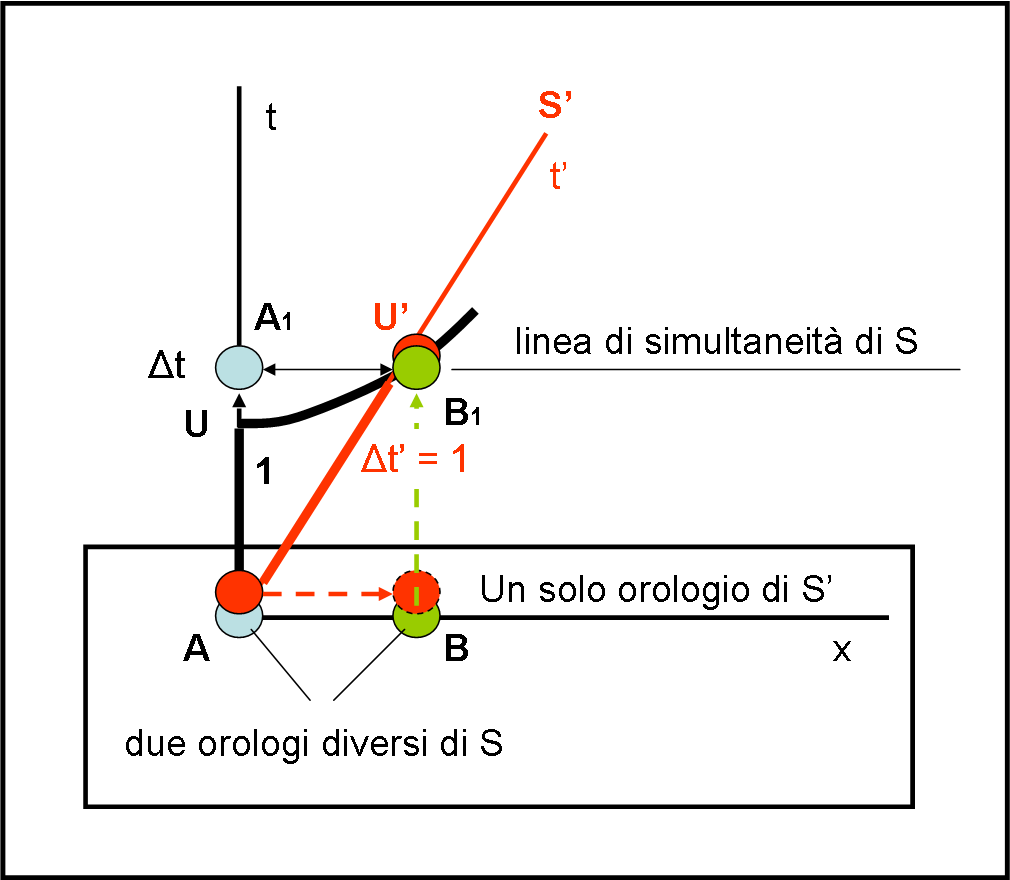
Finora abbiamo lavorato solo nello spazio e il tempo è stato misurato dagli orologi. E’ venuto il momento di introdurre l’asse del tempo. L’orologio azzurro, mentre l’orologio rosso si è spostato verso destra, si è mosso lungo l’asse del tempo in verticale e si porta in A₁. Lui è infatti “spazialmente” fermo nel sistema S che è rappresentato dai due assi cartesiani t e x. Cosa fa, invece, l’orologio rosso? Si muove sia spazialmente che temporalmente seguendo la legge della RR e quindi descrive il suo asse del tempo che è la linea rossa. Perché questa linea è il suo asse del tempo? Perché rispetto a questa linea lui rimane FERMO, essendo solidale con S’. Il sistema S lo vede andare verso destra, cambiando “spazio”, ma lui si sente perfettamente fermo lungo l’asse rosso.

In altre parole, l’orologio rosso gira tranquillamente segnando il suo tempo mentre il sistema S lo vede spostare sia in x che in t.  L’orologio verde entra in azione quando l’orologio rosso segna una certa ora misurata con il suo tempo. L’orologio verde lo segue come un’ombra nello spaziotempo, muovendosi verso l’alto lungo una parallela all’asse t (lui è fermo nel sistema S) e si porta in B₁. A un certo momento decidiamo di controllare il tempo Δt’ (misurato perfettamente dall’orologio rosso lungo la linea rossa) e chiediamo all’orologio verde di “mettersi d’accordo” con quello azzurro per dirci quanto tempo è passato, nel loro sistema S.

Loro sanno perfettamente di essere sincronizzati, per cui devono segnare lo stesso tempo. Qual è la linea di simultaneità per loro? Quella parallela all’asse delle x. Per sapere il tempo passato Δt basta allora che si guardi l’ora segnata dall’orologio azzurro quando è “in linea” con l’orologio verde.

Ah, come sarebbe bello applicare il teorema di Pitagora al triangolo ABB₁ o AA₁B₁! E’, invece non possiamo farlo, dato che la geometria di Minkowski non è euclidea… E’ necessario introdurre la curva di calibrazione, quella che ci dice quanto vale l’unità di tempo su S e quanto vale su S’. Consideriamo, ad esempio, che Δt’ (AU’) sia proprio uguale all’unità di tempo su S’. E’ facile allora tracciare la curva di calibrazione fino a che incontri l’asse x, ossia segni l’unità di tempo nel sistema S. Disegniamo la curva nera sapendo che la ”distanza” spaziotemporale AU = AU’ = 1 deve rimanere costante (invariante relativistico). Non ci resta che guardare l’ora segnata dall’orologio azzurro sincronizzato con quello verde. Come detto già prima, questa è quella segnata dall’orologio azzurro in A₁.

Risulta immediato che la “distanza” AA₁ è DECISAMENTE più grande dell’unità di S (AU). In poche parole ciò che per l’orologio rosso di S’ è 1, per S è decisamente qualcosa di maggiore di 1. Se ne conclude che per S il tempo di S’ scorre più lentamente. Infatti, mentre per il “rosso” è passato solo 1, per il “nero” è passato un tempo maggiore di 1. Abbiamo utilizzato lo stesso procedimento dell’inizio dell’articolo, con l’iperbole al posto della circonferenza.

Perché è successo tutto ciò? Solo e soltanto perché la simultaneità degli orologi di S è relativa al loro sistema. Per S’ non c’è stato bisogno di utilizzare la simultaneità, avendo usato un solo orologio, ma per S invece sì, avendo dovuto utilizzare due orologi posti in luoghi diversi. Pensateci bene, perché il succo di tutta la RR sta in questo concetto fondamentale.

Scusate se ho usato un sacco di parole e se ho quasi reso la misura del tempo misurato dall’orologio in moto, effettuata nel sistema fermo, una specie di avventura o di favola. Come tutte le favole ha reso “concreti” dei processi geometrici e matematici. Non prendete ciò che ho detto come “realtà” assoluta, ma solo come un metodo per rendere più “tattile” l’operazione da svolgere che è ben più semplice e immediata.

La Riportiamo in Fig. 4. Disegniamo l’asse t’ di S’ e la curva di calibrazione. Consideriamo l’intervallo Δt’ = 1 (ma potevamo prendere qualsiasi valore) che termina sulla curva di calibrazione unitaria. Tracciamo la perpendicolare all’asse t (questa perpendicolare è l’asse di simultaneità per S) e troviamo il tempo t che definisce il tempo passato su t’ se osservato da S, ossia Δt.

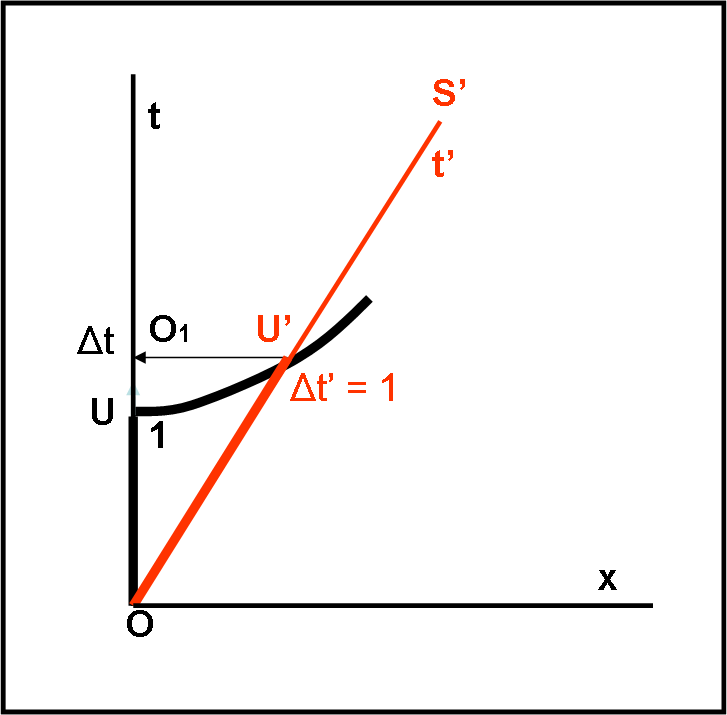
Si vede immediatamente che Δt è maggiore dell’unità del tempo di S (sta sopra alla curva di calibrazione). Δt, misurato in S e relativo a Δt’, è decisamente più lungo dell’unità. Il tempo t’ scorre più lentamente se visto da S! La dilatazione dei tempi viene disegnata con una semplice proiezione…

Utilizzando la stessa identica figura possiamo dimostrare facilmente che il fenomeno della dilatazione dei tempi è perfettamente simmetrico (Fig. 5). Non raccontiamo nuovamente la favola dei due orologi: ci basta ragionare sul grafico. Immaginiamo di trasferirci su S’ e di voler misurare il tempo passato su S. E’ ovvio, adesso, che è S che si muove rispetto a S’ e che i due orologi sono quelli di S’ e … via dicendo.

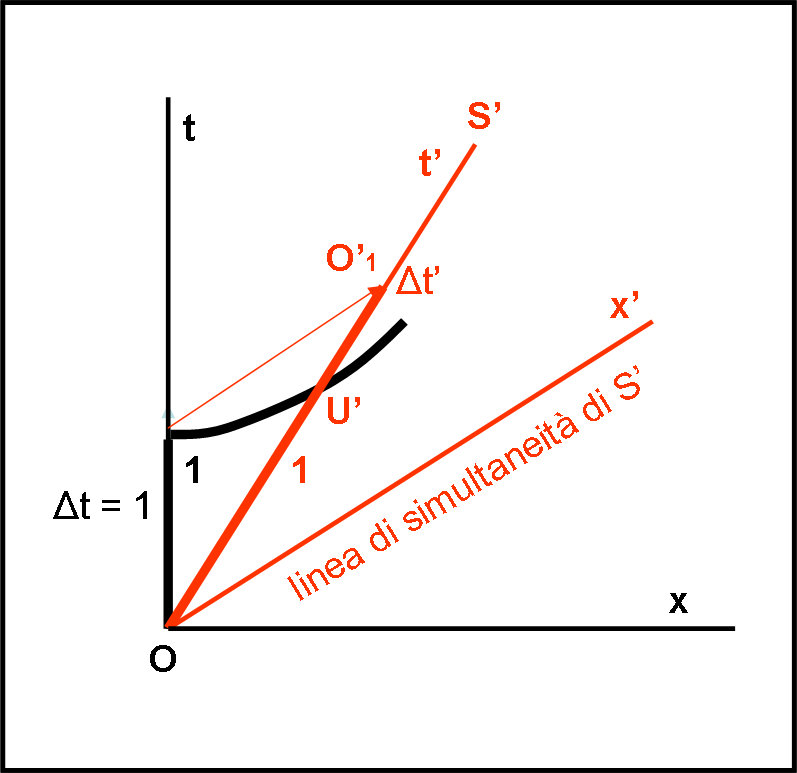
Cosa dobbiamo fare? Semplice. Consideriamo come intervallo di tempo da misurare su S’ quello unitario su S, ossia Δt = 1. Quale sarà quello corrispondente su S’? Basta tracciare la linea di simultaneità per S’ (la stessa identica cosa che avevamo fatto per S) fino a incontrare t’. OO₁’ indica come il sistema S’ vede l’unità di tempo Δt = 1 di S. E’ immediato notare che OO₁’ è decisamente più “lungo” dell’unità di tempo OU’ di S’ e quindi per S’ è l’orologio di S che gira più lentamente. La simmetria è perfettamente rispettata.

Bene, vi consiglio di tornare a rileggere la parte romanzata precedente ed essa apparirà, adesso, decisamente più semplice e comprensibile. Vi lascio il tempo di digerire tranquillamente questo “gioco” puramente geometrico, che ha bisogno di formule solo e soltanto per disegnare la curva di calibrazione (che è sempre la stessa) e per calcolare la pendenza di t’ e x’. Dato che l’unica variabile è v/c, potete divertirvi a vedere come aumenta la dilatazione dei tempi aumentando la velocità… Potete anche scrivere delle tabelle… (ehm...ehm...). Vedrete, anche, che per v = c il tempo non scorre assolutamente per un sistema in movimento quando è visto da quello che si considera fermo. Ma, ripeto ancora, questo NON vuol dire assolutamente che un oggetto che vada alla velocità della luce non si MUOVA e nemmeno che il suo orologio non giri. Esso appare immobile solo per chi lo guarda da fuori…

La prossima volta costruiremo graficamente la contrazione delle lunghezze. Sembrerebbe banale e immediato, dato che esiste anche la curva di calibrazione relativa all’unità dello spazio. Tuttavia, se si applicasse il procedimento appena usato troveremmo una … dilatazione invece che una contrazione! Ancora una volta, solo una attenta riflessione sulla relatività della simultaneità può sciogliere l’enigma.