Accingiamoci a vedere, direttamente nel diagramma di Minkowski, come un’asta rigida in movimento viene vista contratta nel sistema di riferimento considerato fisso. Ancora una volta è essenziale comprendere bene la differenza tra chi usa due orologi e chi ne usa uno solo (anzi non lo usa per niente!).

Se nel sistema in moto S’ si pone un’asta rigida essa deve giacere nel relativo asse x’, ossia nell’asse dello spazio o se preferite nell’asse di simultaneità (t’ = 0). La misura dell’asta, in questo sistema, è definita perfettamente dall’unità di misura e non ha assolutamente bisogno di un orologio. Ricordatevi come Einstein aveva preparato perfettamente il suo sistema di riferimento attraverso aste rigide e orologi sincronizzati… (vedi l’articolone in evidenza sulla RR).

Il sistema fermo S ha invece bisogno di due orologi (ovviamente sincronizzati tra loro) per misurare l’asta che si muove. In altre parole, S deve misurare le due estremità dell’asta con due orologi diversi. Vediamo “rozzamente” cosa succede in Fig. 1.

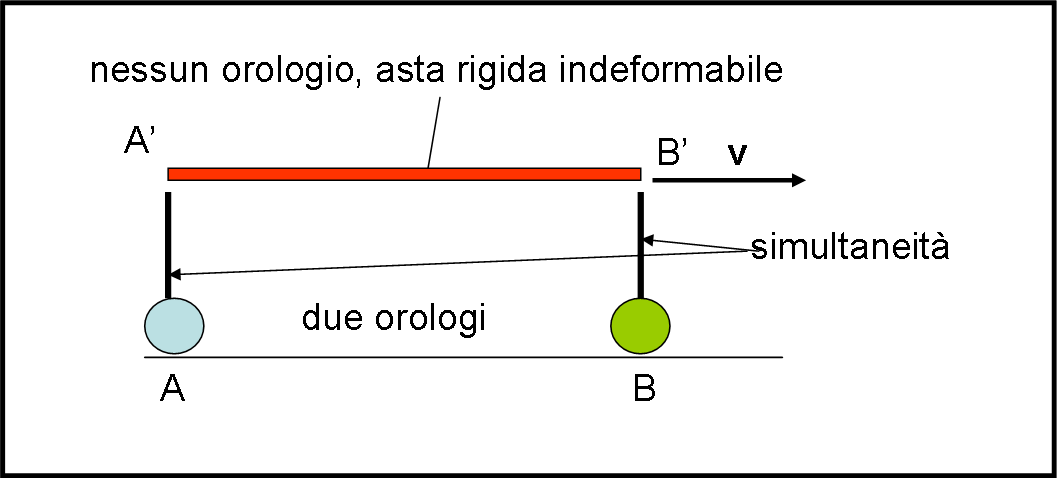
L’asta A’B’ del sistema S’ si muove con velocità v. Per misurare la sua lunghezza da S, dobbiamo misurare il tempo in cui gli orologi  azzurro e verde di S vedono passare i due estremi dell’asta in movimento. Essi, ovviamente, misurano secondo la loro linea di simultaneità che è rappresentata dai due trattini neri verticali. Né più ne meno quanto avevamo fatto per misurare la contrazione delle lunghezze con l’orologio a luce…

Vediamo nella Fig. 2 come questo schema logico, estremamente semplificato, si trasforma nel diagramma di Minkowski. x e t sono gli assi ortogonali di S, mentre x’ e t’ quelli “trasformati” di S’. Consideriamo l’asta rigida A’B’ solidale con S’ di lunghezza L’. Come detto, essa giace sull’asse x’ per definizione. Al passare del tempo, gli estremi dell’asta si muovono lungo due assi paralleli all’asse dei tempi t’, mantenendo costante la lunghezza L’ (è o non è RIGIDA?).

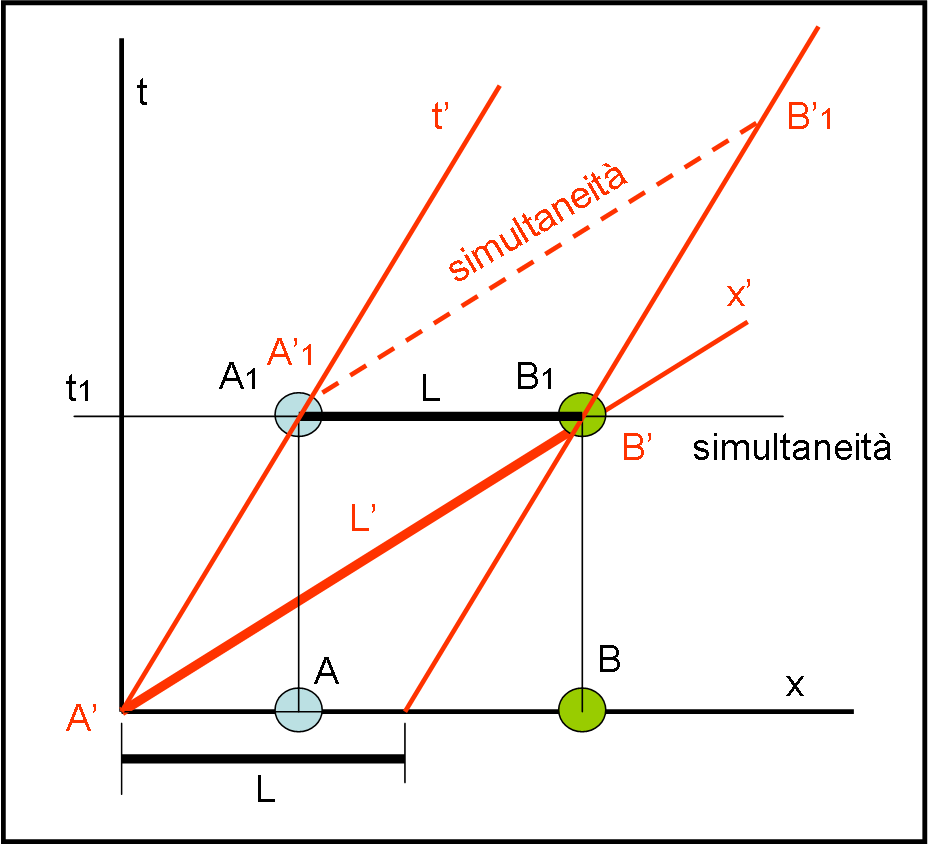
Cosa fanno due orologi A e B di S per potere misurare l’asta… Essi si spostano al passare del tempo lungo linee verticali. Quando l’orologio verde, ad esempio, si trova in B₁ e vede passare  l’estremo B’, decide il tempo della misurazione t₁. Nello stesso istante l’orologio azzurro effettua la sua misura dato che sono sincronizzati e noi abbiamo bisogno che essi misurino i due estremi dell’asta nello stesso istante.

Sappiamo bene, però, che la simultaneità è relativa  e A₁ misura l’estremo A’₁ che non è simultaneo con B’ (ma con B’₁) nel sistema S’. In altre parole, i due orologi di S misurano gli estremi in due tempi diversi del sistema S’. Ne deriva che la lunghezza dell’asta, nel sistema S, appare essere L.

Possiamo concludere subito che l’asta si è contratta se è vista nel sistema S? Sembrerebbe di sì, ma commetteremmo un errore molto grave! Come già detto non possiamo confrontare lunghezze, corrispondenti a sistemi diversi, direttamente nella figura, ma dobbiamo utilizzare le diverse unità di misura, quelle che vengono descritte dalla famosa iperbole di calibrazione. Solo tenendo conto delle unità di misura possiamo dire se è veramente più lunga l’asta solidale con S’ o quella osservata e misurata da S.

Per semplificare il disegno facciamo una piccola considerazione. La lunghezza L tra A₁ e B₁ è esattamente uguale a quella riportata nell’asse x. Eliminiamo quindi gli orologi e le altre linee che ormai hanno fatto il loro lavoro e portiamoci nella Fig. 3, estremamente semplice e perfetta per la decisione finale.

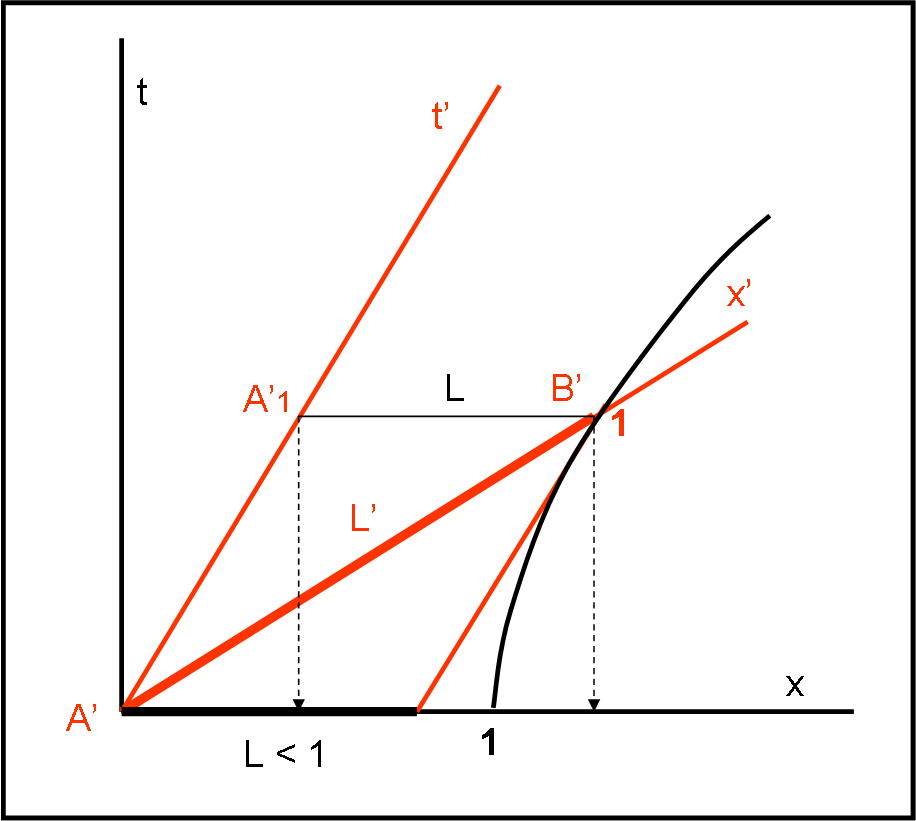
In questa figura abbiamo “solo” aggiunto l’iperbole di calibrazione relativa all’unità di misura dello spazio (ossia delle lunghezze). Poniamo anche, sempre per maggiore semplicità, che la lunghezza L’ dell’asta sia proprio l’unità. Adesso sì che possiamo renderci conto della contrazione delle lunghezze! La lunghezza L viene confrontata, sullo stesso asse di riferimento x di S, con la distanza unitaria di questo asse. Questa è un’operazione ammissibile dato che stiamo lavorando su un unico sistema.

Bene, nessun problema a concludere che L è veramente minore di 1! Possiamo, quindi, confermare graficamente, attraverso il “nostro” diagramma di Minkowski, che una lunghezza L’ (unitaria) di S’ appare contratta nel sistema di riferimento S considerato fermo.

Attenzione a non commettere un errore che viene fatto spesso (perfino Paolo c’era caduto per un attimo…). Per analogia con quanto eseguito nello studio della dilatazione dei tempi, potremmo pensare di proiettare direttamente la lunghezza L’ sull’asse x. troveremmo una lunghezza MAGGIORE dell’unità. Altro che contrazione… avremmo ancora una dilatazione!

L’errore sta nel fatto che prima di proiettare la lunghezza dobbiamo usare la simultaneità del sistema S. I punti da proiettare devono essere, per quanto detto precedentemente, A’₁ e B’. La differenza delle loro proiezioni è ancora una volta L minore dell’unità!

Il punto chiave da comprendere per non meravigliarsi più di tanto è il fatto che anche per la contrazione delle lunghezze la misura dipende solo e soltanto dal tempo misurato da uno (o anche nessuno) oppure da due orologi. Gira e rigira questo è il concetto fondamentale di tutta la RR.

Non ci resta, adesso, che dimostrare la perfetta simmetria della situazione, utilizzando la Fig. 4. Portiamoci sul sistema S’ e vediamo come esso misura un’asta rigida solidale con il sistema S. L’asta unitaria si sposta lungo il tempo t, in modo perfettamente verticale. Come fatto prima, dobbiamo misurare la sua lunghezza attraverso due orologi posti su S’, che hanno come linea di simultaneità l’asse x’.

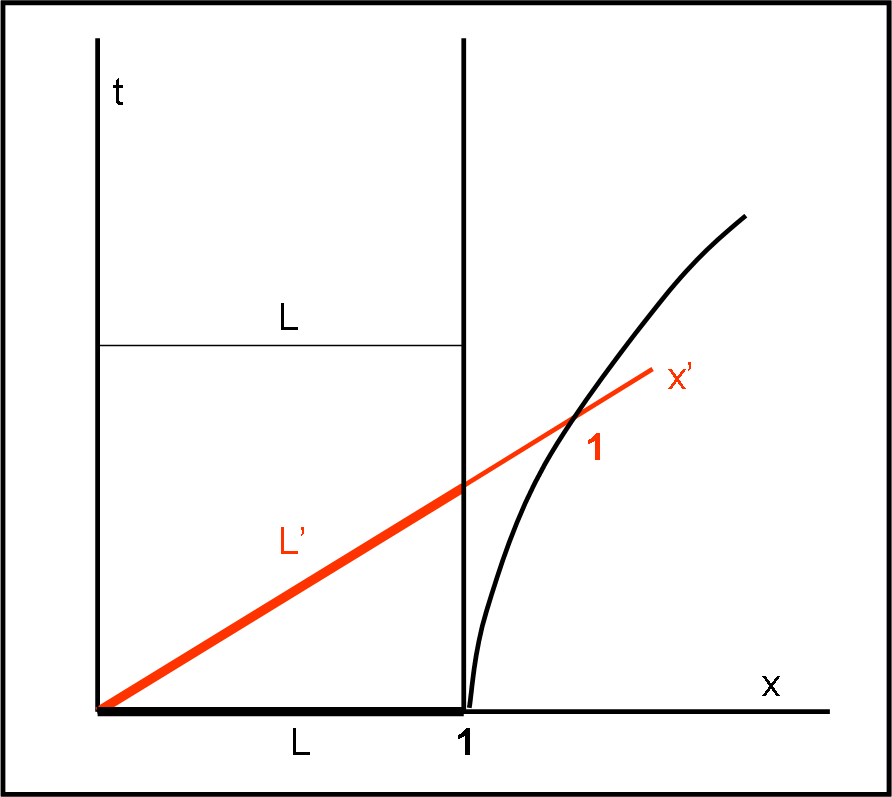
Ne consegue che la lunghezza misurata nel sistema S’ è L’ che giace proprio sull’asse x’ (o su una sua parallela, nel caso più generale). In questo caso ci accorgiamo subito che il nostro occhio abituato, allo spazio euclideo, ci porterebbe a sbagliare completamente! Il segmento L’ ci appare più lungo di L. E, invece, non è assolutamente vero e ce lo dimostra la curva di calibrazione.

L’unità di misura su x’ è nettamente più lunga di L’, mentre L è proprio uguale all’unità. Ancora una volta abbiamo ottenuto una contrazione delle lunghezze!

Ovviamente, tutto ciò che abbiamo trovato per via puramente grafica viene confermato dalle formulette regalateci dalla trasformazione di Lorentz. Paolo, nei suoi commenti, ce l’ha già dimostrato esaurientemente. Comunque è un esercizio che potete fare da soli per capire se avete veramente … capito! In caso contrario, sarebbe meglio andarsi a rileggere i capitoli precedenti…

Potremmo anche fermarci qui e sospendere per un poco la RR, seguendo la linea di azione che ho proposto ieri. Tuttavia, vale la pena aggiungere ancora qualche considerazione…

Senza entrare nei dettagli troppo tecnici (mi spiace per Alvy, ma prima o poi ci arriveremo) che ci porterebbero alla radice quadrata di un numero negativo (ossia, ai numeri complessi e immaginari), vedremo come per via estremamente intuitiva il diagramma di Minkowski permette di rappresentare l’Universo di tutti gli eventi, passati, presenti e futuri, in una sola figura.

Basta saperlo dividere sapientemente attraverso il ben noto cono di luce. Vedremo anche perché il percorso rettilineo è quello più lungo che congiunge due eventi (come già dimostrato dal paradosso dei gemelli) e, infine, risponderemo alla domanda estremamente puntuale di Simone Lotti: “Due eventi possono invertire il loro ordine cronologico se osservati in sistemi diversi?”. La risposta sarà, “ovviamente”, sì.

Alla prossima e poi divertitevi pure con il diagramma di Minkowski. Si possono fare e comprendere infiniti casi particolari. Più in là, dopo aver digerito per bene tutti i vari capitoli, proveremo anche a fare qualche esercizio…

Viva l’ordine (non troppo ordinato, però…).