Categorie: Relatività
Tags: Minkowski quiz relatività ristretta relatività speciale sistemi di riferimento soluzione velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:14
SOLUZIONE del quiz sulla relatività della velocità della luce **
Come detto, descriviamo l’intero esperimento solo per via grafica, applicando ciò che ormai sappiamo sul diagramma di Minkowski, un vero pozzo delle meraviglie!
Iniziamo con noi in viaggio alla velocità di 0.6. Disegniamo qualche linea in più rispetto alla figura inserita nel QUIZ. Linee che ormai sappiamo tracciare senza problemi. Riferiamoci, quindi, alla Fig. 2. Gli assi del nostro sistema in movimento sono, ovviamente, x’ e t’.
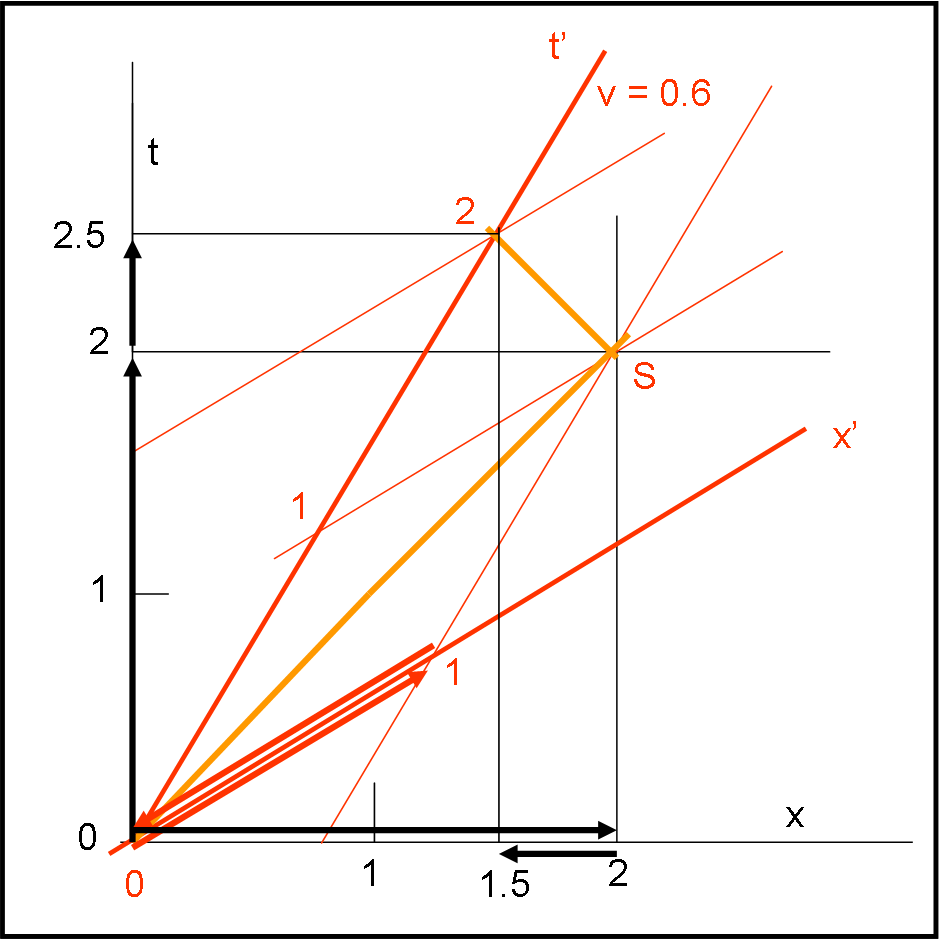
In O accendiamo la lampadina, lasciamo i nostri amici e iniziamo a muoverci lungo t’. La luce tocca lo specchietto S dopo un intervallo di tempo t’ uguale a 1. A quel punto torna indietro e arriva sulla lampadina dopo un intervallo di tempo nuovamente uguale a 1. Il tempo totale di andata e ritorno è uguale a 2 (come abbiamo provato e riprovato varie volte). Che spazio abbiamo percorso? Beh, basta controllare sull’asse delle x’. La luce è arrivata fino a una x’ = 1 (freccia rossa verso destra) e poi è tornata indietro fino a x’= 0 (freccia rossa verso sinistra). Spazio percorso: 1 + 1 = 2. Velocità determinata c = 2/2 = 1. Perfetto, tutto è funzionato perfettamente nel nostro sistema in movimento e ne siamo molto contenti.
I nostri amici, invece, non sono affatto d’accordo. Loro misurano le grandezze sul loro sistema di riferimento nero (fermo). Quando la luce arriva sullo specchietto S, misurano un tempo t =2. Poi la luce torna indietro e quando ha finito il suo percorso misurano un tempo totale t = 2.5. Essendo sicuri che l’asta ha una lunghezza uguale a 1 non possono che concludere che la velocità della luce è uguale a 2/2.5 = 0.8. E iniziano a prenderci in giro… Bastava però che ragionassero un po’ meglio sullo spazio percorso visto dal loro sistema di riferimento.
Mettiamoci sull’asse delle x e vediamo come si è spostata la luce. Beh… aspettando che la luce arrivi in S sono costretti ad ammettere che misurano una x = 2 (freccia nera verso destra). Accidenti! Meno male che quando ritorna nella posizione della lampadina la x vale solo 1.5. Al ritorno, dunque, il percorso misurato è stato solo di 0.5. Basta allora sommare 2 a 0.5 e si trova che lo spazio totale percorso dalla luce nel loro sistema di riferimento è uguale a 2 + 0.5 = 2.5. La velocità della luce vista dal loro sistema è quindi c = 2.5/2.5 = 1. Il risultato è lo stesso ottenuto da noi che stiamo viaggiando. La velocità della luce è effettivamente sempre la stessa!
Possiamo ritrovare questo risultato facendo compiere l’esperimento dagli amici fermi, mentre noi viaggiamo. La figura è adesso la Fig. 3. Per i nostri amici fermi, la luce si muove verso destra fino a x = 1 e poi torna indietro fino a x = 0. Quanto tempo ha impiegato? Beh… banale: un intervallo di tempo uguale a 1 per raggiungere S e un altro intervallo uguale a 1 per tornare indietro. Tempo totale uguale a 2. Distanza totale percorsa uguale a 2. Conclusione: c = 2/2 = 1. Perfetto nuovamente!
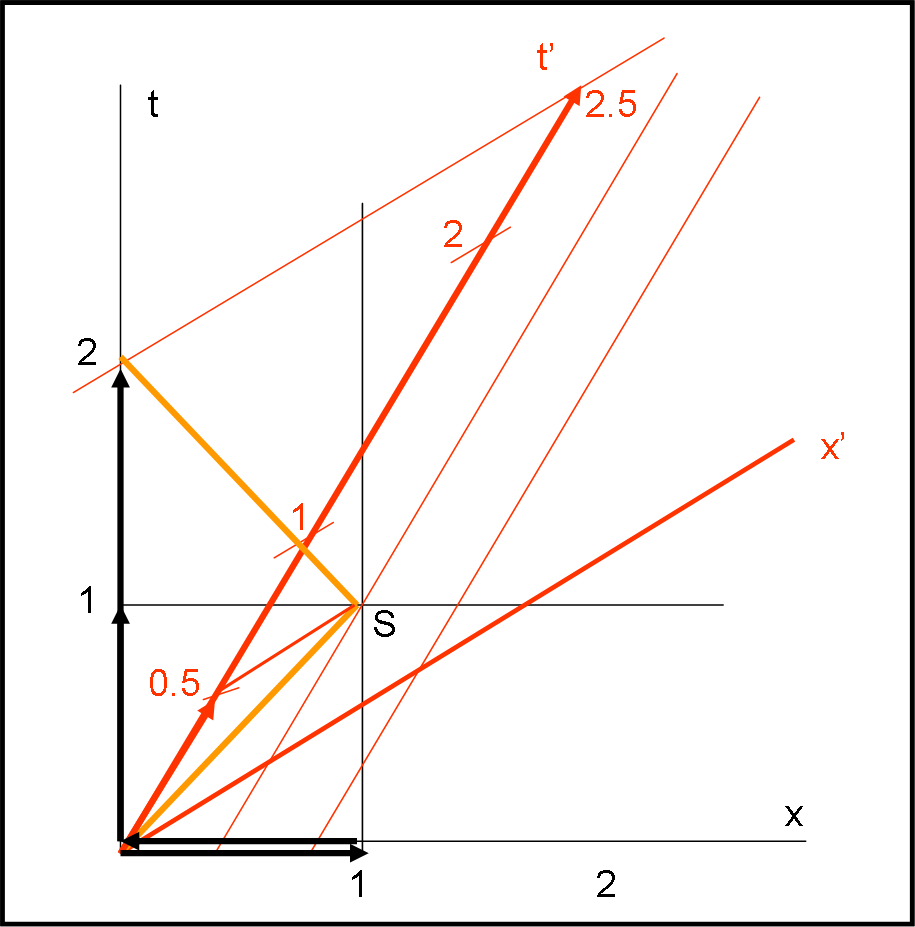
Misuriamo l’esperimento fatto dai nostri amici fermi mentre stiamo viaggiando a v = 0.6. Ovviamente, inseriamo nuovamente le linee parallele a x’. Quando la luce raggiunge S noi misuriamo un tempo t’ = 0.5. Per tornare indietro, però, il tempo si allunga e alla fine misuriamo un tempo totale uguale a 2.5. La stessa cosa che era capitata ai nostri amici quando eravamo noi a fare l’esperimento. La nostra meraviglia durerebbe un attimo se calcolassimo anche noi lo spazio percorso dalla luce del nostro sistema di riferimento.
Lo vediamo utilizzando la Fig. 4. Le misure dobbiamo farle sull’asse x’, ovviamente… L’andata è rappresentata dalla freccia rossa verso destra e noi misuriamo uno spazio x’ = 0.5. Poi la luce torna indietro e dobbiamo aspettare che essa arrivi nuovamente al punto d’inizio. Si vede benissimo che il percorso è molto lungo e alla fine misuriamo x’ = -1.5. A noi non interessano i segni meno della x’, dato che vogliamo calcolare delle distanze. Dobbiamo allora sommare i due percorsi misurati, ossia 0.5 e 2 (ritorno da + 0.5 a -1.5). Per calcolare la velocità della luce non ci resta che dividere lo spazio per il tempo e otteniamo c = 2.5/2.5 = 1.
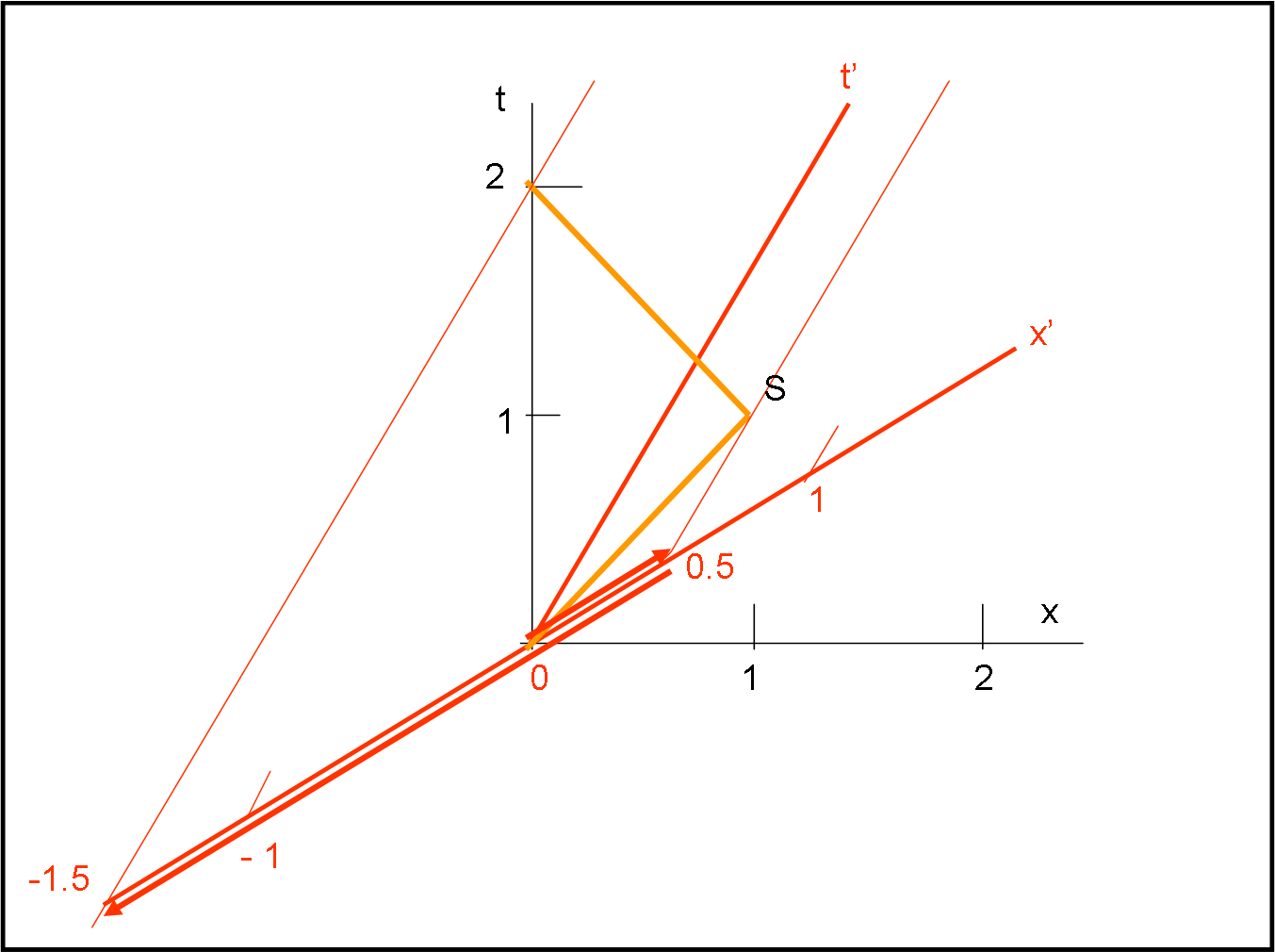
Meno male! La velocità della luce rimane effettivamente sempre la stessa, comunque e dovunque si misuri.
Abbiamo adottato un sistema molto intuitivo e rapido che nasconde la vera problematica che ormai conoscete molto bene e che si riferisce sempre e comunque alla relatività della simultaneità. In qualche modo il problemino può ricordare il paradosso dei gemelli… Potremmo anche inserire nel discorso la contrazione delle lunghezze, ma direi che non è il caso di complicare una soluzione estremamente semplice e immediata. D’altra parte, sia la dilatazione dei tempi che la contrazione delle lunghezze nascono entrambe dalla relatività della simultaneità…
Come al solito, il nostro Paolo (che sa disegnare molto bene e meglio di me) ha già risolto il problemino. Spero che anche chi non è capace a inviare disegni nei post (io riesco a farlo perché posso inserirli direttamente nell’articolo… se no non ne sarei capace!) si diverta a provare e a controllare solo dopo il risultato.
Bene! La prossima volta accenneremo al significato profondamente fisico del diagramma di Minkowski e vedremo come’è capace di separare il presente, il futuro e il passato e quali vincoli pone agli eventi del Cosmo. Insomma, ne vedremo delle belle! Poi ci fermeremo un attimo e cercheremo di completare momento angolare e decadimento radioattivo. Infine, via di nuovo con la RR per cercare di arrivare in modo semplice alla celeberrima E = mc2.






14 commenti
Se può servire, qualche piccola informazione per costruire e postare delle figure.
.........................................................Costruire figure e grafici cartesiani:
Metodo 1
Bastano due squadre ed una carta millimetrata sia per realizzare gli assi cartesiani, sia per disegnare rette inclinate. Basta ricordare che l'inclinazione di una retta può essere espressa come il rapporto m= y/x, quindi per esempio se m=10/6, basta trovare il punto che corrisponde a 10 quadratini misurati sull'asse y e 6 sull'asse x, congiungendo questo punto con l'origine degli assi posso disegnare la retta con la giusta inclinazione (m=y/x = t/x).
Se si usano invece gli angoli basta un normale goniometro.
Una volta realizzata l'immagine basta uno scanner per trasformarla in immagine digitale, in formato jpeg.
Metodo 2
Lo stesso procedimento si può realizzare usando un software grafico..... io uso Photoshop CS2, che uso come se fosse una carta millimetrata .
Indico al software di mostrare una griglia (visualizza: griglia), uso come forma le linee (a cui si può dare una punta trasformandoli in vettori), le sposto, le inclino (con trasformazione: ruota), e costruisco il grafico usando lo stesso metodo indicato prima.
Alla fine salvo l'immagine in jpeg.
Ovviamente lo stesso procedimento si può realizzare usando software grafici diversi da Photoshop.
...........................................................Postare le immagini:
Basta caricare l'immagine su uno dei tanti server gratuiti, e poi copiare e incollare nel testo del messaggio il link dell'immagine.
Ci sono diversi servizi gratuiti in rete che offrono la possibilità di caricare gratuitamente immagini e figure, anche se in genere bisogna iscriversi (senza pagare nulla).
Io ne indico tre, ma le opportunità sono svariate dato che le immagini da caricare non pesano molto (sono solo figure):
http://www.astrobin.com/
http://postimage.org/?lang=italian (vi consiglio si spuntare normale e non adulti)
https://imageshack.us/signup
Ovviamente vanno benissimo anche altri servizi on line che consentono di caricare e archiviare immagini.
Spero possa essere utile.
Paolo
grazie Paolo!!!
Ho fatto anche io qualche disegnino (ho imparato come farli), anche se ormai è già stata pubblicata la soluzione.
Il primo è la soluzione del quiz:
http://www.webalice.it/lottisimone/1.jpg
Il secondo fa vedere la dilatazione dei tempi e la contrazione delle lunghezze visti da entrambi i sistemi:
http://www.webalice.it/lottisimone/2.jpg
Dovrebbero essere abbastanza corretti, ovviamente non sono fatti benissimo dato che mancano di molti “abbellimenti”.
Vorrei fare una domanda a riguardo, dato che è un dilemma che da un po’ mi assale.
Abbiamo dimostrato in questo quiz che la velocita della luce è la stessa indipendentemente dal moto della fonte o dal moto del sistema dal quale la si misura.
Ma, è una caratteristica intrinseca della luce, o qualsiasi sistema che andasse alla velocità della luce (anche se impossibile) si comporterebbe come la luce?
Oppure al contrario se la luce andasse a una velocità inferiore di 300000 Km/s (cosa che si può fare, dato che dipende dal mezzo di propagazione), la luce si comporterebbe come un qualsiasi altro sistema in moto o la sua velocità rimarrebbe la stessa comunque e dovunque la si misuri?
In poche parole è la luce ad essere speciale, o è il fatto che solo lei può andare a 300000 Km/s nel vuoto (dato che non ha massa)?
Non so se sono stato chiaro, in caso contrario dimmelo e provo a spiegarmi meglio.
Grazie
Ciao
Ciao Simone.
Quella che segue NON è la risposta al tuo dubbio ma la MIA interpretazione del tuo dubbio.
Non vorrei suscitare nuovamente le ire di Enzo!!
Anch'io, come te, attendo la risposta ufficiale per capire dove la mia idea è lacunosa e/o totalmente errata.
Uso l'indicativo solo per non dover continuamente ricorrere a congiuntivi e condizionali, non perchè le cose stiano come dico io!
Bene, io ho capito quanto segue. Non chiamo in causa la QED ma mi rifaccio ad una visione classica.
La luce, come noto, non è altro che radiazione elettromagnetica e quest’ultima non è altro che la “somma” di un campo elettrico e di un campo magnetico intimamente connessi che viaggiano di conserva, ciascuno oscillante lungo un proprio piano: i due piani risultano ortogonali.
La radiazione elettromagnetica viaggia in un mezzo di propagazione, quale che sia: vuoto, acqua, vetro, quello che si vuole. Si sa che, nel vuoto, la velocità di propagazione della radiazione elettromagnetica vale c.
Cosa accade quando la luce (uso questo termine per brevità) passa dal vuoto ad un mezzo diverso, inevitabilmente più denso? Il campo elettromagnetico della luce interagisce con i campi elettromagnetici degli atomi che compongono il mezzo. L’intensità di questa interazione è funzione della frequenza dei campi interagenti: siccome un “raggio” luminoso è composto di diverse frequenze, ciascuna di esse seguirà un diverso destino, subendo una maggiore o minore interazione. Il valore MEDIO della velocità di propagazione del campo RISULTANTE è inferiore a c. Nel caso di un raggio laser (cioè monocromatico) incidente, l’interazione, e quindi la velocità di propagazione, dipende dalla frequenza del raggio.
La cosa interessante è che negli spazi che separano un atomo dall’altro, spazi …. siderali visto che tutti i mezzi sono fatti soprattutto di vuoto, il “raggio” luminoso viaggia più o meno indisturbato conservando la sua velocità c.
Ciò che noi osserviamo macroscopicamente è il fenomeno della rifrazione (cambiamento di direzione) che ciascuna frequenza subisce nel moto attraverso il mezzo. Se il mezzo è una struttura ordinata a ciascuna frequenza competerà un diverso e definito angolo di rifrazione.
Credo si possa dire che c è la velocità di propagazione dei campi elettromagnetici quando non devono interagire con altri campi elettromagnetici che li disturbano e deformano in vario modo.
Questa interazione riguarda anche i raggi luminosi che si propagano liberamente nello spazio. Due raggi luminosi identici e sovrapposti propagantisi nella stessa direzione si annulleranno se in opposizione di fase: in questo caso l’interazione dei campi elettromagnetici avrà prodotto un’annichilazione (velocità di propagazione pari a 0).
Se i raggi di cui sopra non fossero in opposizione di fase si otterrebbe un raggio risultante propagantesi ancora con velocità c. Detto raggio avrebbe però ampiezza, frequenza e lunghezza d’onda diversi da quelli originari: si tratterebbe insomma di comporre le due onde interferenti.
penso di avere compreso il dubbio di Simone. Niente può andare alla velocità della luce, per cui puoi considerarla come la velocità del fotone nel vuoto. Il limite è quello del parametro velocità, ma è anche vero che nient'altro che il fotone può raggiungere quel limite. Il succo è che essa non può essere sommata o sottratta, per sua stessa definizione, e quindi deve rimanere costante per ogni sistema.Al di là di tanti discorsi relativi al mezzo che attraversa, noi stiamo discutendo del vuoto e quindi non vi è niente che può frenare la luce. Nel diagramma di Minkowski si considerano movimenti nel vuoto e quindi il fotone non trova nessun intoppo. Che la velocità del fotone sia costante è un dato di fatto dimostrabile sperimentalmente e diventa l'ipotesi di partenza di tutta la RR.
Riguardo ai tuoi grafici, non capisco bene (nelle prime due) quale sia il percorso della luce (non certo il trattino bianco più spesso).
Oh finalmente qualcun altro che inserisce figure... speriamo che questa prassi si diffonda... (vi assicuro che per capire il diagramma di Minkowski bisogna provare a usarlo, disegnando).

Per quanta riguarda la tua domanda, in attesa di una risposta da parte di Enzo, se non ho capito male per C si intende la velocità della luce nel vuoto.
Prova e vederla così: C è da intendersi come la velocità massima con cui un'informazione può viaggiare nell'Universo.
Un osservatore può accorgersi di un evento solo se l'informazione a questo riferito può giungere fino a lui, ossia se questa viaggiando ad una velocità C può raggiungerlo in un certo tempo oppure non potrà mai raggiungerlo (l'informazione dovrebbe viaggiare più veloce di C).
Se rallenti un fascio di luce, facendogli attraversare un mezzo più denso (qui bisognerebbe entrare le merito di come la luce interagisce con atomi ed elettroni, tra assorbimenti e riemissioni di fotoni), ovviamente la "velocità" del fascio di luce è diversa da C, ossia ben al di sotto del limite massimo a cui può viaggiare l'informazione.
Presumo che dovresti trattare il fascio di luce “rallentato” dal mezzo denso, come un qualunque “punto” in movimento ad una velocità V misurata dal sistema di riferimento (che puoi anche considerare fermo).
Ovviamente meglio prendere con le pinze questa mia risposta.....
Paolo
Scusa Simone... non ero riuscito a vederle!!! Cambiando angolazione ho visto le linee sottili rosse scuro. Come non detto!!!!!!
Ringrazio sia Paolo che Alvy per la risposta, e ovviamente ringrazio anche Enzo.
La mia era una domanda più pratica che altro, non volevo addentrarmi in discorsi particolari…o di mezzi di propagazione vari.
Come ha detto Enzo “nel diagramma di Minkowski si considerano movimenti nel vuoto e quindi il fotone non trova nessun intoppo” …ovvero è libero di andare alla velocità c.
Ma se, ad esempio, la luce si propagasse a causa del mezzo che attraversa a 0.8*c rispetto a S’, che a sua volta è in moto rispetto a S, da quest’ultimo sistema come viene misurata la luce?
S misura la luce sempre a 0.8*c, oppure bisogna fare la composizione relativistica della velocità?
Tutto qua, lo so che è una domanda particolare e un po’ stupida.
Per quanto riguarda i grafici che ho inserito, ti chiedo scusa Enzo, sono i primi che faccio e quindi non sono chiarissimi.
Mi sono accorto anche io che i colori fanno pena, purtroppo il CAD che uso usa tale combinazione di tonalità, ma volendo si può cambiare…
In più non ho messo descrizioni perché tu avevi già risposto al quiz.
Diciamo che la luce è la linea rossa scuro, mentre il trattino bianco più spesso non è altro che l’asta rigida di lunghezza unitaria che porta sugli estremi la lampadina da una parte e lo specchio dall’altra.
L’ho messa per indicare in quale sistema viene svolto l’esperimento…
Nel grafico di sinistra la luce impiega nel sistema in moto 1s a compiere l’andata di 1 e 1 s per il ritorno di 1, totale 2 s per fare un percorso di 2.
Visto dal sistema fisso impiega 2 s per percorrere 2 dell’andata, e 0.5 per un ritorno lungo 0.5, totale 2.5 s per 2.5 di strada percorsa.
Nel grafico di destra la luce impiega nel sistema fisso 1s a compiere l’andata di 1 e 1 s per il ritorno di 1, totale 2 s per fare un percorso di 2.
Visto dal sistema in moto impiega 0.5 s per percorrere 0.5 dell’andata, e 2 s per un ritorno lungo 2, totale 2.5 s per 2.5 di strada percorsa.
La velocità della luce è in tutti i casi pari a 1.
Dato che ho usato un cad ti garantisco, che una volta impostate le unità di misura, le quote sono abbastanza precise.
Se una unità sul grafico è un millimetro la quotatura è precisa al centesimo di millesimo di millimetro (10 nm).
Ciao e grazie
caro Simone,
il problema che poni è in realtà un non problema... ciò che fa "rallentare" apparentemente la velocità della luce è l'interazione che i fotoni hanno con gli elettroni. Tra un incontro e l'altro non esiste un mezzo. In altre parole, è come se la luce andasse alla stessa velocità sempre, ma ritarda leggermente quando incontra un elettrone. La QED ci dice anche che non è un vero ritardo, ma è uno spostamento che appare come ritardo (fenomeno di scattering). In qualche modo, perciò, la velocità della RR è sempre la stessa, mentre vanno introdotti fenomeni successivi di interazione. Non è giusto pensare alla luce che entra ed esce da un mezzo come a qualcosa che viaggi più lentamente. Essa continua ad avere la stessa velocità che supporta le ipotesi della RR, ma sono i fenomeni tra particelle che devono essere studiati su questa base. Spero di essere stato chiaro...
Ti ringrazio Enzo, sei stato chiarissimo, era proprio questo che volevo sapere, hai centrato il punto.
Il tuo commento andrebbe incorniciato e messo in evidenza, magari inserito in un articoletto…
Spero che sia stato utile anche ad altri.
Anche Alvy aveva detto più o meno la stessa cosa.
Quindi la luce rispetta sempre e comunque il postulato della RR della costanza di velocità …diciamo che è la sua caratteristica intrinseca valevole sempre.
Se appare “rallentata” è perché subentrano altri fattori, che tu hai spiegato.
P.s i grafici vanno bene?
Ottimo Simone! Comprese le figure!
salve ,
ipotizziamo un sistema di riferimento lungo a piacere , nella meta' della lunghezza si sincronizzano 2 orologi , uno si porta ad un estremo e il secondo all'altro estremo , il sistema si muove a velocita' v in una direzione , dalla direzione opposta parte un raggio di luce , il raggio colpisce il primo orologio e lo ferma , poi colpisce il secondo e lo ferma , intanto il secondo orologio si e' spostato verso il raggio incidente quindi sara' colpito e arrestato prima di quando fosse in quiete.
Conoscendo la distanza tra i due e il tempo (differenza tra gli orari del primo e secondo orologio) avro'
vluce=distanza/t1-t2 > 300.000 km/sec ???
caro Sabato,
la velocità della luce non si somma o si sottraea a nessun'altra velocità. La velocità è la stessa in ogni sistema di riferimento. Quindi lo è anche all'interno del sistema in moto, il che vuol dire che si possono considerare fermi i due orologi e tutto il loro sistema. La luce colpisce il primo e poi colpisce il secondo alla giusta distanza (lui non si è mosso!). Siamo molto vicini sll'esperimento dell'orologio di luce...