Categorie: Fenomeni astronomici Meccanica Celeste
Tags: allineamenti planetari congiunzioni opposizioni periodo sinodico satelliti galileiani
Scritto da: Vincenzo Zappalà
Commenti:16
C’è allineamento e allineamento. 2 **
Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento
E’ già risultato ovvio dalle risposte al quiz che l’esistenza di risonanze di moto medio può essere gioia e dolore per chi cerca di ottenere allineamenti non solo frequenti, ma addirittura periodici. Ricordiamo ancora che, mettendoci nel caso di orbite perfettamente circolari e complanari, eliminiamo i vari effetti mareali e trascuriamo quelli dovuti a eventuali perturbazioni reciproche, anche se debolissime.
Prima di analizzare qualche semplice caso, come quello dei primi tre satelliti galileiani, introduciamo un periodo particolarmente importante: il periodo sinodico di un pianeta rispetto a un altro.
Esso è fondamentale, dato che è l’unico che può essere osservato direttamente.
Consideriamo la Terra e Marte, per esempio. Conosciamo il periodo siderale della Terra (ossia quello effettivo di rivoluzione attorno al Sole) attraverso osservazioni che ci permettano di vedere una certa stella lontana nella stessa posizione precedente. L’intervallo di tempo tra le due osservazioni ci regala il periodo di rivoluzione intorno al Sole (vi sono anche altri periodi, ma che -per adesso- possiamo tralasciare).
Non avendo ancora mandato uomini su Marte, non possiamo aspettarci che essi ci diano la stessa informazione sul pianeta rosso. Tutto ciò che possiamo fare è osservare quando Marte si viene ad allineare perfettamente con noi e il Sole (ossia si trova all’opposizione). L’intervallo di tempo tra due opposizioni, ossia tra due allineamenti, prende proprio il nome di periodo sinodico.
Senza bisogno di sapere le leggi di Keplero, basta questa informazione per ricavare il periodo di rivoluzione di Marte attorno al Sole.
Disegniamo la semplice Fig. 2.
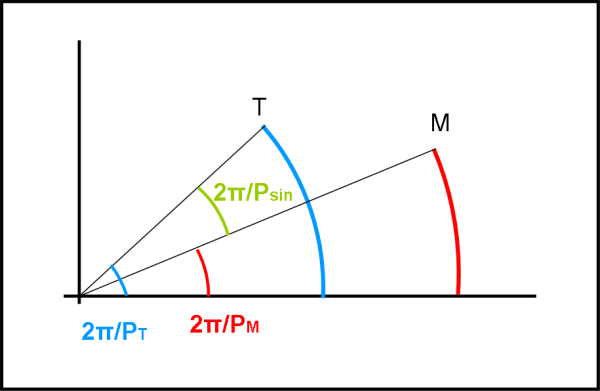
La Terra rivolve più velocemente di Marte e, nel caso di orbita circolare, possiamo scrivere che la sua velocità angolare è costante e vale 2π/PT. Velocità angolare non vuole dire altro che angolo percorso nell’unità di tempo. Marte, più lento, nella stessa unità di tempo ha, invece, una velocità angolare data da 2π/PM. La Terra lascia Marte dietro di sé e inizia il suo giro attorno al Sole fino a compierlo completamente. E’ passato un tempo PT.
Ovviamente, però, in quella posizione, Marte non si troverà più nella stessa posizione dell’anno precedente. Anche se più lentamente si è spostato nella sua orbita. La Terra, per raggiungerlo deve allora percorrere un certo angolo supplementare. In altre parole, per ritrovarsi allineata con Marte e Sole deve girare ancora un po’. Di quanto dovrà girare? Proprio della differenza tra il suo angolo percorso nell’unità di tempo e quello percorso nell’unità di tempo da Marte. Questo angolo corrisponde al movimento della Terra relativo a Marte ed è proprio dato da 2π/Psin, dove Psin è l’intervallo di tempo necessario alla Terra per ritrovarsi allineata con Marte e il Sole, ossia l’intervallo tra due opposizioni, o -ancora- il periodo sinodico di Marte relativo alla Terra. Si può scrivere la banale formula:
2π/Psin,M = 2π/PT - 2π/PM …. (1)
Conoscendo PT e osservando Psin si può ricavare PM
Se, invece, applicassimo lo stesso tipo di procedimento a un pianeta interno come Venere, ci troveremmo di fronte a un cambiamento di segno. Venere va più forte della Terra. La formula precedente diventa:
2π/Psin,V = 2π/PV - 2π/PT …. (2)
Ovviamente, per due pianeti si ha sempre un allineamento (o esterno o interno) a ogni periodo sinodico.
Torniamo a Marte e immaginiamo, adesso, di aggiungere un terzo pianeta, per esempio Giove. La formula precedente ci permette di sapere quando avverrà un futuro allineamento tra Terra e Giove. Tuttavia, dopo un periodo sinodico di Marte NON ci sarà sicuramente Giove allineato, dato che il suo periodo sinodico è diverso. L’unica cosa da sperare è che a furia di girare attorno al Sole succeda che un multiplo esatto del periodo sinodico di Marte coincida perfettamente con un multiplo esatto del periodo sinodico di Giove. Ossia è necessario che trascorra un tempo t dato da:
t = m Psin,G = n Psin,M …. (3)
con m e n numeri INTERI. (N.B.: E se non lo fossero mai…?)
Bene, abbiamo già anticipato in parte il risultato finale, in modo molto formale, e possiamo tornare all’inizio e considerare il caso di pianeti o satelliti (o quello che volete) con periodi che stanno in risonanza tra loro. Questo già ci assicura che i periodi stanno tra loro come numeri interi semplici. Prendiamo quella forse più famosa che è la risonanza di Laplace, ossia tale che il rapporto tra i periodi di rivoluzione dei tre oggetti celesti stiano tra loro come i numeri 1, 2 e 4. Siamo nel caso di Io, Ganimede e Europa
I tre satelliti di Giove hanno periodi PI, PE e PG tali che:
PI/PE = 1/2
PI/PG = 1/4
Consideriamo come unità di misura del tempo il periodo di rivoluzione di Io attorno a Giove. Per cui
PI = 1
PE = 2
PG = 4
D’ora in poi, per una necessità di semplicità che risulterà evidente più in là, assumiamo che all’istante iniziale (t = 0) i tre oggetti siano perfettamente allineati.
La domanda è: “Dopo quanto tempo torneranno a essere allineati?”
Il caso è talmente semplice che possiamo risolverlo graficamente, come mostrato in Fig. 3.
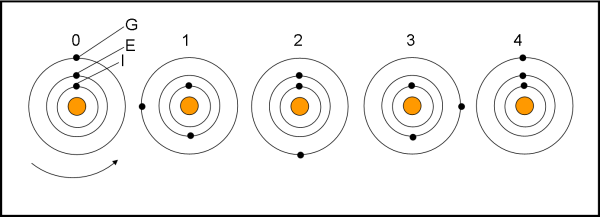
Dopo un giro esatto di Io, Europa si trova allineata in direzione opposta rispetto a Giove, avendo percorso solo 1/2 della sua orbita, e Ganimede spostato verso sinistra (in quadratura) avendo percorso solo 1/4 della sua orbita. Dopo due rivoluzioni di Io, Europa torna a essere allineata con lui dalla stessa parte di Giove, mentre Ganimede si trova a 180°. Dopo tre rivoluzioni Io ed Europa si trovano in posizioni opposte rispetto a Giove e Ganimede spostato verso destra. Alla quarta rivoluzione di Io tutto torna esattamente com’era all’istante 0. Ne segue che sono necessarie quattro rivoluzioni di Io per riottenere l’allineamento. Va notato che abbiamo semplificato l’intera faccenda avendo trascurato la pur piccola eccentricità orbitale e la precessione del perielio. Ma per i nostri scopi possiamo permetterci questo e altro.
L’intervallo t tra due allineamenti dei tre oggetti, dalla stessa parte rispetto a Giove, è dato quindi da:
t = 4 rivoluzioni di Io
Possiamo ottenere lo stesso risultato senza bisogno di fare figure che potrebbero diventare lunghissime cambiando il tipo di risonanza? Sicuramente sì: basta ricordare la (1) e la (3), ossia utilizzare i periodi sinodici.
Determiniamo i periodi sinodici di Europa e Ganimede rispetto a Io. Consideriamo ancora come unità di tempo il periodo di rivoluzione di Io. La (1) ci dice:
2π/Psin,E = 2π/PI - 2π/PE
1/ Psin,E = 1/1 – 1/2
1/Psin,E = 1/2
Psin,E = 2
1/Psin,G = 1 – 1/4
Psin,G = 4/3
Ovviamente, per come è definito, il periodo sinodico di un oggetto, più lontano e più lento, risulta più corto di quello di un oggetto più vicino e veloce. Se l’oggetto lontano fosse praticamente fermo, il periodo sinodico sarebbe praticamente uguale al periodo di Io.
Ricordando la (3), per avere un nuovo allineamento, deve essere:
m Psin,G = n Psin,E …. (4)
m 4/3 = n 2
m/n = 2·3/4 = 6/4 = 3/2
Esistono due numeri interi m e n tali che sia soddisfatta la relazione (4)? Sì, e i più piccoli sono proprio:
m = 3
n = 2
Ne segue che l’intervallo di tempo tra due allineamenti dei tre satelliti sarà dato da:
t = 3 Psin,G = 2 Psin,E = 3·4/3 = 2·2 = 4 periodi di rivoluzione di Io
Come volevasi dimostrare
Fate pure altri casi particolari per prendere dimestichezza con il periodo sinodico. Magari, potreste calcolarvi i periodi sinodici di tutti i pianeti rispetto alla Terra oppure i periodi sinodici di tutti i pianeti rispetto a Nettuno. La prossima volta cercheremo di fare come Taylor, ossia cercare di ottenere il tempo t con approssimazioni successive.
Se siete interessati all’argomento, non potete perdervi il primo articolo e quelli che seguono
http://www.
http://www.
http://www.
nonché le immagini di un raro allineamento vissuto in diretta
http://www.
16 commenti
Non vorrei fare quello sempre alla ricerca dell'errore per forza, ma subito dopo Figura 2 hai scritto "La Terra rivolve più lentamente di Marte [...]".
fai pure Michael! Posso solo ringraziarti per aiutarmi a scovare gli errori di un vecchio che sta forse rimbambendo un po' troppo...
E' un circolo oppure no? E, quindi, viva la collaborazione!
Caro Michael,
volevo aggiungere che, come vedi, non elimino i commenti di questo tipo (nasconderei velocemente i refusi vari). Preferisco lasciarli per spingere tutti a comunicarmeli immediatamente!!!
Nessuno è perfetto e io per primo...
Non ho mai neanche lontanamente sospettato che lo facessi. ;)
L'ho ben capito che sei onesto.
grazie Michael...
d'altra parte, che male c'è a sbagliare? Il male si fa solitamente quando si cerca di nascondere le proprie limitatezze...
volevo chiedere una cosa relativamente alla possibilità di avere l'eguaglianza:
t = m Psin,G = n Psin,M (3)
a)è sempre possibile esprimere i periodi sinodici in frazioni (ovvero numeri razionali)?
b)oppure è sempre possibile esprimere i periodi di rivoluzione in frazioni?
se è vera la a) e vera anche la b) e viceversa perchè in ogni caso con la (2) abbiamo operazioni di somme e prodotti
con i numeri razionali (il π si semplifica) e quindi un numero razionale.
perchè sia vera la 3) con n e m interi, basta che il rapporto fra i sinodici di marte e giove sia un numero razionale,
per cui anche il rapporto fra m e n diventa un numero razionale, ed è possibile trovare n e m.
spesso vedo che si usa scrivere i periodi come frazioni, per esempio
Marte 1,881 anni oppure 1881/1000, ma non so se il periodo è in origine un numero razionale
caro Umberto,
hai perfettamente capito qual'è il vero problema per periodi qualsiasi. Hai anticipato ciò che dirò nel prossimo articolo. Non è assolutamente detto che i periodi siano numeri razionali...
Caro Enzo, ho provato ad usare le formulette che hai inserito, rimaneggiandole leggermente per trovare i periodi sinodici di tutti i Pianeti del Sistema Solare (più Plutone, che mi sta simpatico) rispetto alla Terra.
Partendo dalla formula: 2π/Psin,M = 2π/PT - 2π/PM , la trasformo in una formula generale valevole per tutti i pianeti esterni (quelli con velocità minore del pianeta di riferimento):
2π/Psin,est = 2π/PT – 2π/Pest
1/Psin,est = 2π/2π PT – 2π/2π Pest = 1/Psin = 1/PT - 1/Pest
1/Psin, est = (PM – Pest)/PT Pest
Psin = PT Pest/(Pest – PT)
Per i Pianeti interni, basta invertire i segni della sottrazione, ossia:
2π/Psin,int = 2π/Pint – 2π/PT
1/Psin,int = 2π/2π Pint – 2π/2π PT = 1/Pint – 1/PT
1/Psin, est = (PT – Pint)/Pint PT
Psin, est = Pint PT/(PT – Pint)
Basta applicare queste due semplici formulette per calcolare il Periodo Sinodico.
La Figura oltre a calcolare i periodi Sinodici di tutti i pianeti riporta anche i loro periodi orbitali:
http://www.astrobin.com/full/187783/M/
Se poi qualcuno si sente un po' nettuniano
può consultare la tabella che mostra i Periodi Sinodici dei Pianeti rispetto a Nettuno. 
http://www.astrobin.com/full/187783/N/
Ovviamente conoscendo il Periodo Sinodico (durata tra un opposizione e l'altra) e il Periodo Orbitale della Terra o di qualunque altro pianeta si prenda a riferimento, è facile trovare il Periodo orbitale del Pianeta:
1/Psin,est = 1/PT - 1/Pest
1/Pest =1/PT - 1/Psin
1/Pest = (Psin - PT)/PT Psin
Pest = PTPsin/(Psin - PT)
Con i Pianeti interni cambia il segno dei termini della sottrazione.
Infine, ho tentato (ma dei risultati sono meno sicuro rispetto a quelli precedenti
) di trovare ogni quanto possono allinearsi: Terra; Marte, Giove e Saturno...
Prima provo con Terra, Marte e Giove, usando i loro periodi sinodici espressi in giorni (Marte 780; Giove 399; Saturno 378) e partendo dalla formuletta:
t = m1 (Psin,G) = n1 (Psin,M)
m1/n1 = Psin,M/ Psin,G
m1/n1 = 780/ 399 sono entrambi divisibili per 3
m1/n1 = (780/3)/(399/3) = 260/133
Per verificare se i valori trovati di m e n sono corretti e ogni quanto tempo occorre ai tre Pianeti per allinearsi verifico l'equazione iniziale:
t = m1 (Psin,G) = n1 (Psin,M) = 260 (399) = 133 (780)= 103740 = 103740 =284 anni
m1 (Psin,G) = 260 (399) = 103740 giorni =284 anni
n1 (Psin,M) = 133 (780)= 103740 giorni =284 anni
Sembra funzionare......
Provo a confrontare Saturno con Terra e Marte e ricavare di nuovo i valori di m e n:
m2/n2 = Psin,M/ Psin,S
m2/n2 = 780/ 378 sono entrambi divisibili entrambi per 6 = 130/63
m2/n2 = (780/6)/(378/6) = 130/63
Ovviamente ho ottenuto due diversi valori di m ed n..... prima avevo m1/n1 = 260/133, ora ho m2/n2 = 130/63
Mi sono chiesto come conciliare questi due diversi rapporti....
Esistono dei multipli (numeri interi) che soddisfano entrambe le relazioni?
Anche in questo caso penso sia necessario trovare un multiplo comune.... il problema non è come “conciliare” i numeratori (uno è il doppio dell'altro), ma i denominatori, ossia 133(n1) e 63(n2).
Entrambi i numeri però sono divisibili per 7:
133/7 = 19......................................63/7 = 9
133/19= 7.......................................63/9=7
133/19 = 63/9
133 (9) = 63 (19) = 1197
Quindi se moltiplico n1 per 9 e n2 per 19 dovrebbero allinearsi tutti e quattro i pianeti, ovviamente se moltiplico il denominatore per qualcosa devo fare lo stesso anche per il numeratore
260/133 (9/9) = 2340/1197
130/63 (19/19) = 2470/1197
Quindi i nuovi valori che devono assumere sono: m1=2340 m2=2470 n1=n2= 1197
A questo punto per vedere quando i Pianeti sono allineati, dovrebbe valere un'equazione simile:
t = m1 (Psin,G) = n1 (Psin,M)
t = m2 (Psin,S) = n2 (Psin,M)
t = m1 (Psin,G) = n1 (Psin,M) = m2 (Psin,S)
t = 2340 (399) = 933660 giorni =2556,17 anni
t = 1197 (780) = 933660 giorni =2556,17 anni
t = 2470 (378) = 933660 giorni =2556,17 anni
Anche in questo caso sembra funzionare, però non sono sicurissimo di aver semplificato al massimo le relazioni.
.... inoltre ho usato i giorni, che però ho approssimato al numero più vicino, ossia non ho considerato i decimali....
Così sicuramente si paga il prezzo dell'aver approssimato, l'allineamento “perfetto”, ma l'idea (forse errata) che mi sono fatto è che i numeri con decimali si possono trasformare in numeri interi moltiplicando per 10 o sue potenze, ma così l'intervallo tra allineamenti cresce esponenzialmente.
Paolo
Eh sì, caro Paolo,
. E se penso che qualcuno che commette errori marchiani (professionista) cerca in tutti i modi di nascondere la polvere sotto al tappeto e si ostina a non volerlo ammettere... beh... la rabbia sale!
hai proprio ragione... Tutto sta nella precisione dell'allineamento che vuoi ottenete. Più è preciso e più i numeri crescono fino a superare l'età del Sistema Solare...
Se poi vogliamo anche tenere conto delle eccentricità e delle perturbazione... poveri noi!
E purtroppo non c'è programma prefabbricato che ci salvi: anche loro hanno bisogno di fare calcoli e anche loro devono approssimare. Insomma, possiamo stare tranquilli: la tanto temuta bilancia gravitazionale (del tutto assurda) non si verificherà mai...
Vedrai che la prossima volta faremo un'operazione di approssimazione con Venere e Mercurio proprio simile a quanto hai già fatto tu...
Sono proprio contento di vedere quanto ti diverti con questi calcoli. Un abbraccio sincero
Caro Enzo, ho provato a scrivere una raccomandata con ricevuta di ritorno ai vari Pianeti del Sistema Solare per chiedere ogni quanto si allineano tra loro e.... sono stati più disponibili e veloci dell'INAF a rispondermi...
Anche loro sorridono
quando sentono certi racconti privi di fondamento su di loro, che di salire su strane bilance gravitazionali tutti insieme proprio non ne vogliono sapere...
Mi hanno risposto (sempre che io abbia compreso correttamente il loro linguaggio) che anche ad esser benevoli, usando come sistema di misura i giorni (quindi con un errore di tale ordine nelle approssimazioni), per allinearsi tutti insieme (da Mercurio ad Nettuno) serve un numero di anni maggiore dell'attuale età dell'Universo
E a ben guardare, dicono i tre pianeti esterni più vicini, se l'approssimazione è più precisa (usando come unità di misura i minuti), anche il solo l'allineamento Terra-Marte-Giove-Saturno risulta impossibile.
http://www.astrobin.com/full/187783/O
Paolo
PS: il metodo che ho usato per trovare il tempo necessario tra un allineamento e l'altro è quello descritto nel post precedente (ho provato per conferma a far calcolare il MCM ad Excel che sembra confermare i risultati trovati.. ma non si sa mai... sbagliando s'impara!)
scusa Paolo... mentre il risultato finale mi sembra corretto, non capisco cosa significhi il fatto che l'allineamento Terra-Marte (da solo) sia pari a più di duemila anni. L'allineamento tra due soli pianeti si ha sempre ogni periodo sinodico...
Forse ho capito Paolo... tu vuoi che l'opposizione successiva avvenga esattamente come la prima? Beh... non dobbiamo esagerare... Oppure c'è ancora qualcosa che non capisco...?
Mi sa che le virgole possono trarre in inganno .... Gli anni sono due virgola 135 e non 2135 anni .
Paolo
Acci che svirgolata che ho fatto... ho considerato la virgola all'inglese... Come non detto... scusami!!!!
Questi inglesi
:
noi usiamo i punti per indicare le migliaia e le virgole per i decimali, loro il contrario;
noi usiamo il sistema metrico decimale, loro piedi pollici e...
noi usiamo chilogrammi, grammi, ecc, loro libbre, once...
Sembra che ce la mettono tutta per confonderci le idee (o forse siamo noi che ce la mettiamo tutta per confondere le idee a loro) !
Ed a volte riescono a confondersi da soli come è accaduto alla povera sonda Mars Climate Orbit, che nel 1998 si è disintegrata nell'atmosfera marziana, per un errore di conversione (non effettuata) delle unità di misura, per cui invece di collocarsi ad un altezza di 140 Km dal suolo si è collocata da un altezza di soli 57 Km …. ed addio sonda...
Paolo