Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Impostiamo nuovamente il problema dell’allineamento.

Due pianeti rivolvono con velocità angolare ω₁ e ω₂. Ne segue che lo “spazio” percorso, espresso in radianti lungo la circonferenza orbitale, è dato, per un certo istante t qualsiasi, da ω₁t e ω₂t.

La condizione di allineamento, rispetto al Sole, è allora data semplicemente da:

t(ω₁ – ω₂) = h 2π

e quindi l’istante t di allineamento è dato da:

t = h 2π/( ω₁ – ω₂), con h numero intero.

Abbiamo solo detto che si ha allineamento quando la differenza di spazio percorso dai due pianeti è esattamente zero o un multiplo di 2π.

Se consideriamo un terzo pianeta con velocità angolare ω₃, si avrà che l’allineamento con ω₁ si ottiene per:

t = k 2π/( ω₁ – ω₃)

Per ottenere l’allineamento dei tre pianeti è, quindi, necessario che i due tempi t siano uguali, ossia:

h/( ω₁ – ω₂) = k/(ω₁ – ω₃)

h (ω₁ – ω₃) = k (ω₁ – ω₂)

E infine:

(ω₁ – ω₃)/(ω₁ – ω₂) = k/h

Dato che k e h sono numeri interi, il loro rapporto è un numero razionale e tale deve essere anche il primo membro.

Se non esistono particolari risonanze, però, le velocità angolari possono essere qualsiasi. Ad esempio, assumiamo che:

ω₁ = 2

ω₂ = 1

ω₃ = 2 - √2

Il rapporto diventa:

(ω₁ – ω₃)/(ω₁ – ω₂) = (2 – 2 + √2)/(2 – 1) = √2

Purtroppo questo è un numero irrazionale e non potrà mai essere espresso come rapporto tra numeri interi. La conclusione è che non vi sarà mai un allineamento perfetto! Anche semplificando al massimo la problematica, saremmo sempre schiavi delle velocità angolari dei pianeti, le quali non si curano per niente di stare lontane dai numeri irrazionali…

Come si vede facilmente, un perfetto allineamento non è cosa facile da ottenere, soprattutto se cresce il numero dei pianeti coinvolti. Non vi sarà certo sfuggito che le formule usate poco fa sono del tutto analoghe a quelle che facevano uso dei periodi sinodici. Non abbiamo fatto che ottenere un risultato simile con approcci leggermente diversi, anche se solo apparentemente. Non per altro, la volta scorsa avevamo cercato di approssimare i rapporti dei periodi sinodici con rapporti di numeri interi…

Proviamo adesso a impostare il problema dell’allineamento senza curarci del Sole. E’ proprio il tipo di allineamento più comune, come quello che sta capitando in questi giorni e che è già stato catturato dalla nostra Giorgia. D’altra parte, per avere Marte e Venere vicini (uno è esterno e uno è interno), non possiamo certo avere i pianeti dalla stessa parte, con il Sole esattamente alle spalle! Questo tipo di allineamento si calcola in maniera leggermente più complessa, ma del tutto comprensibile. Limitiamoci al caso di due soli pianeti allineati, ossia visti in congiunzione. La situazione è mostrata in Fig. 4.

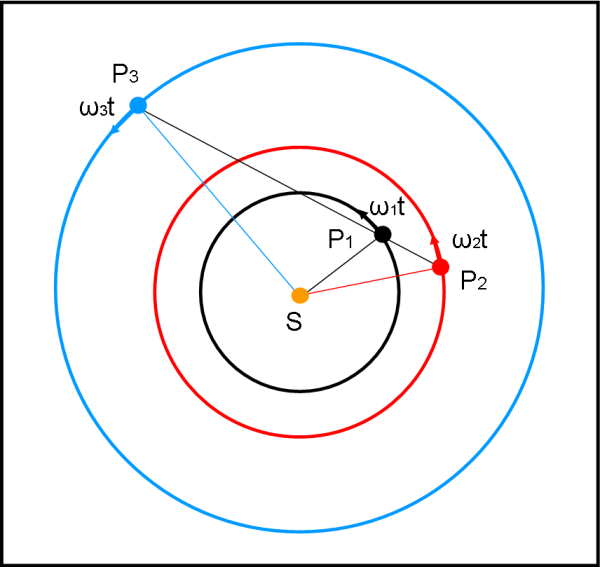
Ricordando il passaggio da coordinate polari a coordinate cartesiane (se avete bisogno di un ripasso andate QUI), un pianeta P, con velocità angolare ω, che è a una distanza r dal Sole (r = raggio della circonferenza orbitale) ha coordinate, istante per istante, date da:

x = r cos (ωt)

y = r sin (ωt)

Applicando le formule ai tre pianeti della figura si ha:

x₁ = r₁cos(ω₁t)

y₁ = r₁ sin(ω₁t)

x₂ = r₂ cos(ω₂t)

y₂ = r₂ sin(ω₂t)

x₃ = r₃ cos(ω₃t)

y₃ = r₃ sin(ω₃t)                ….(1)

E’ immediato stabilire che i tre pianeti risultano allineati (come in figura) solo se la pendenza della retta tra P₁ e P₂ è uguale alla pendenza della retta tra P₂ e P₃.

Questo fatto può espresso facilmente attraverso le coordinate dei tre punti.

La prima pendenza è data da:

(y₂ – y₁)/(x₂ – x₁)

La seconda da:

(y₃ – y₂)/(x₃ – x₂)

E, quindi:

(y₂ – y₁)/(x₂ – x₁) = (y₃ – y₂)/(x₃ – x₂)

Facciamo un po’ di calcoli e scriviamo in altro modo la condizione precedente:

(y₂ – y₁)(x₃ – x₂) = (y₃ – y₂)(x₂ – x₁)

y₂x₃ – y₂x₂ – y₁x₃ + y₁x₂ = y₃x₂ – y₃x₁ – y₂x₂ + y₂x₁

y₂x₃– y₁x₃ + y₁x₂ = y₃x₂ – y₃x₁ + y₂x₁

- y₂x₃+ y₁x₃ - y₁x₂ + y₃x₂ - y₃x₁ + y₂x₁ = 0

(x₁y₂ – x₂y₁) + (x₂y₃ – x₃y₂) + (x₃y₁ – y₃x₁) = 0         …. (2)

Non ci resta, adesso, che sostituire alle x e y le relazioni in funzione dell’angolo e del tempo (ossia le (1))

r₁cos(ω₁t) r₂sin(ω₂t) - r₁sin(ω₁t) r₂cos(ω₂t) +

+ r₂cos(ω₂t) r₃sin(ω₃t) - r₂sin(ω₂t) r₃cos(ω₃t) +

+ r₃cos(ω₃t) r₁sin(ω₁t) - r₃sin(ω₃t) r₁cos(ω₁t) = 0            …. (3)

Per semplificare il tutto bisogna ricordare la formula della sottrazione del seno (si può anche dimostrare, ma per adesso prendiamola per buona), che dice:

sin(a-b) = sin(a) cos(b) – cos(a) sin(b)

Da cui, la (3) diventa:

r₁r₂ sin ((ω₂ - ω₁)t) + r₂r₃ sin ((ω₃ - ω₂)t) + r₁r₃ sin ((ω₁ - ω₃)t) = 0     …. (4)

A questo punto, possiamo eliminare le scomode velocità angolari, dato che, nel caso di orbite circolari e per una conveniente scelta delle unità di misura, abbiamo (Keplero....):

ω²r³ = 1

Ossia:

ω² = 1/r³

ω = 1/r^3/2

 Sostituendo, la (4) diventa:

r₁r₂ sin((1/r₂^3/2-1/r₁^3/2)t) + r₂r₃ sin ((1/r₃^3/2-1/r₂^3/2)t) + r₁r₃ sin ((1/r₁^3/2 -1/r₃^3/2)t) = 0

dividendo tutto per r₁r₂r₃ si ha, infine:

sin((1/r₂^3/2-1/r₁^3/2)t)/r₃ + sin((1/r₃^3/2-1/r₂^3/2)t)/r₁ + sin((1/r₁^3/2 -1/r₃^3/2)t)/r₂ = 0     …. (5)

La parte sinistra della (5), malgrado sembri un guazzabuglio, non è altro che una funzione soltanto di t, dato che i raggi r sono noti. Tutto, quindi, si riduce a trovare gli zeri della funzione, ossia i valori di t per cui essa si annulla. Questi sono proprio gli istanti in cui si ha un allineamento tra i tre pianeti.

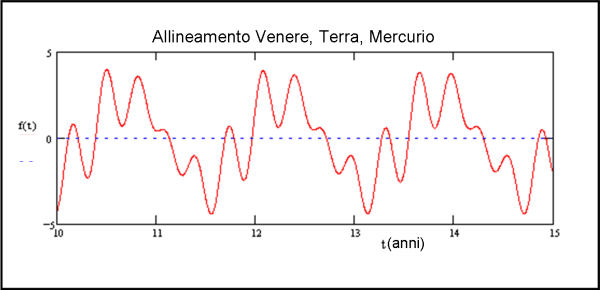
Nel caso di Mercurio, Venere e Terra, si ottiene la curva riportata nella Fig. 5, per un intervallo di 5 anni. Attenzione che nelle soluzioni compaiono anche quelle in cui Marte e Venere stanno a 180° rispetto alla Terra (vi è sempre allineamento…).

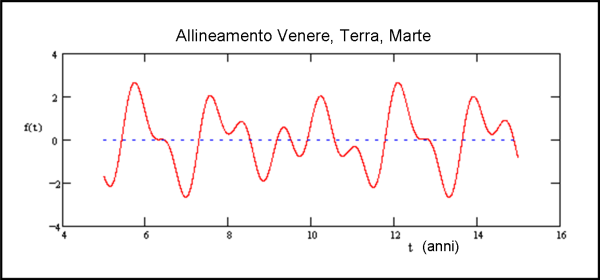
Lo stesso tipo di approccio può essere fatto per altri tre pianeti, ad esempio Venere, Terra e Marte (Fig. 6) e via dicendo.

Passare a quattro pianeti implica una complicazione della funzione che non è il caso di discutere.

Posso consigliare, per chi fosse interessato in modo particolare, di leggere questo articolo che sviluppa una teoria per il calcolo di vari tipi di allineamento con un numero di pianeti crescenti e per diverse ampiezze della zona di cielo che li contiene. Ovviamente, sono sempre calcoli basati su semplificazioni orbitali. Tuttavia, come si può notare, un allineamento totale e abbastanza stretto supera di gran lunga l’età del Sistema Solare.

A questo punto, sapendo di cosa stiamo parlando e delle difficoltà relative all’approssimazione usata per descrivere il sistema planetario, chi vuole può anche utilizzare Stellarium o cose del genere, tenendo comunque conto che anche questi programmi si basano su calcoli e approssimazioni che, per tempi molto lunghi, possono dare risultati completamente privi di senso.

Se siete interessati all’argomento, non potete perdervi gli articoli precedenti

http://www.infinitoteatrodelcosmo.it/2015/10/15/ce-allineamento-e-allineamento-1/

http://www.infinitoteatrodelcosmo.it/2015/10/21/ce-allineamento-e-allineamento-2/

http://www.infinitoteatrodelcosmo.it/2015/10/26/ce-allineamento-e-allineamento-3/

nonché le immagini di un raro allineamento vissuto in diretta

http://www.infinitoteatrodelcosmo.it/2016/02/07/allineamento-planetario-questa-volta-ci-siamo/