Iniziamo, finalmente, il nostro lungo viaggio nel mondo degli integrali. Useremo due modi per definirli, per poi legarli strettamente attraverso un teorema fondamentale. Non abbiate paura, però: il discorso sarà molto semplice almeno fino alla “digestione” completa dei concetti più importanti. Riuscire, poi, a calcolare tutti gli integrali che si vorrebbero, diventa esercizio ben più arduo anche per i professionisti. Si usano vari “trucchi” e le serie ci aiutano. Ma… non corriamo. Cominciamo con qualcosa che è veramente alla portata di tutti: le aree dei rettangoli, dei triangoli e dei trapezi…
N.B.: i primi articoli sugli integrali sono comprensibili e utili a TUTTI, anche a coloro che non sono riusciti a seguire le tantissime lezioni sulla matematica. Vi invito perciò a leggerli ugualmente...

Non posso certamente presentarlo come un quiz… Tuttavia, facciamoci la domanda: “Come si calcola l’aera di un rettangolo?”. La risposta è corale: “Base per altezza o, più semplicemente, lato per lato”. E l’area di un triangolo qualsiasi? Ovvio anche questo: “Base per altezza diviso  due”. E quella di un trapezio? “Somma delle basi per altezza diviso due”. Insomma, su queste cose siamo proprio preparati…

No, non voglio prendervi in giro, ma lasciatemi fare la Fig. 1, relativa al rettangolo. Forse la figura più facile che abbia mai presentato… tuttavia, ci verrà molto utile. Abbiamo utilizzato gli assi cartesiani e tracciato due segmenti paralleli agli assi x e y. Il nostro rettangolo OABC ha un lato uguale a x e l’altro uguale a y e la sua area è xy. Insomma, banalità, veramente banalità.

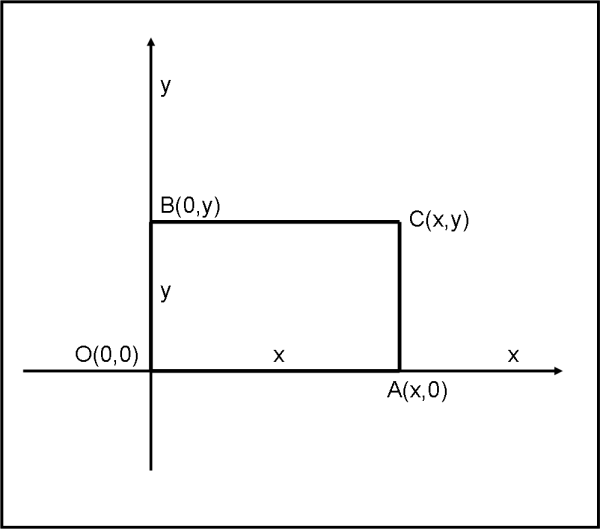
Per rispondere a coloro che vorrebbero vedere chiaramente i legami tra operazioni matematiche e/o geometriche e la fisica applicata, utilizziamo, nuovamente la Fig. 1 (chiamiamola Fig. 2 e ridisegniamola), dove al posto della x inseriamo la variabile t e al posto della y la variabile v. I simboli usati non sono casuali, ovviamente, e sappiamo bene a cosa corrispondono: t rappresenta il tempo e v la velocità. Facciamo, allora, un piccolo salto indietro e vediamo a cosa corrisponde fisicamente la Fig. 2. Beh, non è certo difficile, essa rappresenta il moto di un oggetto con velocità costante v₀.

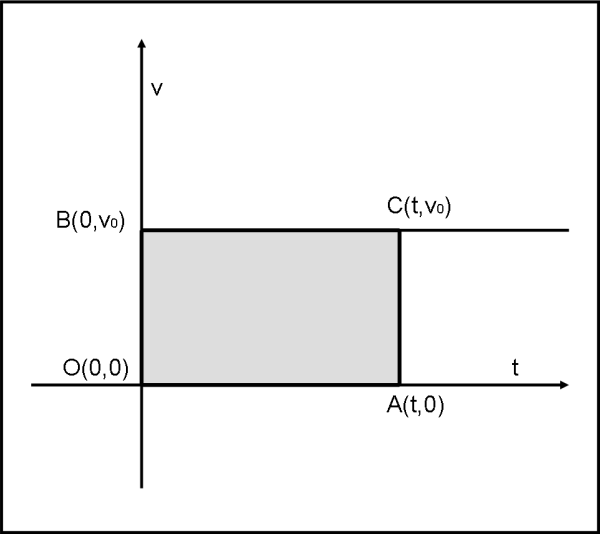
Il grafico, infatti, ci dice che qualsiasi sia il tempo t della misura, la velocità del corpo è sempre la stessa. E’ una situazione così banale? Assolutamente no, dato che siamo nel caso di oggetti che si muovono con velocità costante, ossia di moto rettilineo uniforme. Vi sembra poco? Accidenti, sicuramente no, dato che tutta la relatività ristretta si occupa solo di sistemi di riferimento che seguono questa regola. La Fig. 3 è, quindi, una rappresentazione fondamentale della fisica e non certo un gioco da bambini! Non facciamoci ingannare dalla semplicità e ricordiamo sempre che la Natura lavora in modo semplice.

Voglio tenervi sulle spine e faccio un piccolo salto (chiedendovi, ovviamente, di tenere bene a mente anche quello che abbiamo appena descritto).

Vi ricordate sicuramente come si descrive il moto di un corpo che si muove con velocità costante v₀. Esso descrive una legge oraria (lo spazio percorso in funzione del tempo) che  si scrive:

s = s₀ + v₀t        …. (1)

Dove s₀ è la posizione del corpo al momento in cui faccio partire l’orologio. Se immaginiamo di partire dall’origine (s₀ = 0), la (1) diventa:

s = v₀t       …. (2)

Come si rappresenta quanto appena detto in un diagramma spazio-tempo? Lo vediamo immediatamente nella Fig. 3, dove gli assi rappresentano, adesso, proprio lo spazio s e il tempo t.

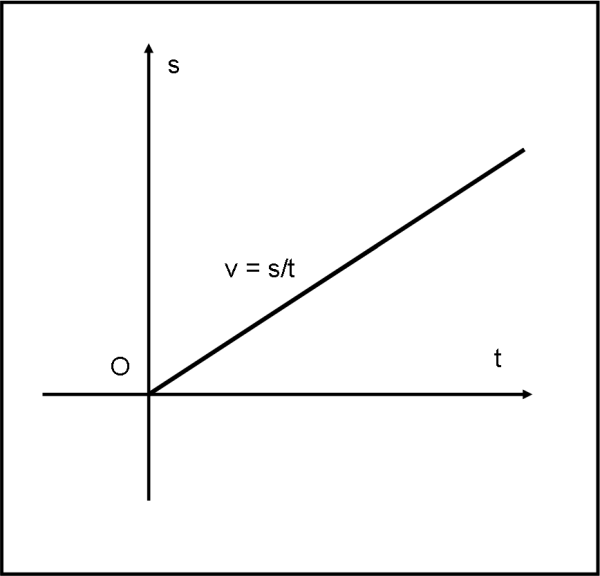
Non potete certo meravigliarvi se il moto del corpo descrive una retta, essendo un risultato che conosciamo ormai come le nostre tasche. In questo tipo di diagramma, la retta rappresenta proprio lo spazio percorso al passare del tempo. Abbiamo una retta per il semplice fatto che la velocità è costante ed è descrivibile con la pendenza della retta, ossia con il coefficiente angolare, ossia –ancora- con la derivata prima dello spazio rispetto al tempo. Essendo, però, questa velocità costante possiamo anche scrivere che la derivata non è altro che il rapporto tra qualsiasi s e il t corrispondente e, quindi:

s/t = v₀

e, ovviamente:

s = v₀t

Leggiamo questa formuletta in modo elementare:

lo spazio percorso dal corpo è uguale al prodotto tra la velocità (costante) e il tempo trascorso.

Guarda caso è una definizione che ci ricorda estremamente bene l’area di un rettangolo: lato per lato, che in questo caso diventa tempo per velocità. Lascio a voi fare l’ultimo passetto di un’ovvietà spaventosa, che confermo immediatamente:

lo spazio percorso da un oggetto in moto rettilineo uniforme è dato dall’area del rettangolo che si ottiene utilizzando la Fig. 2. In parole più costruttive, per conoscere lo spazio percorso da un corpo che si muove con velocità v₀, basta calcolare l’area del rettangolo di lati il tempo trascorso e la velocità costante.

Sembrerebbe una sciocca e inutile conclusione, ma, in pratica ci dice che se conosciamo la velocità è possibile fare il contrario di quello che si fa normalmente in cinematica, quando  si conosce lo spazio percorso nell’unità di tempo e si calcola le velocità. Adesso, invece, partendo dalla velocità ricaviamo lo spazio percorso.

Andiamo avanti con la cinematica elementare e immaginiamo di avere un moto uniformemente accelerato. Cosa vuol dire? Presto detto: la velocità varia in modo uniforme mentre l’accelerazione è costante.

Divertiamoci ancora un poco con i nostri grafici elementari e costruiamo la Fig. 4. Accidenti… ma è sempre la stessa. In realtà no, dato che al posto della velocità c’è adesso l’accelerazione in funzione del tempo. L’accelerazione è però una costante e possiamo calcolare facilmente l’area del rettangolo grigio. Essa è data da at.

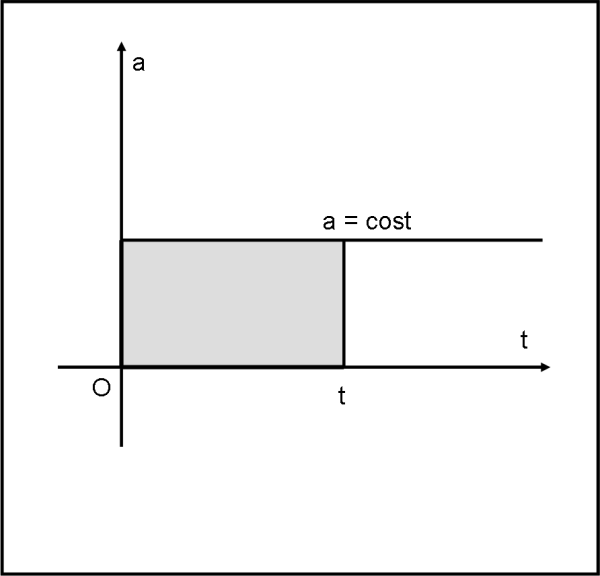
Ma sappiamo molto bene cosa vale at quando a è una costante:

v = at

Come potevamo facilmente dedurre subito, l’area del rettangolo che ha come lati l’accelerazione e il tempo ci regala la velocità.

Possiamo quindi facilmente passare da accelerazione a velocità calcolando l’area del rettangolo, analogamente a quanto abbiamo fatto per velocità e spazio nel caso di moto uniforme.

Il giochino è veramente divertente e vediamo se, anche in questo caso, è possibile arrivare fino allo spazio percorso. Non ci resta che disegnare in Fig. 5 la velocità in funzione del tempo.

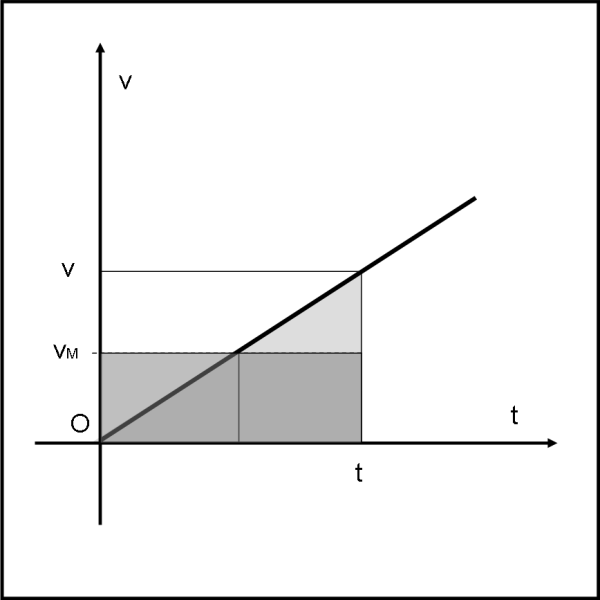
Questa volta non si ottiene certo un rettangolo, ma un triangolo (abbiamo posto v₀ = 0, ossia l’oggetto parte da fermo). Sarebbe molto bello che l’area del triangolo fosse proprio lo spazio percorso… Beh… è proprio così! Basta fare un piccolo ragionamento.

La velocità, rispetto al tempo, descrive una retta. Si può allora considerare senza problemi una velocità media, data proprio da v_M = v/2. Lo spazio percorso nel tempo t con velocità variabile linearmente è uguale allo spazio percorso con una velocità costante uguale a v_M. In parole povere, tutto ciò che abbiamo guadagnato prima di t/2 lo perdiamo dopo t/2 e il risultato è lo stesso. Lo spazio percorso nel tempo t è dato allora da

s = 1/2 vt

Ripetiamo che non abbiamo fatto altro che trasformare un moto uniformemente accelerato in un moto uniforme con velocità uguale al valor medio tra le velocità iniziale e finale. Possiamo allora trasformare il nostro triangolo in un rettangolo che ha un lato uguale a t e un’altezza uguale a v/2.

Ma la sua area è proprio vt/2, ossia esattamente l’area del triangolo di partenza. Abbiamo dimostrato facilmente che anche nel caso di un moto uniformemente accelerato l’area compresa tra la traiettoria della velocità e l’asse delle x è proprio lo spazio s dato da:

s = 1/2 vt       …. (3)

Il nostro moto è però uniformemente accelerato e dobbiamo far comparire l’accelerazione…

Possiamo “recuperare” quanto trovato nella Fig. 4, ossia:

v = at

Sostituendola nella (3) si ha:

s = 1/2 at²       …. (4)

Che è proprio la legge oraria di un corpo che si muove di moto uniformemente accelerato.

Nel caso che non si partisse dall’origine, ma da un punto di ascissa s = s₀ con una velocità iniziale v₀ (caso più generale possibile), l’equazione precedente diventerebbe la ben nota:

s = s₀ + v₀t + ½ at²    …. (5)

Per esercizio, potete anche provare a calcolare la (5) quando, ad esempio, la velocità iniziale non è zero, ma è v₀.  La Fig. 5 diventa la Fig. 6. Nessun problema, basta calcolare l’area del trapezio grigio.

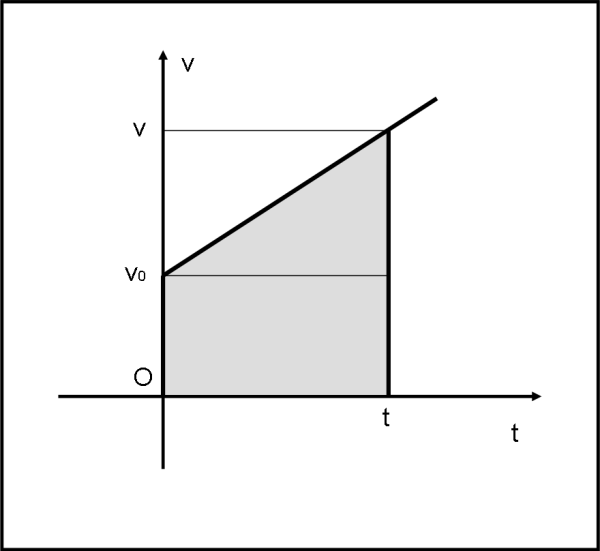
Essa vale

(v₀ + v)t/2 = v₀t/2 + vt/2

Ossia, lo spazio percorso vale:

s = v₀t/2 + vt/2         …. (6)

L’accelerazione, ovviamente, non è più v/t ma (v – v₀)/t (costante)

Per cui

at = (v – v₀)

E ancora:

v = v₀ + at

Sostituendola nella (6)

s = v₀t/2 + v₀t/2+ at²/2  = v₀t + at²/2

Insomma, calcolando le aree più comuni (rettangolo, triangolo e trapezio) siamo riusciti a passare dall’accelerazione alla legge oraria, ossia all’equazione che lega lo spazio al tempo. Veramente banale… quasi ridicolo!

No, non è assolutamente un concetto ridicolo, anche se lo sembra.

Immaginate per un attimo di passare a moti ben più complicati, come quello di un oggetto in orbita attorno al Sole su un orbita ellittica. Cosa possiamo realmente determinare con le osservazioni? Beh, la posizione apparente, la velocità e l’accelerazione, mentre si vorrebbe conoscere la traiettoria realmente descritta. Si esegue quindi proprio la parte finale del nostro discorso. Si usano velocità e accelerazione per arrivare alla legge oraria.

Possiamo anche vedere la faccenda in altro modo, ancora più “fisico”. La legge di Newton parla di forza e di massa. Ma la forza è proprio una massa moltiplicata per un’accelerazione. Si è quindi obbligati a partire dall’accelerazione per passare poi alla velocità e infine alla traiettoria. La realtà della meccanica celeste segue normalmente questo processo logico e matematico.

Non si usano certamente aree di poligoni semplici ed è utile introdurre un operatore che permetta di svolgere il compito delle aree.  In poche parole, calcolare aree sempre più complicate è il primo passo che dobbiamo imparare.

Pensiamo, inoltre, che questa operazione che fa passare da derivate seconde a derivate prime e poi allo spazio è proprio il contrario di quanto siamo ormai capaci di fare: derivando lo spazio rispetto al tempo sappiamo calcolare la velocità, la cui derivata è l’accelerazione.

Da un lato abbiamo un problema di calcolo di aree, dall’altro un problema che sembra proprio l’operazione inversa della derivata. Due modi per ottenere lo stesso risultato. Due modi che corrispondono proprio ai due tipi di integrali, definiti e indefiniti.

Aree e operatori matematici: lo studio degli integrali sta tutto qui. Tuttavia, anticipiamo che, mentre il primo approccio è facilmente descrivibile con la geometria, ma non è assolutamente indicato per ottenere un risultato numerico, il secondo si basa solo su un processo matematico che permette il calcolo vero e proprio. L’ideale sarebbe usare il secondo per ottenere il primo, ossia trovare una relazione ben definita che leghi i due tipi di approccio. A questo ci pensa il teorema fondamentale del calcolo integrale, una scoperta fantastica che non potremo certo trascurare.

Sì, siamo andati un po’ troppo avanti, ma lo abbiamo fatto solo per illustrare la problematica nel suo insieme e cominciare a capire il perché di certi approcci che sembrano estremamente distanti tra loro. Dimenticate (per adesso) quanto ho detto nella parte finale e torniamo alle aree, affrontandole in modo generale.

Forse vi sembrerà che abbia messo troppa carne al fuoco? Potevo seguire uno schema più rigido, come viene fatto normalmente. Tuttavia, la scelta è dipesa dal fatto che volevo approfittarne per richiamare la legge oraria, il significato geometrico della derivata e introdurre il concetto più generale dell’area… Come al solito, cerchiamo i concetti prima delle regole, che rischiano di diventare troppo presto monotone e, quindi, pressoché inutili.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica