E' venuto l'ora tanto attesa, preparata con tutte le precauzioni del caso. Dopo il triangolo, dove la funzione è una retta inclinata, non abbiamo più problemi a passare a una funzione qualsiasi. Il gioco lo conosciamo bene e ci porta automaticamente alla definizione di integrale definito. Ci fermiamo un poco, prima di proseguire, dato che quasi senza accorgercene abbiamo introdotto il "celebre" integrale di una funzione ed è giusto "digerirlo" molto bene

Bando alle ciance e consideriamo una funzione qualsiasi y = f(x). Siamo interessati a calcolare l’area contenuta tra la funzione e l’asse delle x in un certo intervallo (a,b), come rappresentato nella Fig. 1.

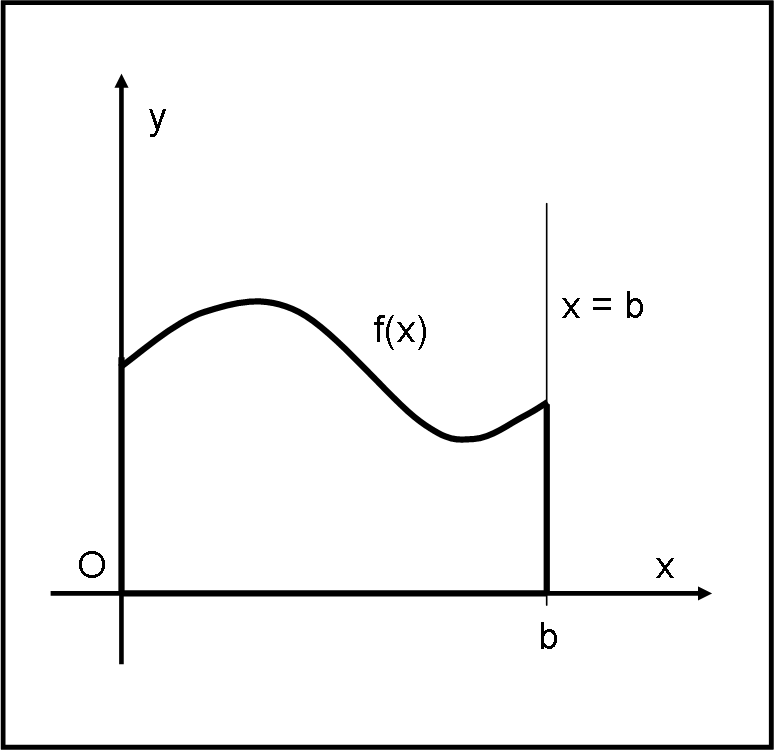
Non vi è certo sfuggito che questa figura potrebbe essere considerata come la rappresentazione di un moto comunque accelerato, inserendo la v al posto della y e il tempo al posto della x. L’area racchiusa ci darebbe la legge oraria come già dimostrato nel capitolo 40.

Tuttavia, a questo punto, l’area da calcolare non è certo compresa tra quelle ben note. Ecco che i nostri rettangolini variabili ci vengono estremamente utili, come negli approcci di Archimede.

L’area che vogliamo calcolare è sempre quella limitata tra la funzione (in questo caso NON costante e nemmeno rettilinea), l’asse delle x, e le rette x = 0 e x = b. Stiamo parlando di aree di figure con un lato curvilineo e quindi sempre finite e con un certo valore ben prefissato.

Ricordando in qualche modo Archimede e avendo a disposizione solo l’area del rettangolo, non ci rimane che cercare di approssimare quest'area con una serie di rettangolini tutti interni (Fig. 2) che abbiano larghezza costante dx. L’altezza dei rettangolini è, invece, il valore minimo assunto da f(x) nell’intervallino definito da dx, ossia f_m(x).

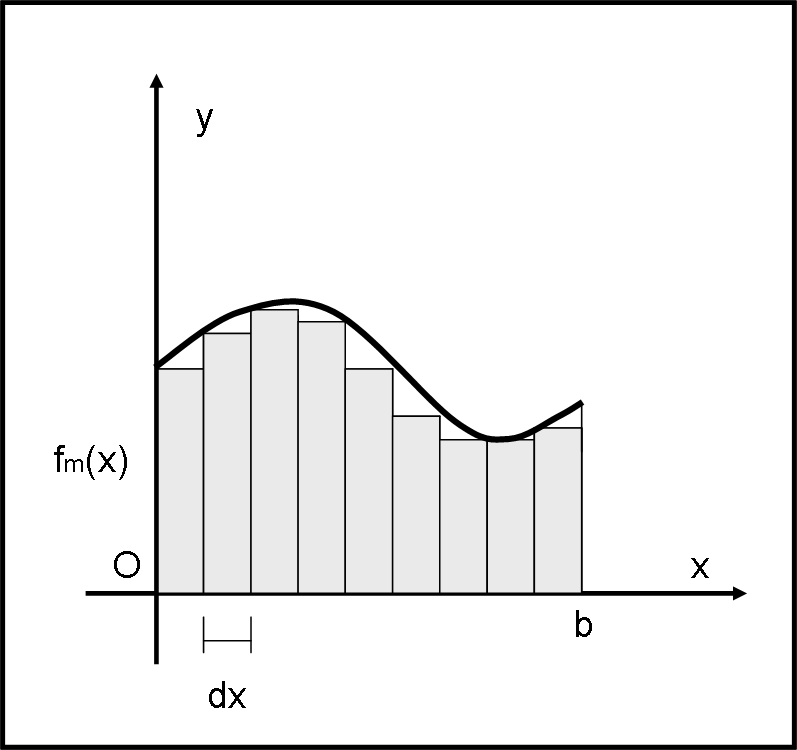
I rettangolini sono in numero di n e la loro area è data da

A_mk = f_mk(x) dx_k

Dove k indica il rettangolino k-esimo, con k che arriva fino a n. dx è sempre lo stesso, ma abbiamo inserito il pedice k per sapere quale sia veramente allo scorrere di x lungo il segmento O-b, dato che cambia continuamente l’altezza del rettangolino. Analogamente, abbiamo aggiunto una k anche nella f_m

Ovviamente, questa volta i rettangoli sono sempre diversi tra loro e non più “ripetitivi” come quelli del caso “stupido” del rettangolo precedente. Assomiglia molto all'approccio che abbiamo usato per il triangolo. L'unica vera differenza è che in quel caso la y =f (x) era sempre uguale a x, mentre adesso vale f(x) complicata quanto si vuole (l'importante è che sia continua).

Non ci resta che sommare tutti i rettangolini ottenuti, ossia tutte le aree A_mk

A_m =  Σⁿ_{k = 1} f_mk(x) dx_k

Non è certo l’area A della strana figura curvilinea, ma siamo sicuri che:

A_m < A

Non abbiamo ottenuto una grande approssimazione, ma per lo meno abbiamo imitato Archimede. Per continuare a imitarlo, basta restringere l’intervallino dx e aumentare il numero n di rettangolini. La Fig. 3 ci mostra il netto miglioramento.

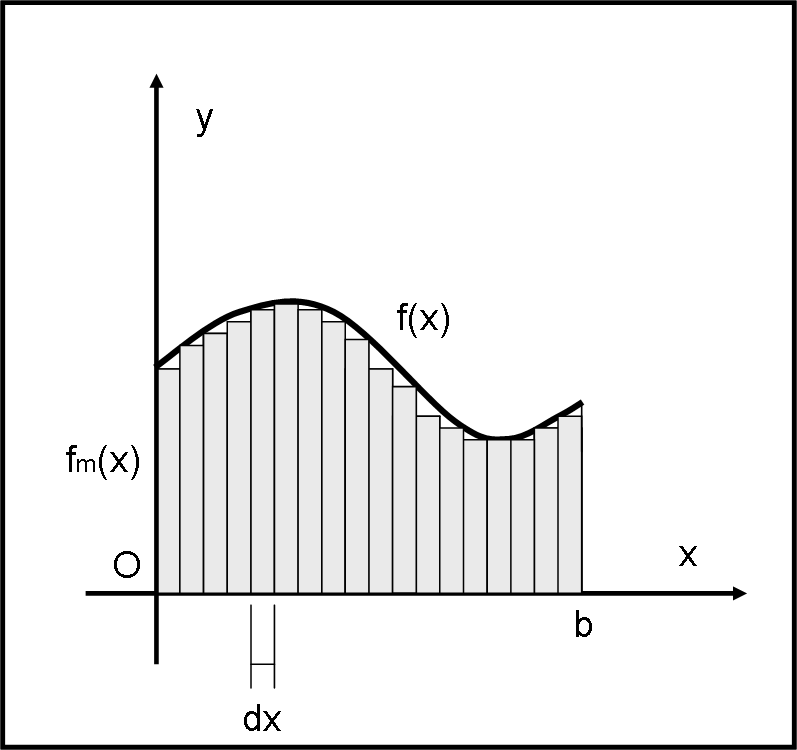
Prima di proseguire in questo gioco iterativo, cerchiamo di prendere la funzione tra due fuochi. Sempre considerando gli stessi intervallini dx, scegliamo, in Fig. 4, come loro altezza il valore massimo della funzione f(x) in ciascuno intervallino e la chiamiamo f_Mk(x).

Calcoliamone l’area

A_M,k = f_Mk(x) dx_k

Sommandole tutte (anch’esse sono n aree), si ha:

A_M =  Σⁿ_{k = 1} f_Mk(x) dx_k

In questo secondo caso siamo sicuri che:

A < A_M

Riassumendo:

A_m < A < A_M

E, per esteso:

Σⁿ_{k = 1} f_mk(x) dx_k < A <  Σⁿ_{k = 1} f_Mk(x) dx_k

Se la funzione è continua, si deduce facilmente che, al crescere del numero di intervallini dx (sempre più piccoli), l’area esterna e quella interna si avvicinano sempre più all’area effettiva definita dalla funzione f(x).

Possiamo, perciò, passare al limite delle due somme. Essi devono convergere entrambi verso l’area effettiva.

lim_n→∞Σⁿ_{k = 1} f_mk(x) dx_k = A =  lim_n→∞Σⁿ_{k = 1} f_Mk(x) dx_k

L’operazione che abbiamo fatto, sia provenendo dall’interno che dall’esterno, ci ha portato al valore esatto dell’area definita dalla funzione f(x). Abbiamo eseguito delle somme facendo tendere a infinito il numero di intervallini considerati, compresi tra il valore iniziale e quello finale della x (O e b). Ovviamente, al crescere di n decresce la lunghezza dell’intervallo dx. Se dx tende a zero, la f_m e la f_M tendono allo stesso valore f.

Definiamo integrale definito della funzione f(x) nell’intervallo da O a b, l’area definita dalla funzione f(x) e lo scriviamo:

A = ∫_o^b f(x)dx

Esso altro non è che lim_n→∞Σⁿ_{k = 1} f_mk(x) dx_k  o, analogamente, lim_n→∞Σⁿ_{k = 1} f_Mk(x) dx_k.

Il segno di integrale rappresenta una S allungata, proprio per ricordare che non è altro che una sommatoria, capace di regalarci l’area relativa a una funzione qualsiasi.

Se, invece dell’origine, si parte da una qualsiasi ascissa a si ha:

A = ∫_a^b f(x)dx

Riuscire a calcolare quest'area vuole dire risolvere enormi problemi della fisica dato che, ad esempio, ci fa passare da accelerazione a velocità e da velocità a spazio percorso, per moti qualsiasi. Ma anche il lavoro compiuto da una forza e tante altre cose...

Il vero problema è che NON è assolutamente facile calcolare il limite di una sommatoria e che occorre trovare un sistema puramente analitico . Il sistema esiste e si basa sul fondamentale teorema di Torricelli-Barrow, che cercheremo anche di dimostrare. Per adesso, però, godiamoci un poco l’integrale definito, capace “teoricamente” di calcolare tutte le aree che vogliamo, anche quelle negative, quelle comprese tra due funzioni e tanto altro ancora. E’ quindi essenziale stabilire alcune loro proprietà.

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica