Questo articoletto riprende il quiz sulle comete di Kreutz proposto qualche giorno fa e a cui è già stata data una risposta molto semplificata. Vediamo di studiare un po’ meglio il moto del Sole all’interno del suo sistema (senza considerare quello ben più ampio e complesso all’interno della Via Lattea e di questa all’interno del suo ammasso locale). La precisazione appare importante, quando si legge spesso e volentieri che il baricentro del sistema Solare è sempre all’interno del Sole. No, non è affatto vero e le comete di Kreutz, che hanno un perielio piccolissimo, ne danno una prova tangibile (se mai ce ne fosse bisogno).

Normalmente si usano due concetti che devono comunque coincidere: (1) la traiettoria di un pianeta è un’ellisse di cui il Sole occupa uno dei fuochi; (2) un sistema doppio (stellare o planetario) è composto da due astri che rivolvono attorno al comune baricentro.

Beh… la legge che governa questi due concetti è sempre e soltanto la legge di gravitazione universale di Newton o -se preferite- la deformazione spazio temporale imposta dalla relatività generale di Einstein. Resta, comunque, il fatto che i due modi di dire devono essere la stessa cosa.

A volte, si tratta solo di cambiare sistema di riferimento e considerare il moto di un oggetto intorno all’altro. O, addirittura, considerare fermo il sistema e studiare il campo gravitazionale rotante  che porta alla definizione dei punti lagrangiani e cose del genere.

In questo caso, però, noi vogliamo restare molto più terra-terra e riferirci al centro più logico dell’intero Sistema Solare. Sabbiamo bene, dalla meccanica classica, che, dato un sistema di n punti massicci esiste un punto molto particolare in cui si può concentrare tutta la massa. Tale punto risulta fermo o al più in moto rettilineo uniforme (come dice Galileo). Questo punto è il baricentro (o il centro di massa) del sistema considerato chiuso, ossia non influenzato da forze esterne.

Si potrebbe anche parlare di momento angolare  e di quantità di moto, ma questa volta non vogliamo scendere in troppi particolari e ci limitiamo a dire quanto segue: “I pianeti, i corpi minori, il Sole stesso, rivolvono tutti attorno al loro comune baricentro”. Già questa frase  conferma chiaramente che le traiettorie dei corpi planetari devono fare riferimento al baricentro e non al Sole.

Nel caso che il sistema sia composto da due soli corpi, l’equazione del moto può essere risolta perfettamente (attraverso gli integrali, come già accennato) e si arriva alla ben nota conclusione: “Due corpi rivolvono attorno al comune baricentro”. Il fatto che  uno dei due occupi un certo punto detto fuoco non è assolutamente vero o, almeno, potrebbe essere solo una rappresentazione particolare  utilizzata per descrivere la situazione.

Tuttavia, vivendo su un piccolo pianeta e studiando il moto di oggetti ancora più piccoli come asteroidi e comete, la massa di uno dei due corpi è decisamente molto inferiore a quella dell’altro (il Sole). In questo caso, si può facilmente approssimare la situazione dicendo che il più piccolo descrive una traiettoria ellittica di cui l’altro, più massiccio, occupa uno dei fuochi (con gran piacere di Keplero). In poche parole, si considera trascurabile la massa dell’oggetto minore.

E’ questo che, di solito, si fa in meccanica celeste quando si studiano le orbite “kepleriane” degli asteroidi attorno al Sole. Tuttavia, questa è una approssimazione che, molto spesso, non può essere accettata. Il moto di un asteroide è influenzato pesantemente dalla presenza degli altri pianeti e ne segue che l’orbita finale è tutt’altro che una traiettoria chiusa, ma varia continuamente.

Basta un solo pianeta di massa considerevole per rendere il problema analiticamente irrisolvibile. Per trovare una soluzione è necessario eseguire approssimazioni di vario tipo e adottare le integrazioni numeriche di cui abbiamo già parlato.

Immaginiamo facilmente il caos che ne deriva quando il numero dei corpi planetari cresce di numero e la precisione richiesta è sempre più restrittiva. La meccanica celeste ha di che divertirsi. Abbiamo parlato di asteroidi, ma potevamo parlare di comete o di pianeti, ovviamente.

Tuttavia, resta indubbio un fatto: i corpi planetari, qualsiasi essi siano, rivolvono attorno al comune centro di gravità. A questo fatto va, però, aggiunto il problema delle perturbazioni reciproche (passaggi ravvicinati a pianeti, risonanze di moto medio, ecc.). Possiamo, però, per il momento, limitarci al concetto di base, che ripetiamo ancora: i corpi del sistema solare rivolvono attorno al baricentro del Sistema solare e non intorno al Sole. Ne segue che anche il Sole è costretto a muoversi continuamente!

Stiamo tagliando un capello in due? Molto spesso sì, ma non per oggetti che si avvicinino molto al Sole… come le comete di Kreutz.

Per renderci conto di questo fatto, seguiamo una strategia che  regala delle figure molto belle e che  fa “pesare” molto bene il ruolo dei pianeti maggiori e minori sulla posizione del baricentro dell’intero Sistema Solare.

Cosa stiamo per fare? Poniamo l’origine dei nostri assi nel baricentro del sistema che deve essere sempre fisso e vediamo come si muove il Sole attorno ad esso. Per semplificare la trattazione, si potrebbe anche considerare il Sole come fisso e vedere come si muove il baricentro. Avremmo eseguito una pura e semplice trasformazione di coordinate. Purtroppo, a volte, questa visione alternativa (che non cambia il fenomeno fisico) crea non pochi problemi. Si legge, infatti, che il moto dei pianeti fa variare costantemente il baricentro del Sistema Solare. No, non è assolutamente vero, per la stessa definizione di baricentro! Ripetiamo: è il Sole che ondeggia e non il baricentro.

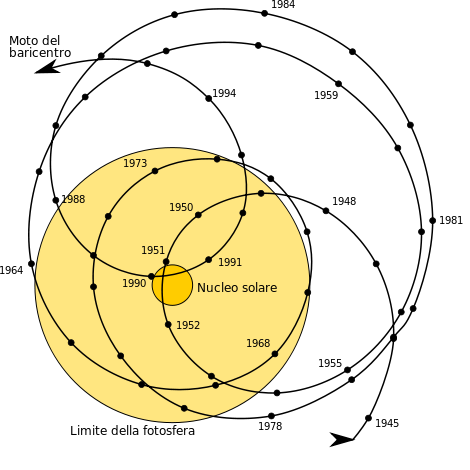
La Fig.1 mostra il movimento “fittizio” del baricentro rispetto al Sole considerato fermo. Ma la figura sarebbe del tutto simile, eliminando il cerchio del Sole e considerando il baricentro come punto fisso centrale e la curva quella descritta dal centro del Sole. E’ solo una questione di sistema di riferimento e non certo un problema concettuale.

In un primo tempo, volevo mostrare varie figure che illustrassero il contributo al movimento del Sole dei vari pianeti.  Poi, ho recuperato un bellissimo programmino “pappa pronta”. Magnifico! Dato che sappiamo ormai benissimo come si può ottenere e sapendo che carta e matita ci farebbero sprecare anni di calcoli, non vi è niente di male a usare la memoria e la velocità del nostro “stupido” computer, dicendo grazie a chi ha scritto il programma relativo (di alta meccanica celeste). Sapendo che non è un processo misterioso (che è meglio nascondere ai comuni mortali) quello che permette di eseguire una simulazione, la si può utilizzare senza alcun problema… anzi, ben venga!

Cosa fa il simulatore? In modo semplicissimo permette di inserire i pianeti uno alla volta o a gruppi e vedere come cambia il moto del Sole. Ovviamente, introducendo più pianeti si deve tener conto delle perturbazioni mutue tra di loro. Insomma, un lavoraccio… ma il divertimento è assicurato.

QUI trovate la simulazione.

Non aspettatevi figure simmetriche, anche se a prima vista lo sembrano. I moti dei pianeti seguono ellissi (non circonferenze) e non vi sono risonanze perfette che li leghino tra loro.

Noterete subito che  Giove e Saturno riescono a portare l’intero Sole al di fuori del baricentro. Non molto, ovviamente, ma quel tanto che basta, a volte, perché una cometa che si spinga a distanze piccolissime dal baricentro possa cadere al suo interno o sfiorarla a una distanza di quasi-sicurezza.

Dobbiamo fare una precisazione doverosa. In modo molto semplicistico si potrebbe dire che il cosiddetto “perielio” dell’orbita cometaria sia, in realtà, un “peribaricentro” o qualcosa del genere. In tal modo, il discorso fatto precedentemente sarebbe completamente valido. In realtà, però, mentre la cometa si avvicina al Sole il sistema, indipendentemente dal moto del Sole, si riduce a due corpi: Sole e cometa. Dato che la massa della cometa è trascurabile, potremmo, quindi, dire che la cometa cerca di mantenere il Sole in uno dei fuochi della sua orbita e lo segue nel suo moto attorno al baricentro. E’ un po’ come se la cometa volesse a tutti i costi finire arrostita!

Un moto non certo facile da descrivere e che non è uguale a quello di due corpi isolati, di cui uno con massa trascurabile. Ne segue che, anche nella realtà dei fatti, alcune comete riescono a passare indenni durante il passaggio al perielio. In pratica, la cometa deve dire grazie alla posizione relativa di Giove e Saturno: se sono dalla stessa parte si può salvare (baricentro e Sole sono distanti tra loro); se sono da parti opposte, centro del Sole e baricentro coincidono quasi completamente e per la cometa non ci sono speranze.

Teniamo anche conto che nel calcolo del baricentro conta sì la massa dei corpi in gioco, ma anche la distanza. E’ il concetto dell’altalena: si può controbilanciare un amico molto pesante allontanandosi dal fulcro. Ne segue che Saturno gioca quasi come Giove, malgrado sia più piccolo e che Nettuno ha un ruolo più importante di Urano, dato che a parità di massa si trova … al bordo dell’altalena!

Comunque, giriamola come vogliamo, ma il problema resta solo e soltanto un problema degli n-corpi, in cui sul moto di un corpo di massa trascurabile giocano le perturbazioni di tutti i suoi compagni di viaggio. Questa è la Meccanica Celeste…

 

QUI trovate la domanda del quiz

QUI è spiegato in modo approfondito cos'è il baricentro di un sistema