Discutiamo un poco attorno al calcolo di aree un po’ strane, proprio ciò che rende, tra molte altre cose, gli integrali uno strumento insostituibile. Non siamo ancora in grado di CALCOLARE realmente gli integrali (e quindi le aree), ma possiamo iniziare a divertirci, preparandoci allo scopo, dividendo, sommando e sottraendo aree parziali e anche … negative.

Cominciamo con un piccolo paradosso. Consideriamo, ad esempio, la Fig. 1 dove è rappresentata la funzione sen (x) nell’intervallo tra 0 e 360°.

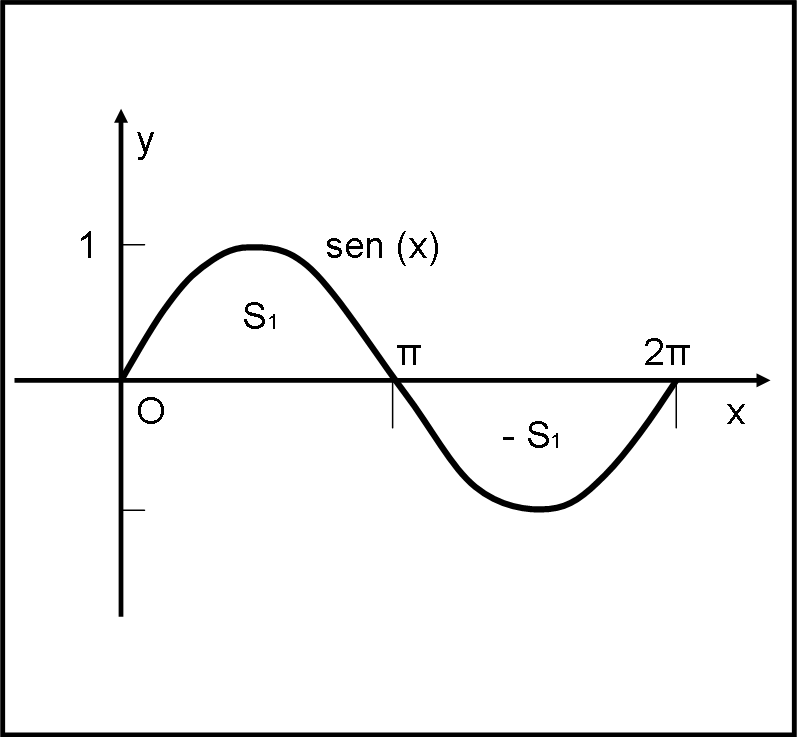
L’esercizio che vogliamo affrontare è quello di calcolare l’area compresa tra la curva e l’asse delle x. Potremmo cominciare a fare i nostri rettangolini tra l’asse x e la funzione. Tuttavia, possiamo cercare si semplificare un po’ l’approccio

Separiamo la funzione in due parti, quella tra 0 e 180° e quella tra 180° e 360°. Sappiamo benissimo che la funzione seno si ripete dopo 180°, cambiando solo il suo segno. Dalle proprietà degli integrali, sappiamo anche che l’integrale di una funzione nell’intervallo (b – a) è uguale alla somma degli integrali tra a e c e tra c e b, con c punto qualsiasi tra a e b. In altre parole, per avere l’area totale, posso calcolare separatamente le due aree e poi sommarle.

Sarebbe anche facile ottenere il valore numerico dell’area della funzione seno tra la curva e l’asse x, ma non abbiamo ancora l’operatore necessario, e quindi accontentiamoci di chiamarla S1. Ricordiamo, però, che essa si trova approssimando la funzione con rettangolini infinitesimi sia da sotto che da sopra. Ogni rettangolino ha lato orizzontale dx (che essendo un intervallo è sempre positivo anche se si riferisce a x negative) e come lato verticale una certa y che è sia la massima che la minima, in quell’intervallimo

Passando al limite otteniamo proprio l’area “curvilinea”. Sono cose che ormai sappiamo molto bene… Ciò di cui siamo sicuri è che il lato verticale dei rettangolini , sia che sia il minimo o il massimo della funzione, deve, comunque, essere sempre positivo.  Le aree sono espresse dal prodotto tra dx (sempre positivo) e una y (che in questo caso è positiva) e il risultato deve essere positivo. La somma di tanti rettangolini positivi dà un numero positivo S₁, che non è altro che l’integrale di questa prima parte della funzione. E fin qui niente di male…

Ripetiamo lo stesso procedimento tra 180° e 360°. Non cambia assolutamente niente, data la simmetria della funzione seno, tranne una cosa molto importante: il segno dei lati verticali dei vari rettangolini sono, adesso, tutti negativi. I lati dx sono invece sempre positivi e, alla fine, troviamo un numero (ossia l’integrale della seconda parte) che è costretto a essere negativo, anche se è uguale in valore assoluto a S1.

Non ci resta che sommare i due integrali per avere l’area totale S. Ovviamente, otteniamo un risultato che non può certo soddisfarci:

S = S₁ + (- S₁) = 0

No, non possiamo certo credere che l’area totale sia uguale a zero, lo vediamo chiaramente dalla figura. Forse gli integrali non funzionano così bene per calcolare le aree? Assolutamente no, è solo questione di intendersi. L’integrale calcola esattamente l’area racchiusa tra una funzione e l’asse delle x, ma è costretto a portarsi dietro un segno che le aree non possono avere (le aree sono sempre positive). Non ci resta, allora, che fare una cosa semplicissima: ogni volta che abbiamo a che fare con una curva posta al di sotto dell’asse delle x, ci dobbiamo ricordare di cambiare il segno all’integrale e tutto torna perfettamente.

Applichiamolo al caso in esame

S = S₁ + S₁ = 2S₁

Perfetto, adesso sì che ci siamo!

Ancora una volta non ridete di queste trattazioni così elementari e apparentemente ovvie. Vedremo in seguito, quando saremo capaci di calcolare veramente gli integrali, che avremmo trovato un risultato davvero assurdo se non ci fossimo premuniti di dividere la funzione in due intervalli e avessimo calcolato il suo integrale direttamente tra 0 e 360°. Come è facile immaginare avremmo trovato un risultato uguale a zero e, se non ci avessimo ragionato sopra, avremmo considerato l’integrale del seno, tra 0 e 360°, uguale a zero. Un risultato completamente sbagliato!

Non ditemi: “Ci saremmo subito accorti di quello che stavamo facendo e saremmo corsi ai ripari, come abbiamo fatto precedentemente”. In un caso così semplice avreste sicuramente ragione, ma non sempre la funzione da integrare è così immediata da “vedere” e il calcolo dell’integrale porterebbe a risultati sbagliati che faremmo fatica a riconoscere come tali. Inoltre, non sempre si usano gli integrali per calcolare aree “canoniche”, dato che spesso si può essere interessati a somme algebriche, ossia con segno.

In ogni modo, per adesso, impariamo che è sempre utile e fondamentale sapere dividere la nostra funzione in intervalli in cui essa sia sempre negativa o sempre positiva, in modo da potere poi cambiare oppure no il segno dell’integrale trovato.

Questo caso particolare e le sue conseguenze ci insegnano come agire quando ci viene chiesto il calcolo di aree comprese tra due curve qualsiasi (che si intersecano tra loro). La strategia da seguire è innanzitutto quella di trovare i limiti estremi dell’intervallo dell’area da calcolare, ossia i punti di intersezione tra le due funzioni. Fatto questo, bisogna stare bene attenti a suddividere l’area in zone tali che le aree corrispondenti siano completamente o sopra o sotto l’asse delle x. Alla fine si può utilizzare la proprietà richiamata all’inizio ed effettuare la somma di tutti gli integrali, cambiandogli di segno quando si riferiscono a zone al di sotto dell’asse delle x.

Vediamo qualche esempio indicativo, che ci servirà a richiamare anche la soluzione dei sistemi di due equazioni in due incognite.

L’esercizio è : calcolare l’area tra due parabole di equazione

y = 2x²                   

y = 3 – x²

L’area da calcolare è la S colorata in azzurro in Fig. 2.

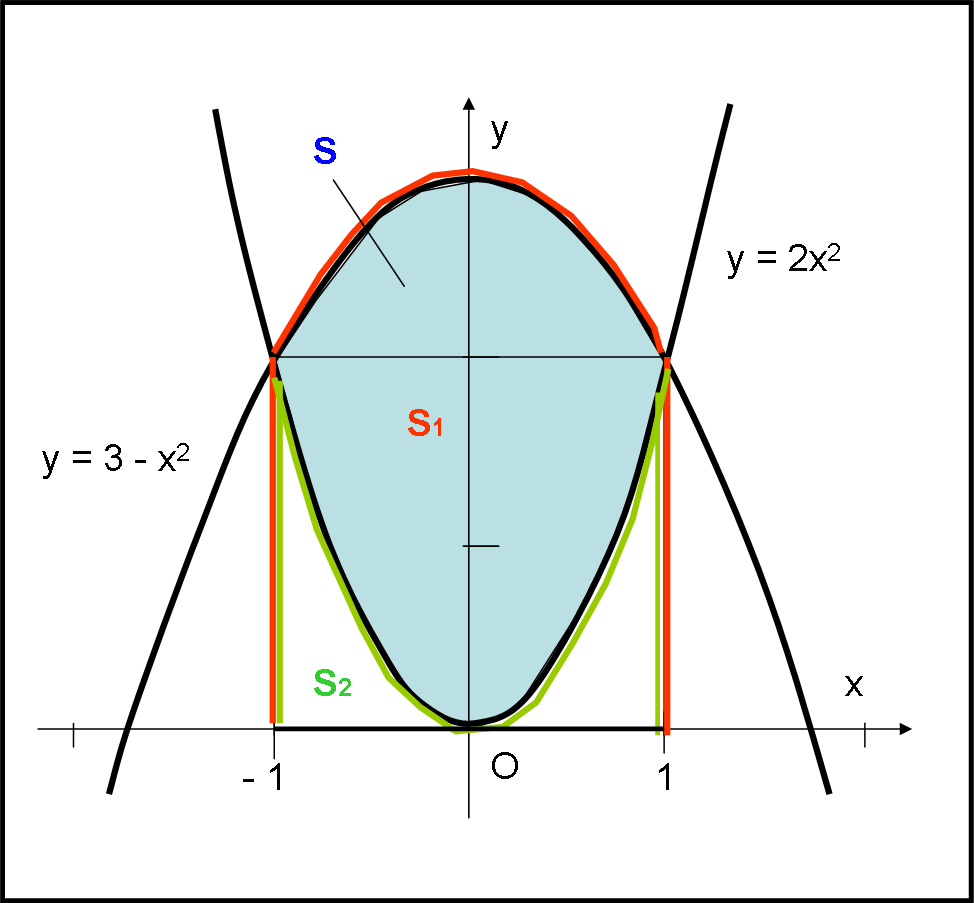
Iniziamo col trovare i limiti dell’integrale, ossia il punto più a sinistra e quello più a destra dell’area in questione.

Essi sono gli unici punti appartenenti ad entrambe le curve e quindi devono soddisfare entrambe le equazioni precedenti.

Basta, perciò, uguagliare la prima con la seconda (ciò vuol dire uguagliare la y) e si ha subito:

2x² = 3 – x²

Ossia:

3x² = 3

x² = 1

Le due soluzioni sono

x₁ = -1

x₂ = 1

Esse diventano anche gli estremi dell’intervallo in cui è compresa l’area. Essa risulta tutta POSITIVA e quindi si può calcolare giocando un po’ con gi integrali delle due funzioni. Prima si calcola quello relativo alla parabola con il vertice in alto e si ottiene tutta l’area delimitata dalla linea blu (S₁). A questa togliamo l’integrale relativo alla seconda parabola (S₂), quella con vertice nell’origine, (delimitata dalla linea rosa). La differenza tra gli integrali ci regala l’area voluta.

S = S₁ – S₂

Ovviamente la faccenda si complica se spostiamo verso il basso le due parabole (basta aggiungere un termine noto negativo ad entrambe). Troveremmo qualcosa come quello rappresentato nella Fig. 3.

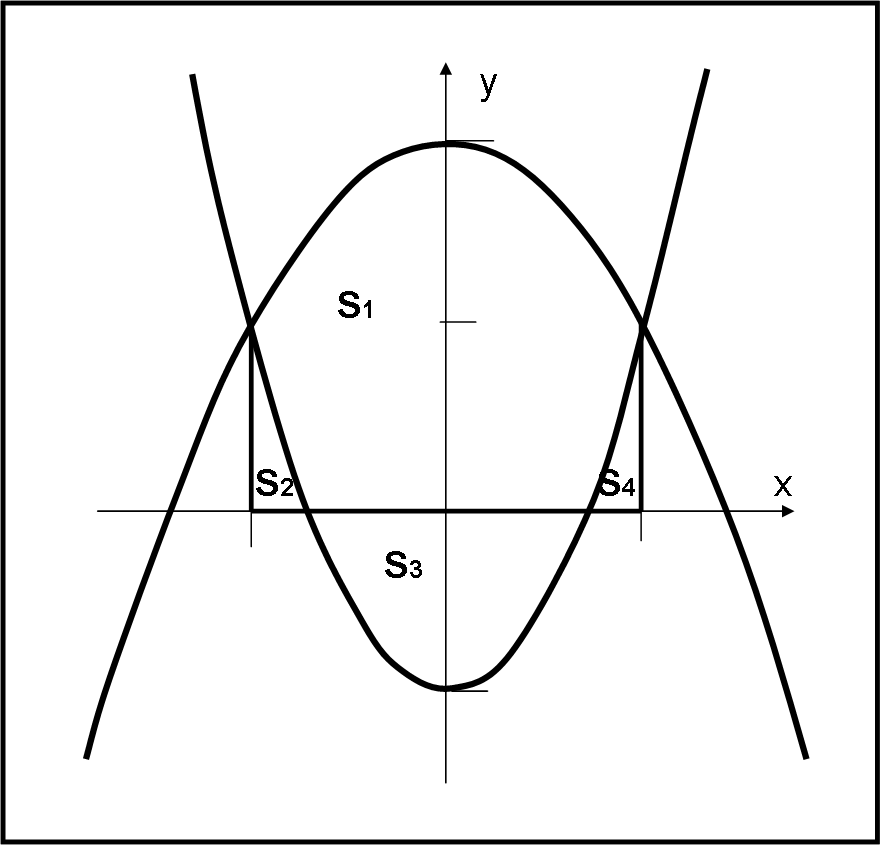
Tutto sembra uguale a prima, ma adesso dobbiamo non solo trovare i limiti dell’intervallo, ma anche i punti relativi alle aree positive e negative. Insomma, il numero di integrali da sommare, con segno cambiato oppure no, aumentano.

In questo caso abbiamo:

S = S₁ – S₂ + S₃ – S₄ = S₁ – 2S₂ + S₃

S₃ si riferisce all’integrale sotto l’asse x che risulta negativo e che quindi deve essere cambiato di segno, mentre S₂ = S₄.

Resta il fatto che le aree finali devono essere uguali e quindi si capisce abbastanza bene che si potrebbe sempre agire sull’asse delle  x e spostarlo verso il basso fino ad avere tutta l’area positiva. Ciò, in parole tecniche, vuol dire effettuare un cambiamento di coordinate (una sola in questo caso).

Si potrebbero inventare situazioni oltremodo complicate e strane. Ve ne propongo, invece, una piuttosto semplice, ma che, utilizzando una proprietà degli integrali (non vi dico quale…), si riduce a un’area veramente facilissima da calcolare numericamente. In questo caso le due curve non si intersecano e si richiede un’area che è delimitata da un certo intervallo delle ascisse.

Consideriamo le due funzioni:

y = x²

y = x² + 1

Esse sono disegnate in Fig. 4.

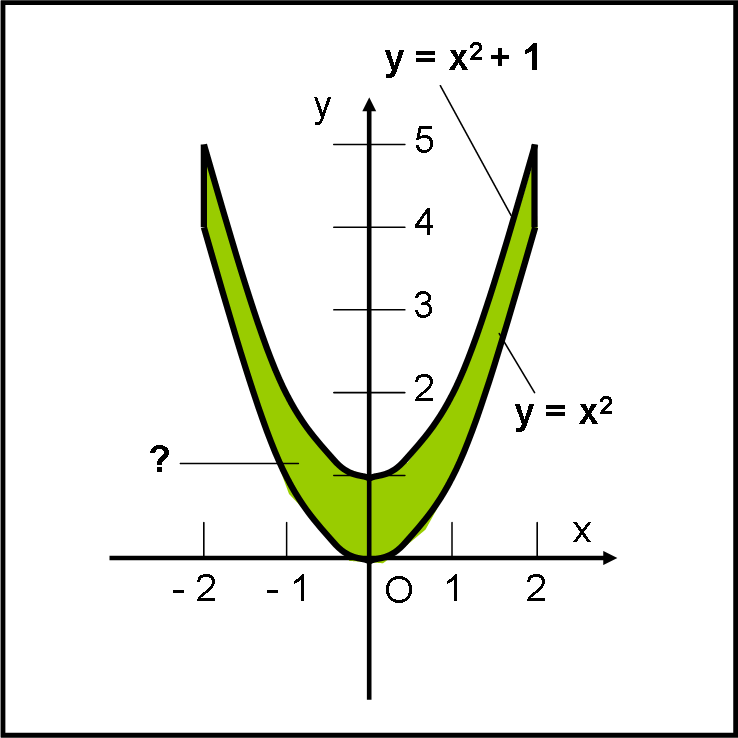
Ditemi subito, senza bisogno di fare figure supplementari o calcoli che abbisognino di carta e matita, quanto vale “numericamente” l’area racchiusa tra le due parabole nell’intervallo compreso tra x = - 2 e x = 2, spiegando come avete fatto (senza saper calcolare, ancora, gli integrali definiti…).

Potremmo complicare di molto le cose e divertirci a incastrare aree, ma rimarremmo sempre legati a simboli e non a valori numerici (a parte il problemino precedente) . E’ proprio necessario imparare a calcolare gli integrali, ossia dare alle aree dei valori numerici. Per far ciò, lasciamo momentaneamente da parte la visione geometrica dell’integrale definito e torniamo alle velocità e accelerazioni che ci avevano già indicato una via diversa da seguire: l’integrale sembra proprio un’operazione matematica che è l’inverso della derivata…

 

QUI il capitolo precedente

QUI il capitolo successivo

QUI l'intero corso di matematica