Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Questa parte non è altro che la risposta al QUIZ e va ancora considerata come una preparazione o -meglio- un allenamento per dedicarsi al vero studio di cosa comporti utilizzare la vecchia definizione in un caso relativistico. Per poterlo fare sarà necessario costruire un esperimento che serva allo scopo e non nasconda la polvere sotto al tappeto.

I solutori del QUIZ mi abbiano pazienza e considerino quanto segue solo come un ulteriore ripasso.

Componiamo le velocità

Prima di iniziare, ribadiamo un paio di concetti che ormai dovrebbero essere ben digeriti. Tuttavia, benché digeriti, è utile, comunque, sintetizzarli per cominciare al meglio il cammino verso la dinamica relativistica. La loro trattazione completa si trova, comunque, QUI e QUI. Sto parlando, ovviamente, della combinazione relativistica delle velocità.

Immaginiamo in Fig. 1, un sistema  S’ (una nave interstellare con il suo capitano) che si muove rispetto a noi  (un papallo S?) alla velocità v diretta secondo l'asse x. All’interno della nave vi è un oggetto P’ che si muove con velocità u' = u’_x nella stessa direzione dell’astronave. Notate l’uso dell’apice.

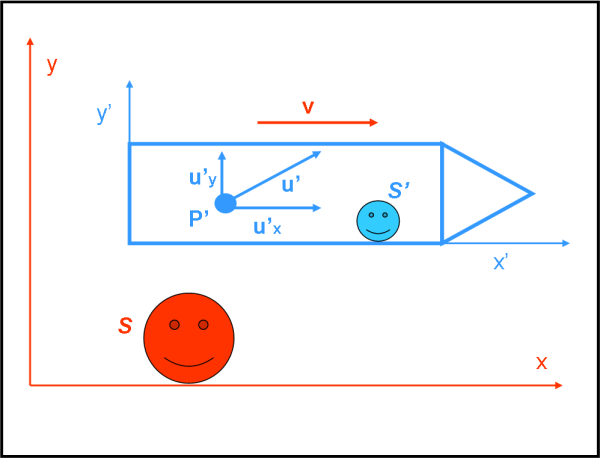
La velocità v è qualcosa di cui ci accorgiamo noi e quindi è senza apice (sistema di S). La velocità u’_x è un qualcosa di cui si accorge il capitano (S’) e quindi deve avere l’apice. Ciò vuole dire che, per il capitano che crede di essere fermo, l’oggetto P’ si muove solo secondo u’_x.  Ci chiediamo: “A quale velocità viene visto viaggiare l’oggetto P’ da noi, papallo S, ossia qual è la sua velocità u_x senza apice (essendo misurata nel sistema S)?” Se rispondesse Galileo ci direbbe:

u_x = v + u’_x.

Se fosse realmente così, però, la somma v + u’_x potrebbe diventare tranquillamente più grande di quella della luce. Ne segue che, in campo relativistico, bisogna evitare che ciò accada. Deve esistere una trasformazione tra chi sta fermo e tra chi si muove, che permetta di non correre questo rischio. E così cadiamo nelle trasformazioni di Lorentz. Applicandole correttamente, si trova che la somma galileiana delle velocità può ancora andar bene fino a che stiamo trattando con velocità molto basse, dopo di che la formula si complica e ci porta a eseguire la somma, tenendo conto di certi fattori di correzione.

u_x = (v + u’_x)/(1 + vu’_x/c²)   …. (1)

Il denominatore è una quantità sicuramente maggiore di uno, da cui segue che la velocità orizzontale finale è sicuramente più piccola della somma delle due velocità. Anche se imponessimo che sia v che u’_x siano uguali alla velocità della luce, otterremmo un valore finale u_x = 2c/(1 + 1) = c. Einstein ci sapeva fare...

Fin qui abbiamo trattato una composizione di velocità che hanno la stessa direzione. Vi dico subito che nel prosieguo dell'articolo questa componente ci interesserà ben poco, ma è sempre meglio averla sott’occhio.

Molto più interessante è il caso in cui la velocità u’ sia diretta in modo qualsiasi (ragioniamo comunque sempre su un piano e quindi con una componente x e una y). Per lavorare con sicurezza e chiarezza è necessario scomporre la velocità u’ nelle sue due componenti: una nella direzione del moto dell’astronave rispetto a noi (u’_x parallela a v, come nel caso precedente) e una in direzione ortogonale (u’_y) .

Per Galileo la velocità vista da S porterebbe a:

u_x = u’_x + v

e

u_y = u_y’

e niente, in fondo, cambierebbe, dato che la componente lungo x è già stata trattata prima, mentre quella ortogonale rimarrebbe immutata. Ne segue che la velocità totale vista da S si ottiene sommando i vettori u_x e u_y = u_y’ (il modulo u si determina attraverso il banale teorema di Pitagora)

Nel caso relativistico le cose si complicano. Diciamolo prima a parole e poi passiamo alle formule.

La componente u_x viene descritta dalla (1) ed è già stata risolta. Non dimentichiamo, comunque, che essa esiste e dovrà poi essere tenuta in conto! Cosa succede alla componente u_y?

In altre parole, come si trasforma la componente della velocità u’ secondo y’ (com'è vista da S’), quando viene vista dal sistema S. Essa deve perdere l’indice e diventare una u_y.

La risposta potrebbe sembrare ovvia: “Sappiamo che, anche nella RR, y = y’ (trasformazioni di Lorentz) e, quindi, anche le componenti delle velocità relative a questi assi devono rimanere uguali come succede per Galileo”. No, assolutamente no! Una velocità è data dal rapporto tra una lunghezza e un tempo e se è vero che le lunghezze secondo y si mantengono non è affatto vero che il tempo di S’ visto da S si mantenga. Anzi, sappiamo benissimo che cambia e come! Il che vuol dire che deve cambiare anche la componente della velocità ortogonale alla direzione del moto relativo dei due sistemi.

Consideriamo il caso più generale, ossia quello in cui stiamo proprio parlando di una componente di una velocità u’, diretta comunque, e separata nelle sue due componenti.

La velocità ortogonale u’_y, vista da S diventa una u_{y ,} data dalla formula

u_y = u’_y (1 – v²/c²)^1/2/(1 + v u’_x/c²)    …. (2)

Non dobbiamo certo stupirci che compaia la velocità v e la componente u’_x (d’altra parte basta ricordare che tempo e coordinata x sono strettamente collegati… se cambia il primo deve cambiare anche la seconda, come ci dicono sempre le trasformazioni di Lorentz).

Tuttavia, la formula si semplifica non poco se la velocità u’ di P’ è diretta SOLO in direzione ortogonale, rispetto al moto di S’. In questo caso u’ coincide con u’_y e abbiamo immediatamente che u’_x = 0. La formula di prima si trasforma nella più semplice e intuitiva:

u_y = u^’_y (1 – v²/c²)^1/2     …. (3)

In parole povere, dato che il termine sotto radice quadrata è sempre minore di uno, la componente ortogonale della velocità dell’oggetto P’, lanciato all’interno dell’astronave ortogonalmente al moto dell’astronave, viene vista accorciarsi da S, rispetto a quella u’_y che vede il capitano in S’. E più la velocità dell’astronave è grande è più la componente ortogonale della velocità dell’oggetto P’, visto dal papallo S, appare diminuire. Tuttavia, stiamo ben attenti che la velocità totale vista da S è qualcosa di ben diverso, dato che l’astronave continua a viaggiare sempre a velocità v.

Abbiamo visto che, sia per una velocità con direzione qualsiasi che per una velocità soltanto ortogonale dell’oggetto P’, la componente della velocità u_y vista da S si riduce rispetto a quella u’_y vista da S’. Nel caso che la velocità abbia direzione qualsiasi, questa riduzione è regolata da due fattori di correzione (2): uno è relativo solo alla velocità del’astronave v ed è dato da (1 – v²/c²)^1/2 e l’altro anche dalla componente della velocità di P’ lungo x’ (u’_x) ed è dato da 1/(1 + v u’_x/c²) . Nel caso che la velocità di P’ sia solo diretta lungo l’asse y’ (3), il fattore di correzione si riduce solo al primo, ossia a (1 – v²/c²)^1/2. L’altro, ovviamente, si riduce a 1, dato che u’_x = 0.

La componente u_x, se esiste u’_x, segue sempre la contrazione relativistica data dalla (1). Se u’_x è uguale azero, u_x si riduce alla velocità v tra i due sistemi.

Come già detto, la parte appena conclusa risponde praticamente al quiz proposto da poco  e per darne una visione grafica completa ci possiamo riferire alla Fig. 2, in cui tutto ciò che è visto dal sistema S’ è rappresentato in blu (con l’apice), mentre ciò che è visto da S è rappresentato in rosso (senza apice). Teniamo presente che le contrazioni dei vari vettori sono state introdotte “a caso” e non corrispondono a una qualche scelta particolare delle velocità. Insomma, la figura è solo qualitativa, almeno per quanto riguarda la parte relativa a Einstein (RR). Ovviamente, la velocità v relativa alla parte sinistra deve essere decisamente più piccola della v della parte destra!

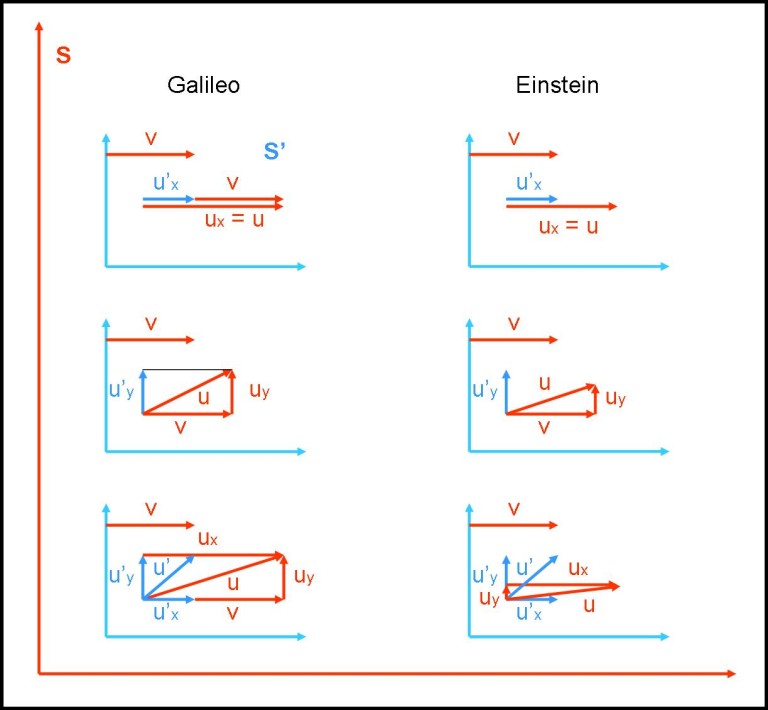
Con queste nozioni acquisite, siamo in grado di affrontare la dinamica relativistica e vedere come le assunzioni della RR stravolgano la dinamica newtoniana, sempre e soltanto se le velocità si avvicinano di molto a quella della luce.