Risolvere questo QUIZ si riduce a brevissimi calcoli che non hanno nemmeno bisogno di trigonometria, viste le distanze in gioco e la piccolezza degli angoli… La parallasse domina, ma si ripete ogni anno.

Impostiamo subito la Fig.1, che illustra la situazione. Come detto, consideriamo l’orbita del nono pianeta circolare con raggio pari a 600 Unità Astronomiche. Cominciamo subito con qualche piccola approssimazione. Conoscendo la velocità angolare del pianeta rispetto al Sole, dovremmo riportarla alla Terra che gira attorno a lui. Gli angoli sono leggermente diversi, ma la differenza è del tutto trascurabile. Consideriamo, perciò, il movimento angolare del pianeta visto dalla Terra dopo una sua rivoluzione attorno al Sole (movimento angolare annuo) uguale a quello visto dal Sole nello stesso periodo di tempo.

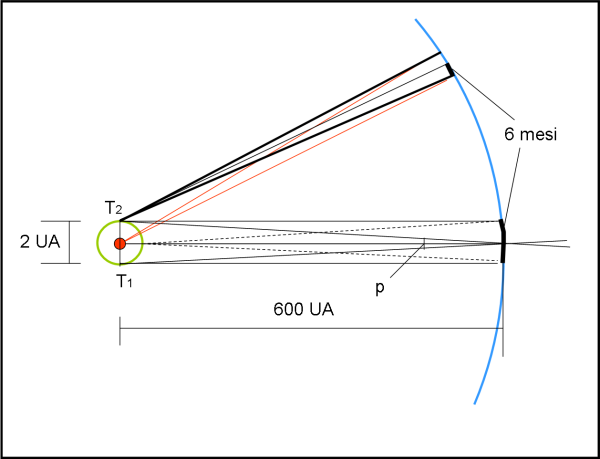
Per trovare la velocità angolare costante del pianeta rispetto al Sole, basta dividere 360° per il periodo di rivoluzione del nono pianeta. Ma, il periodo P si ottiene direttamente dalla terza legge di Keplero (la costante vale 1) se si usano come unità di misura l’anno e l’unità astronomica. Si ha:

P = (r³)^1/2

Nel nostro caso r = 600 UA, per cui:

P = 14 700 anni.

Per sapere l’angolo percorso in sei mesi (la distanza angolare da paragonare con la parallasse annua), basta scrivere la proporzione:

360/14700 = x/0.5

x = 360 0.5/14700 = 0.012° = 0.73’

Per averne un’idea, pensiamo che il diametro angolare della Luna è di circa 30’. Non si può dire che non viaggi come una lumaca!

Se, inoltre, pensiamo che l’orbita è tutt’altro che circolare e che lui si dovrebbe trovare vicino all’afelio, ne viene fuori un angolo decisamente più piccolo.

Passiamo alla parallasse annua. In poche parole, immaginiamo il pianeta fermo e calcoliamo l’angolo p sotto cui lui vede l’asse dell’orbita terrestre che è uguale a 2 UA. Questo angolo corrisponde a quello descritto in sei mesi (ecco perché prima avevamo considerato sei mesi…).

Ne segue, senza bisogno di introdurre tangenti o seni:

p = 2/600 = 0.003 rad = 0.19° = 11.4’

2 UA è il lato minore e 600 UA è il lato maggiore del triangolo pianeta-Terra₁-Terra₂. Questo angolo rappresenta molto bene lo spostamento angolare del pianeta in sei mesi dovuto solo al movimento della Terra attorno al Sole.

Sono perciò da paragonare tra loro 0.012° e 0.19°. Ne segue che durante sei mesi il movimento di parallasse è ben 16 volte superiore a quello dovuto al moto proprio del pianeta attorno al Sole.

Anche per la parallasse bisogna tener conto che le 600 UA devono essere allungate, per un orbita ellittica. Tuttavia, ponendo pure che l’eccentricità sia di 0.5, avremmo una distanza di 900 UA che comporterebbe, comunque, un valore di parallasse di 0.13°, sempre nettamente superiore a quello dovuto al moto (che oltretutto dovrebbe essere diminuito).

In poche parole, la parallasse annua è nettamente favorita per vedere muoversi una strana stellina di 22 mag in mezzo a tante altre vere stelle ben più lontane e praticamente ferme. Come dice giustamente Paolo, va detto che il moto di parallasse è sempre lo stesso (avanti e indietro), mentre quello del moto proprio va sempre in una certa direzione. In realtà, quello che si dovrebbe vedere è la solita curva annodata “a cappi” che caratterizza il moto di un pianeta visto da Terra, come rappresentato in Fig. 2 per il vicino e rapidissimo Plutone.

Il movimento, comunque, è alla portata di una strumentazione odierna anche di tipo ultra amatoriale. Il problema è trovare questa debole stellina così ballerina, ma senza una caratteristica che la diversifichi rispetto alle sorelline veramente lontane. Altro che la solita galassia vista (o solo immaginata) con il bordo dell’occhio… Questa sì che sarebbe una scoperta e un bell’aiuto alla vera astronomia!