Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Conserviamo e non uguagliamo

Riassumiamo e fermiamoci a pensare al concetto che sta alla base di tutta questa rivoluzione. Ciò che la cinematica relativistica ha voluto fare è, in fondo, solo e soltanto non permettere che qualcosa possa superare la velocità della luce. Per far ciò è stato necessario allungare tempi e accorciare lunghezze e, per quanto ci interessa d’ora in poi, accorciare le velocità ortogonali alla direzione del moto. Il punto chiave di tutto è proprio questa conclusione.

Basterebbe solo quest’ultimo concetto per dimostrare in modo quasi immediato che sotto l’ipotesi della RR la quantità di moto, la “mia” grandezza preferita (la lumachina della Fisica Addormentata nel Bosco…), non può più essere definita con la formula newtoniana che dice:

q = mv

Se mantenessimo questa definizione, la RR ci porterebbe alla sua NON conservazione, uno dei capisaldi di tutta la fisica, che nemmeno Einstein ha intenzione di distruggere. Non ci resta che dimostrare la sua non conservazione e correre ai ripari.

Dimostrare la non conservazione della quantità di moto definita con la fisica classica, ma immersa nel mondo relativistico, non è gioco banale come potrebbe sembrare a prima vista. Cosa altrettanto non immediata è verificare che una nuova definizione della quantità di moto la conservi anche in campo relativistico. Diffidiamo di tentativi semplificati che mischiano capra e cavoli.

Non vogliamo nemmeno far notare gli “errori” più frequenti perché comporterebbero una sicura confusione (ne abbiamo accennato nel quiz). Ciò che è importante capire molto bene è che siamo costretti a cambiare la definizione di quantità di moto, ossia da q = mv (definizione classica) dobbiamo passare a qualcosa del tipo q^R = m'v, dove m’ si possa considerare una variabile che cresca con la velocità a cui viaggia il corpo visto da un qualsiasi sistema di riferimento inerziale.

Non vogliamo assolutamente uguagliare la quantità di moto classica con quella relativistica, ma dimostrare che quella relativistica si conserva e che solo per velocità molto basse coincide con quella classica.

Niente metodi semplificati, quindi, ma affrontiamo, senza esitazioni, un esperimento leggermente più complesso, che risulta del tutto ovvio, emozionante e appagante, se seguito con grande attenzione e molta calma. D’altra parte, chi è interessato a entrare nel mondo sconvolgente e rivoluzionario della dinamica relativistica, nel mondo in cui energia e massa si abbracciano strettamente come indica (solo parzialmente) la troppo celebre formula di Einstein, nel mondo che è poi quello che ci circonda (le scuole prima o poi lo capiranno?), non può esimersi dall’accettare un piccolo sforzo.

Abbiamo cercato, al pari del tempo relativistico, di fare scorrere i vari passaggi con molta lentezza, quasi al rallentatore, invitando a fermarsi a riflettere nei punti più critici. Infondo, è solo necessario comprendere il concetto logico dei vari passaggi, dato che la matematica è veramente ridicola e alla portata di qualsiasi studente (forse anche di scuola media, se ricordo bene). Siamo anche sicuri che, fatti i dovuti arrangiamenti, l’intera problematica possa essere anche spiegata a livello papalliano…

Nessuna paura, quindi, dato che le difficoltà sono alla portata di tutti coloro che abbiano voglia di imparare e che abbiano digerito, più o meno, la cinematica della Relatività Ristretta (RR).

Due palline e un urto elastico galileiano

Iniziamo a descrivere un esperimento relativo a un urto elastico tra due corpi. In questo tipo di fenomeno, la quantità di moto dà il meglio di sé. Cerchiamo di stare bene attenti ai colori delle varie frecce e delle componenti delle velocità che compariranno nelle figure. Nel testo aggiungeremo qualche indice per supplire ai colori, ma l’importante è mantenere una visione unitaria.

Tutto ciò che si riferisce a un sistema di riferimento S’ viene segnato in blu, tutto ciò che si riferisce a un sistema di riferimento S viene segnato in rosso. Ciò che succede lo vediamo da S. Il che vuol dire che tutte le componenti delle velocità di S’ devono, comunque, essere disegnate in rosso, dato che sono quelle di S’ viste da S. All’inizio tutte queste parole sembrano inutili (e lo sono, in effetti), ma introducendo la RR le cose cambiano e non dobbiamo farci prendere in contropiede.

Un solo sistema di riferimento

Questa prima parte la vediamo descritta nella Fig. 3.

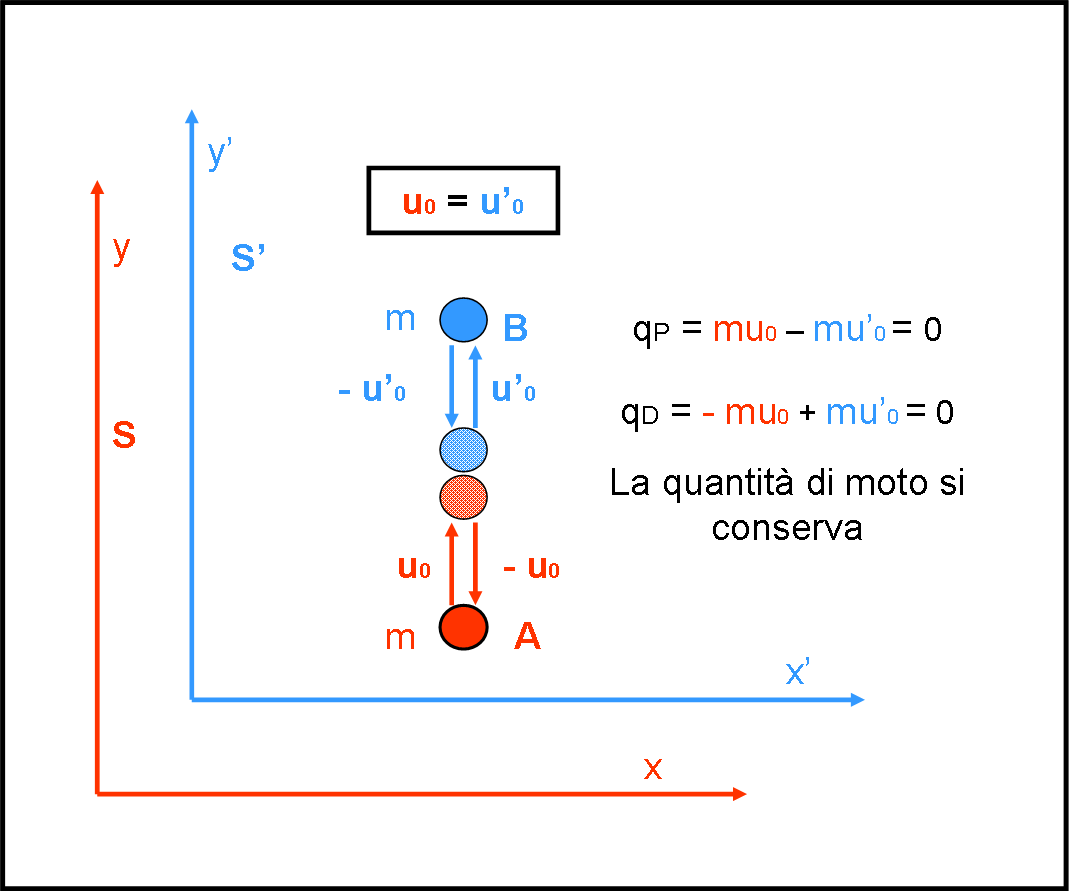
Due palline A (rossa) e B(blu) hanno la stessa massa m. A appartiene al sistema di riferimento S e B al sistema di riferimento S’. I due sistemi sono fermi uno rispetto all’altro. I due osservatori lanciano le loro palline lungo gli assi y e y’ (coincidenti), con la stessa velocità di modulo u₀. Le due palline si urtano nel punto di mezzo.

La quantità di moto è un vettore, ma noi trattiamo d'ora in poi con le sue componenti lungo gli assi e, quindi, possiamo limitarci ai moduli. Ogni pallina ha una certa quantità di moto: A ha una quantità di moto mu₀ e B ha una quantità di moto – mu₀. Inseriamo i pedici P e D per distinguere la quantità di moto Prima e Dopo l'urto.Il sistema delle due palline ha quindi, prima dell’urto, un momento totale della quantità di moto dato da:

q_P = mu₀ – mu₀ = 0

Dopo l’urto (perfettamente elastico), le palline invertono la loro velocità, per cui la pallina A acquista una quantità di moto – mu₀, mentre la pallina B acquista una quantità di moto mu₀. La quantità di moto del sistema dopo l’urto diventa:

q_D = – mu₀ + mu₀ = 0.

Possiamo concludere che la quantità di moto si è conservata. Tutto secondo le previsioni, dato che il sistema è isolato e non vi sono forze esterne a disturbarlo.

Qualche considerazione sui colori…

Le frecce viste da S’ sono blu, le frecce viste da S sono rosse. I due sistemi sono fermi e, quindi, i colori possono essere tranquillamente scambiati o essere considerati uguali. In fondo, il sistema di riferimento è uno solo poiché S = S’. Analogamente, è del tutto equivalente scrivere u’₀ o u₀, dato che anche loro sono uguali. Guardiamo bene la figura precedente e cerchiamo di capire perfettamente la possibilità di scambiare u₀ con u’₀ e i loro colori.

S’ si muove lentamente, seguendo Galileo

Mettiamo, adesso, in movimento il sistema S’ con una certa velocità v di trascinamento rispetto a S lungo l’asse x (ossia facciamo scorrere l’asse x’ lungo x con una velocità v), come descritto in Fig. 4. La velocità v non ha apice e viene colorata in rosso, dato che viene “vista” solo da S.

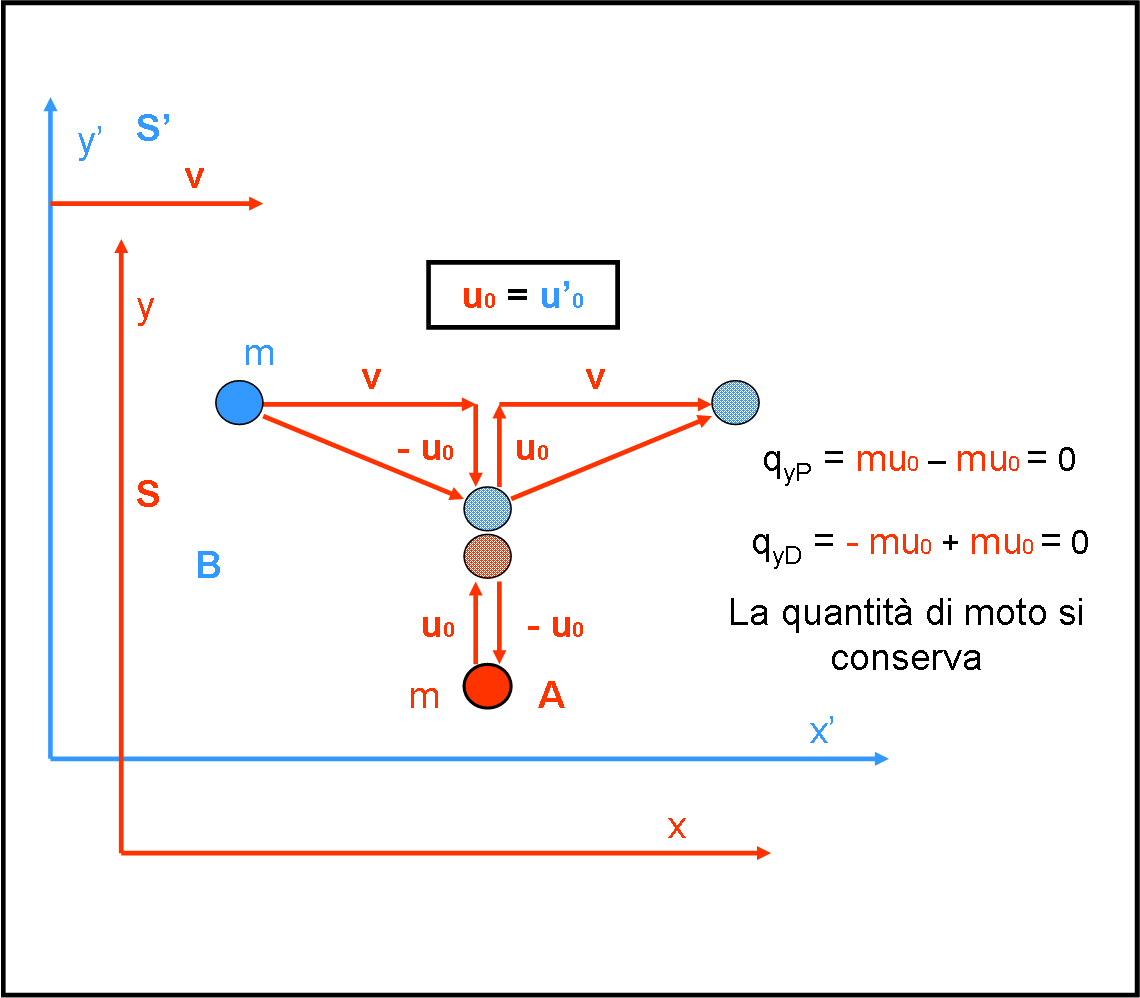
Osserviamo, come sempre, lo svolgimento dell’esperimento dal riferimento S. Le cose, in ambito galileiano, non cambiano. La velocità u₀ rimane la stessa di prima (u₀ = u’₀), vista da entrambi i sistemi. Tuttavia, coloriamo in rosso anche la velocità relativa alla pallina B di S’, dato che la stiamo vedendo da S. La perfetta uguaglianza dipende dal fatto che per Galileo le velocità ortogonali al movimento tra i due sistemi non vengono assolutamente influenzate.

Le due palline si urtano come prima, anche se S continua a vedere A andare verso l’alto e poi tornare verso il basso, mentre la B di S’ è vista percorrere una linea spezzata, data dalla composizione della velocità di trascinamento v dei due sistemi e della velocità u₀ = u₀’ della pallina. Comprendiamo bene questa figura, mi raccomando. La pallina B viene lanciata in S’, ma prima che arrivi a urtare la A, lanciata in S, deve viaggiare anche in senso orizzontale con  velocità v.

Ovviamente, la faccenda se vista da B in S’ sarebbe perfettamente simmetrica. Per S’ sarebbe S che si muove con velocità – v, ma la conclusione sarebbe la stessa, anche se invertita. Nessun problema, quindi, a lavorare solo su S.

Possiamo concludere che, anche con il sistema S’ in movimento, la quantità di moto delle palline rimane inalterato, dato che sia le masse che le velocità sono rimaste identiche. La quantità di moto si conserva nell’urto.

In realtà, abbiamo considerato solo la componente verticale della quantità di moto totale (la quantità di moto è un vettore, non dimentichiamolo). Dovevamo considerare anche quella orizzontale? Teoricamente sì, ma questa si mantiene e si manterrà sempre. Possiamo anche dimostralo facilmente.

Prima dell’urto, essa vale:

q_Px =  0 + mv

La quantità di moto della pallina rossa per il sistema S è ovviamente ZERO, dato che la pallina non si muove lungo l’asse orizzontale. La quantità di moto orizzontale della pallina blu, vista da S, è data da mv.

Dopo l’urto, essa vale:

q_Dx = 0 + mv

Nulla è cambiato, dato che, sebbene la pallina A inverta il suo moto, essa continua a muoversi solo secondo l’asse y: la sua componente orizzontale rimane ZERO. La pallina blu, invece, continua a viaggiare, rispetto a S, con velocità v nella stessa direzione di prima.

Notiamo, già adesso, che questa componente non interessa nemmeno se si applica la RR. Anche in quel caso la velocità orizzontale della pallina rimane sempre v (la velocità di trascinamento vista da S). Non esiste una composizione di velocità orizzontale. In altre parole, la componente orizzontale può sempre essere trascurata e ci si può dedicare solo e soltanto alla componente verticale. Fermiamoci un attimo e pensiamo a questa conclusione: essa DEVE apparire del tutto logica. OK? Possiamo proseguire…