La risposta alla domanda è estremamente semplice e non dipende assolutamente dalle distanze e dalle velocità che abbiamo scelto. L’unica cosa importante è che la velocità del papalelettrone sia maggiore di quella dei due papalli. In queste condizioni possiamo tranquillamente dire che il numero di viaggi che è costretto a fare il papalelettrone è INFINITO. Ogni viaggio, da un papallo all’altro, diventa sempre più corto e dopo un certo tempo ben determinato i due papalli si incontrano e quindi anche il papalelettrone è obbligato a fermarsi (anche se ha dimensioni nulle), ma dobbiamo accettare che il numero di tragitti fatti, avanti e indietro, sia infinito.

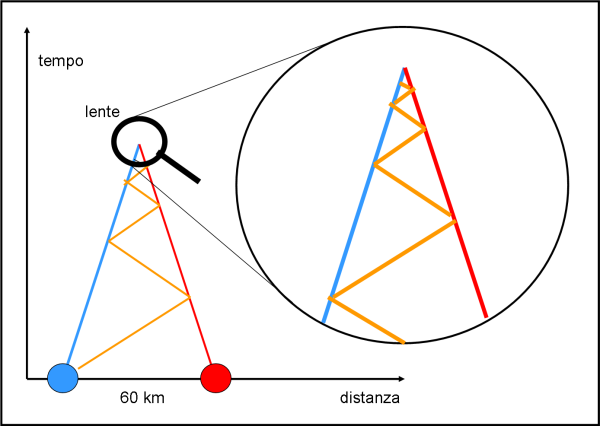
Se disegniamo la distanza dei papalli in funzione del tempo, essa continua a diminuire e il papalelettrone continua a rimbalzare in uno spazio sempre più stretto (Fig. 1). Tuttavia, se utilizziamo una lente e andiamo a vedere cosa succede mentre ci si avvicina all’urto finale dei due papalli, ci accorgiamo che la figura non cambia e l’andamento si ripete fino all’infinito. Siamo di fronte al solito scontro tra zero e infinito, che ci era già servito all’inizio del corso di matematica. Il tratto percorso dal papalelettrone tende a zero (diventa infinitesimo), mentre il numero di tratti percorsi tende a infinito.

Se si riflette un attimo, il gioco dei due papalli ricorda moltissimo il celeberrimo paradosso di Zenone. In quel caso, si dice che se una tartaruga, molto più lenta di Achille piè veloce, parte prima di lui, il grande guerriero greco non riuscirà mai a raggiungerla. Infatti, nel tempo che Achille parte di gran carriera e raggiunge la tartaruga, quest’ultima si è mossa di una certa quantità in avanti. Achille supera in un attimo anche questa piccola lunghezza, ma la tartaruga, nel frattempo, ha proseguito… e via dicendo. In altre parole, la tartaruga è sempre di una quantità, seppure infinitesima, davanti ad Achille. Di questo paradosso ne abbiamo parlato a lungo QUI e QUI.

Il nostro caso papalliano è molto simile, anche se sembrerebbe non esistere un paradosso, dato che il senso comune direbbe che il papalelettrone deve fermarsi dopo un certo numero di viaggi. In realtà, invece, la situazione è analoga: in entrambi i casi dobbiamo tenere conto che aggiungere, a una certa quantità, una quantità sempre più piccola porta a un risultato finale ben determinato e non a infinito.

In altre parole, sommare infinite volte delle quantità sempre più piccole non dà come risultato infinito ma un numero finito.

L’assurdità dei due papalli che si urtano  sta proprio nell’accettare che per ottenere la fermata del papalelettrone è necessario che questo rimbalzi infinite volte, anche se in un tempo sicuramente limitato.

Cerchiamo di capire meglio questa apparente assurdità. Se io dicessi: “Contate ogni volta che il papalelettrone tocca uno dei due papalli”, voi comincereste a contare: “Uno, due, tre, quattro, ecc., ecc.” in attesa che tutto finisca.

Vi accorgereste però che il numero continua a salire e non ha mai fine. Vi arrabbiereste non poco dicendo: “E’ impossibile! Se continuo a sommare tragitti, ossia intervalli di tempo, per un  numero infinite di volte, l’elettrone deve automaticamente impiegare un tempo infinito per terminare la sua corsa. E, invece, vediamo benissimo che dopo un certo tempo ben definito, che dipende SOLO dalla distanza e dalla velocità dei papalli, la corsa deve avere termine. E’ assurdo che sommare infinite volte un qualcosa dia come risultato un numero finito!”

L’errore che si commette è lo stesso di Achille e la tartaruga. Voi non  sommate quantità costanti, ma quantità sempre più piccole di quella precedente. In  questo caso, ribadiamo ancora, un numero infinito di volte una quantità che tende a diventare zero dà come risultato un valore finito e non infinito. Non dovreste contare “uno, due, tre, quattro,…” sempre alla stessa velocità, come se fossero secondi di tempo, ma dovreste contare accelerando le parole, dato che l’intervallo di tempo di ogni tragitto si fa sempre più corto e tende a diventare zero.

Vi sono vari modi per dimostrare in modo analitico questo fatto (lo avevamo già fatto per il paradosso di Zenone) e per andare avanti con le domande e le risposte, tipo: quanta strada ha percorso il papalelettrone prima di rimanere incastrato tra i due papalli? E ancora: cosa succede se le dimensioni del papalelettrone non sono nulle?

Il giochino diventa un ottimo strumento didattico per analizzare la situazione generale (velocità e distanze qualsiasi) sia con mezzi puramente matematici e/o geometrici (normalmente più rapidi), sia attraverso gli sviluppi in serie, magari non indispensabili, ma interessanti per  comprenderne appieno il significato.

Nel prossimo articolo, con un asterisco in più, Umberto, Paolo ed io daremo qualche esempio dei calcoli fattibili, anche se ci accorgeremo che le possibilità sono molte. La matematica è uno splendido linguaggio e quindi per spiegare un qualcosa di fisico può usare parole e frasi anche diverse. L’importante è che la conclusione sia la stessa.

Ah… posso dirvi che il papalelettrone  si è divertito un sacco e non vorrebbe mai smettere di giocare. Eh sì, Papalla è proprio un mondo fantastico!

Mentre noi abbiamo sviscerato il viaggio di un elettrone che rimbalza tra due papalli, Gatto Gualtiero avrebbe voluto spiegarci come calcolare in un battibaleno quanta strada percorre una mosca che vola avanti e indietro tra due treni... ma aveva troppo sonno e, per questa volta, si è fatto sostituire dalla sua zampa destra Alan che, tuttavia, si è dimostrato all'altezza! Ecco QUI il loro video.