Categorie: Relatività
Tags: conservazione quantità di moto relativistica dinamica relativistica relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:20
Dinamica Relativistica. 1: Cambiamo la quantità di moto. 4 ***
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Bene, cominciamo a vedere qual è la velocità totale di entrambe le palline, quando vengono viste dal sistema S.
Consideriamo la Fig. 6 (uguale alla 5), ponendo particolare attenzione al triangolo indicato dalla freccia.
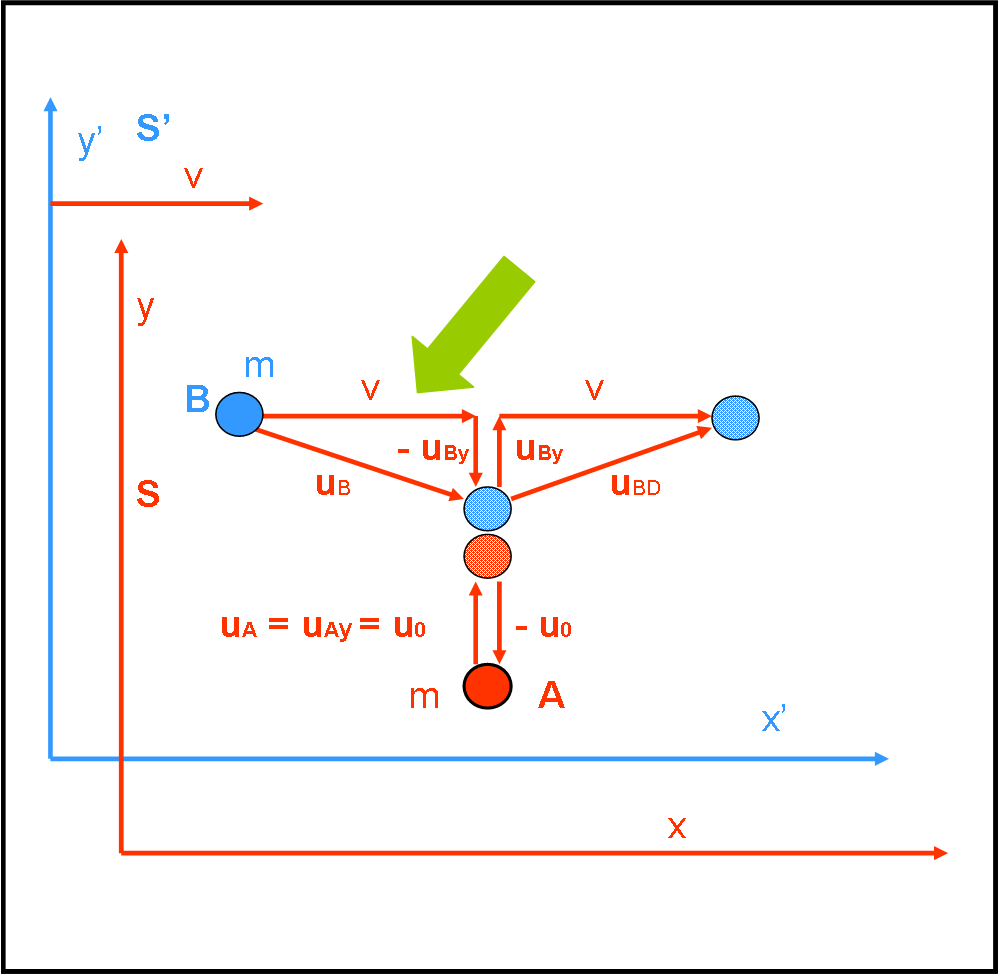
Attenzione! E’ cosa ben diversa da quella fatta finora, in cui ci siamo occupati solo della componente verticale, dato che era quella che decideva la conservazione oppure no della quantità di moto. Adesso, volendo cambiare la definizione della quantità di moto, facendo variare la massa in funzione della velocità di entrambe le palline, siamo obbligati a calcolare proprio queste velocità per poter cambiare la massa. Alla fine, torneremo di nuovo alla sola componente verticale che sarà però quella corretta.
Cominciamo con la parte più facile: la velocità uA della pallina rossa. Beh… essa rimane sempre la stessa, ossia:
uA = uAy = u0
Tocca adesso alla velocità uB della pallina blu vista sempre da S. Cominciamo a verificare se è veramente più grande di uA.
Essa altro non è che la composizione delle velocità lungo x e lungo y della pallina blu (teorema di Pitagora), viste da S, ossia:
uB2 = uBx2 + uBy2 = v2 + (- u0(1 – v2/c2)1/2)2 = v2 + u02(1 – v2/c2)
uB2 = v2 + u02 – u02 v2/c2 = u02 + v2(1 – u02/c2) > u20 = u2A
Risulta chiaro che uB è maggiore di uA
Ricordiamoci bene questo passaggio:
uB2 = v2 + u02 – u02 v2/c2 …. (5)
ci tornerà molto utile tra poco.
Definiamo ora una nuova massa tale che, in generale, valga:
mW = m0 /(1 – w2/c2)1/2
dove m0 è la massa a riposo, ossia quella relativa al corpo fermo, mentre mW è la massa quando il corpo si muove alla velocità w .
La nuova quantità di moto relativistica diventa, allora:
qR = mW w = m0w/(1 – w2/c2)1/2
Notiamo, nuovamente, che la massa dipende direttamente dalla velocità w dell’oggetto (il pedice si riferisce alla loro effettiva velocità vista da un certo sistema di riferimento)
Inseriamo le nuove masse nelle quantità di moto del nostro caso . Abbiamo (come al solito il pedice P indica “prima dell’urto”):
qRPA = muAuA = m0uAy/(1 – uA2/c2)1/2 = m0u0/(1 – u02/c2)1/2
qRPB = muBuB = m0uB/(1 – uB2/c2)1/2
Tuttavia, a noi interessano solo le componenti verticali delle due quantità di moto relativistiche, ossia qRPAy e qRPBy. Ricordiamo anche che qRPA = qRPAy.
qRPAy = m0uAy/(1 – uA2/c2)1/2 = m0u0/(1 – u02/c2)1/2
qRPBy = - m0uBy/(1 – uB2/c2)1/2
Notiamo bene quello che abbiamo fatto: la massa corretta è definita sulla base della velocità uB della pallina, ma la componente della velocità che stiamo considerando, per il calcolo della quantità di moto verticale, è solo quella verticale. Non confondiamoci, mi raccomando…
Possiamo anche scrivere (ricordando la (4)):
qRPBy = - m0uBy/(1 – uB2/c2)1/2 = - m0u0(1 – v2/c2)1/2/(1 – uB2/c2)1/2 …. (6)
Divertiamoci, adesso, con semplici passaggi algebrici… e niente paura, dato che basta seguirli passo dopo passo.
Partiamo dalla (5):
uB2 = v2 + u02 – u02 v2/c2
uB2/c2 = v2/c2 + u02 /c2 - u02 v2/c4
1 - uB2/c2 = 1 - v2/c2 - u02 /c2 + u02 v2/c4 = (1 - v2/c2) - (u02/c2)(1 - v2/c2) = (1 - v2/c2)(1 - u02 /c2)
(1 - uB2/c2)1/2 = (1 - v2/c2)1/2 (1 - u02 /c2)1/2
Nessun problema, vero? Abbiamo solo diviso per una stessa quantità, cambiato di segno e aggiunto il numero 1, messo in evidenza un fattore comune ed eseguita la radice quadrata.
Sostituendo nella (6), otteniamo:
qRPBy = - m0u0(1 – v2/c2)1/2/((1 - v2/c2)1/2 (1 - u02 /c2)1/2)
qRPBy = - m0u0/(1 - u02 /c2)1/2
Possiamo, finalmente, calcolare la componente verticale della quantità di moto totale prima dell’urto:
qRPAy + qRPBy = m0u0/(1 – u02/c2)1/2 - m0u0/(1 - u02 /c2)1/2 = 0
Fantastico, soprattutto perché dopo l’urto, tutto rimane simmetrico e vale ancora ZERO.
La quantità di moto si è conservata! La nuova quantità di moto relativistica qR funziona e possiamo proprio definirla, per una velocità w qualsiasi:
qR = m w = m0w/(1 – w2/c2)1/2
Non ci resta che provare che per velocità decisamente inferiori a quella della luce, la quantità di moto relativistica diventa quella classica, ossia:
Se w << c, allora qR = q
Beh… questa verifica è immediata
qR = m0w/(1 – w2/c2)1/2
Se w << c
Si ottiene:
qR = m0w = q
Per valori piccoli di u, la quantità di moto relativistica tende a coincidere con quella classica e compare soltanto la massa a riposo.
Concludendo: La quantità di moto relativistica si conserva in tutti i sistemi di riferimento inerziali e per valori piccoli della velocità tende a coincidere con la quantità di moto classica.






20 commenti
adesso finalmente ho capito qual'era la tua paura; che noi prendessimo come fattore correttivo il tanto citato fattore di lorentz) del moto relativo dei due sistemi con velocità v, mentre invece dobbiamo considerare il
del moto relativo dei due sistemi con velocità v, mentre invece dobbiamo considerare il ) dove w è la velocità totale della particella. Conti a parte che devo provare a fare mi sembra perfetto.
dove w è la velocità totale della particella. Conti a parte che devo provare a fare mi sembra perfetto.
proprio così, caro Umberto... Troppe volte ho visto inserire la velocità di trascinamento senza puntualizzare la situazione. In certi casi può anche essere giusto (se il corpo non si muove di per sé, l'unica velocità è quella di trascinamento... ma guai a generalizzare!). Volevo, però, essere sicuro di descrivere un metodo che mettesse bene in evidenza la vera natura della velocità che entra nella massa... Ed è per quello che ho lavorato parecchio sulla scelta finale...
Penso però che l'articolo più duro rimanga il secondo; qui abbiamo una definizione di massa relativistica che tramite dei calcoli ci conferma la conservazione.
Ma la strada era già spianata dal calcolo delle componenti. Bisogna aver compreso bene il principio di relatività per giustificarlo bene. Io ancora mi confondo.
scusa, intendevo il terzo articolo
Ma il terzo articolo non fa altro che applicare la composizione relativistica delle velocità, Solo quella verticale, oltretutto. Non riesco proprio a capire dove trovi la difficoltà... Vorrei aiutarti di più, ma non so proprio come fare (assodato che hai compreso come calcolare la composizione delle velocità, ovviamente...)
era il discorso di ieri..ma non ti preoccupare assodato che il fenomeno deve essere lo stesso nei due sistemi tutto torna. Non é necessario tornare più si questo problema .
OK... in ogni modo, se ti viene qualche nuovo dubbio... son o qui
dunque..adesso abbiamo introdotto la massa relativistica che é funzione della velocità totale per garantire la conservazione della qdm in urto elastico; il prossimo passo sarà garantire la conservazione dell'energia cinetica nell'urto? O useremo semplicemente la nuova definizione di massa per arrivare alla mc2? Scusa se ti chiedo un anticipo solo concettuale.
Caro Umberto,
Prima bisognerà modificare l'energia cinetica in base a una massa che cambia con la velocità, arrivando alla mc2, e poi si verificherà la sua conservazione in qualsiasi tipo di urto. Prima ancora, però, troveremo come varia la velocità e come si modifica la seconda legge della dinamica.
N.B.: ho preferito togliere l'articolo sulla determinazione alternativa della quantità di moto relativistica. Non solo era poco intuitivo, ma oltretutto era decisamente più limitato rispetto a quello che abbiamo seguito nelle varie puntate. E' inutile creare una possibile confusione aggiuntiva su un argomento già di per sé abbastanza delicato. Ciò che abbiamo fatto basta e avanza e , oltretutto, sarà seguito da un metodo alternativo decisamente più chiaro...
Solo una breve considerazione sulle implicazioni di considerare la massa relativistica……. spesso si sente dire che per accelerare un corpo alla velocità della luce ci vuole un energia infinita….
Ammettiamo di avere un corpo di massa m che viaggia per inerzia ad una certa velocità, inferiore a quella della luce.
La sia Energia cinetica è uguale a: Ec = ½ m v²
Sostituendo ad m, la sua versione relativistica, si ha:
Ec(1) = ½ v² mo/√ (1- v²/c²)
Per accelerare il corpo alla velocità della luce mi serve un’energia paria a :
Ec(2) – Ec(1) = ½ c² mo/√ (1- c²/c²) - ½ v² mo/√ (1- v²/c²)
Ma Ec(2) = ½ c² mo/√ (1- 1) = ½ c² mo/0 = ∞
Ec(2) – Ec(1) = ∞ - Ec(1) = ∞
Qualunque sia l’energia cinetica iniziale per accelerare il corpo dotato di massa alla velocità della luce serve un’energia infinita.... o sbaglio?
Paolo
infatti... l'unica possibilità è avere una massa a riposo uguale a zero. Il che porterebbe a una forma indeterminata.Ed ecco perché il fotone non ha energia infinita... Stai tranquillo che ne parleremo, eccome!
Ti faccio un'ultima domanda; è lecito calcolare con questo metodo la quantità di moto di un'unica pallina vista da due sistemi in moto relativo? ovviamente stiamo parlando della componente trasversale, che nei due sistemi deve essere la stessa, come lo era per Galileo (il moto relativo è longitudinale). E' un pò il discorso dell'elettrone che vede la pallina di massa m andare più piano trasversalmente, e non giustifica la sua quantità di moto trasversale. Vista dal sistema fermo, la pallina che ha solo velocità trasversale ha una quantità di moto che deve essere corretta con la massa relativistica
q=mr U0=m0u0/(1 - u02 /c2)1/2
Vista dal sistema in moto la velocità trasversale deve essere corretta:
chiamiamo q' la quantità vista dal sistema in moto
q'=mr u0(1 – v2/c2)1/2
e poi applicata la massa relativistica
=m0u0(1 – v2/c2)1/2/(1 – uB2/c2)1/2
dove uB è la velocità totale
ma grazie all'eguaglianza che hai ricavato:
(1 - uB2/c2)1/2 = (1 - v2/c2)1/2 (1 - u02 /c2)1/2
q=q' cioè la quantità di moto vista dai due sistemi è la stessa
In pratica potevamo fare a meno dell'urto e considerare una sola pallina di cui studio la quantità di moto trasversale che deve essere la stessa nei due sistemi?
Secondo me,l'errore sta nel fatto che tu non hai usato apici (uo e u'o) per le velocità viste nei due sistemi. Tu li poni uguali, ma questo lo potevi fare nel caso precedente perché avevi un urto come quello ipotizzato nell'esperimento....
non voglio insistere; comunque ho calcolato direttamente le componenti nel secondo riferimento dalle regole di composizione delle velocità, senza passare per gli apici ; U'yo=Uo (1-v^2/c^2) per la y, U'xo=v per la x. Ma non importa, non vorrei andare fuori del tema dell'articolo.
caro Umberto,
forse ci sono... il tuo ragionamento è corretto... tuttavia tu non stai conservando la quantità di moto, ma stai dicendo che la quantità di moto non cambia da un sistema a un altro... Tu stai uguagliando le due quantità di moto. E' il solito vecchio problema...
si, e un altro discorso. Dei tuoi esempi quello che mi ha affascinato di più e quello dell'elettrone che non capisce perché la pallina può rompere il muro la stesso. Così dovrebbe essere giustificato il discorso.
comunque sempre grazie per la disponibilità.
caro Umberto,
non vogliamo che la quantità di moto sia sempre la stessa in tutti i sistemi di riferimento, ma che si conservi.
Pensa di essere fermo: nel tuo sistema la tua qm è zero. Per chi corre a velocità v rispetto a te, la tua quantità di moto non è certo zero.
si è vero; io parlavo di quella trasversale, non certo di quella nella stessa direzione del moto relativo
caro Umberto,
per riassumere il tutto...
Per potere verificare la conservazione della quantità di moto è necessario introdurre un urto elastico o anelastico che sia. Senza questo esperimento non si può verificare la legge.