Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Qualche grafico...

La quantità di moto relativistica si può scrivere come (m è la massa a riposo):

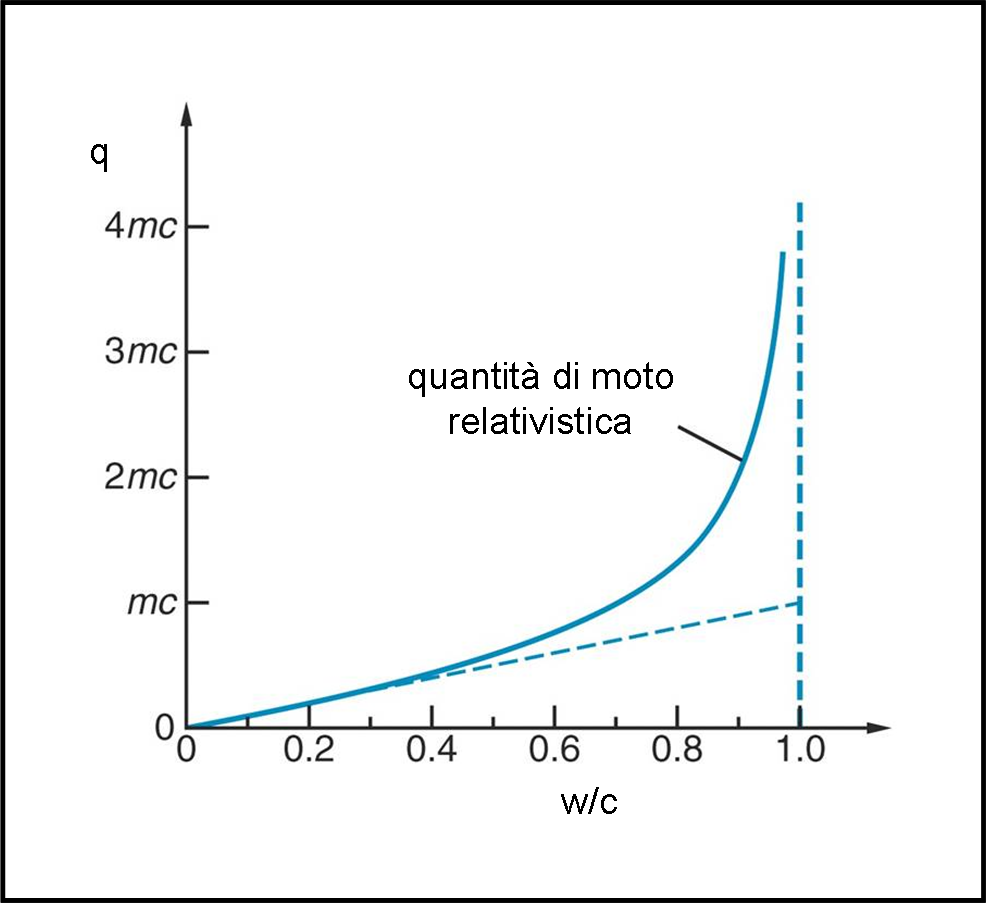
q^R = mw/(1 - w²/c²)^1/2  = m w(c/c)/(1 - w²/c²)^1/2  = mc (w/c)/ (1 - w²/c²)^1/2

Non è difficile riportare, in Fig. 7, la quantità di moto relativistica (in unità di mc), in funzione del rapporto w/c, confrontandola con quella classica.

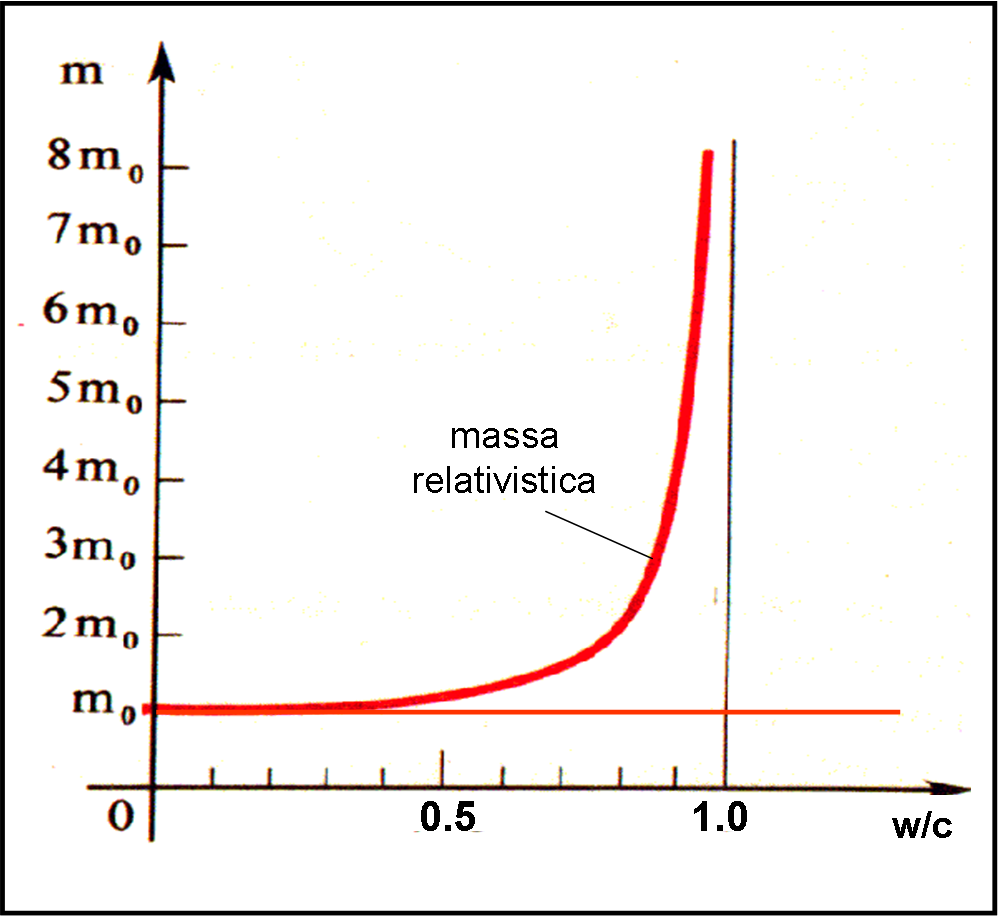
Se preferite, possiamo anche vedere, in Fig. 8, come varia la massa relativistica data da:

m_W = m₀/(1 - w²/c²)^1/2

in funzione dello stesso rapporto w/c e in unità della massa a riposo m₀.

e una sorpresa: la massa non si conserva!

Continuiamo a considerare la massa come una grandezza che cresce con la velocità, pur sapendo i possibili limiti di questa definizione. In realtà, è la quantità di moto che cambia e la variazione viene imputata alla massa. Una massa relativistica diventerà fisicamente “sensata” solo quando si vedrà il suo legame con l’energia. Per adesso, limitiamoci a dimostrare come quanto abbiamo ottenuto finora possa portare a situazioni apparentemente assurde.

Consideriamo un urto perfettamente anelastico tra due palline di uguale massa m che si urtino frontalmente con la stessa velocità di modulo w, ma di segno opposto, come mostrato in Fig. 9 (in alto).

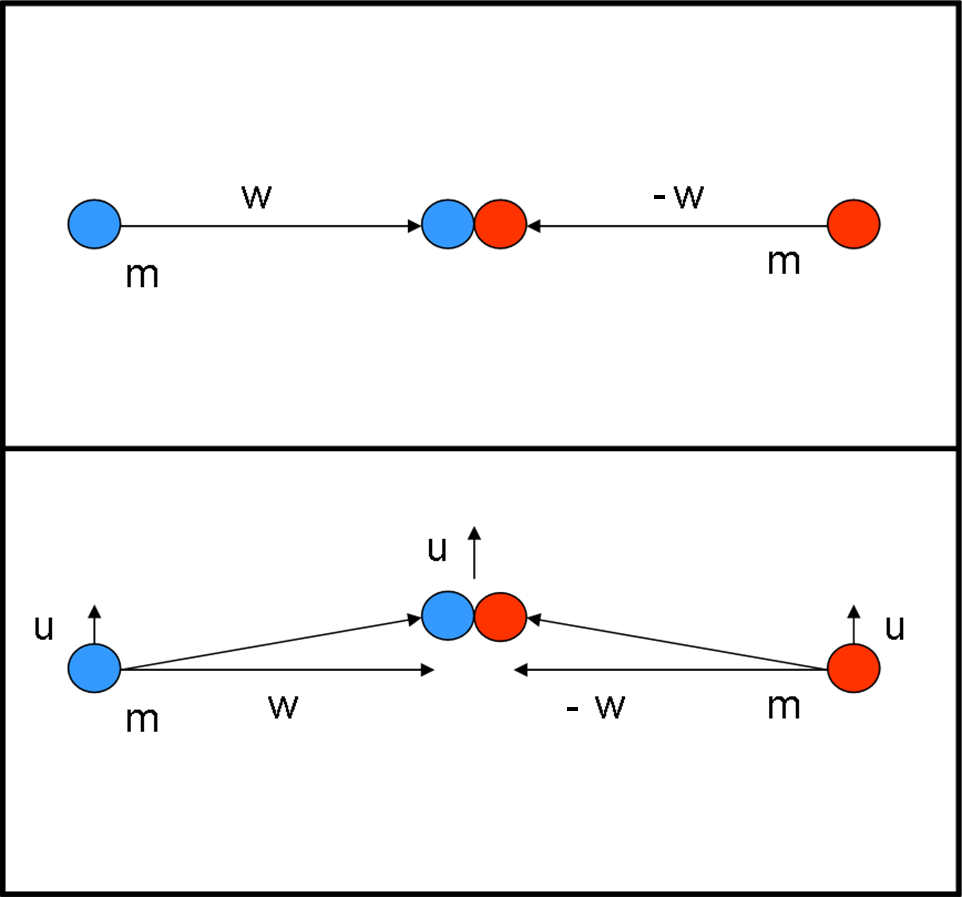
Da quanto abbiamo ricavato le due masse che si muovono a velocità w, devono possedere una massa:

m_w = m₀/(1 – w²/c²)^1/2

Tuttavia, la quantità totale di moto prima dell’urto è uguale a zero e tale deve essere anche dopo l’urto.

Ovviamente:

m_ww – m_ww = 0    (prima dell'urto)

M 0 = 0           (dopo l'urto)

Eseguiamo una piccola variazione all’esperimento (Fig. 9, in basso), imprimendo anche una infinitesima velocità u ortogonale a w. Notate che stiamo usando simboli che niente hanno a che fare con la trattazione dei capitoli scorsi. Le due masse si muovono praticamente a velocità w, per cui la loro massa prima dell’urto deve essere praticamente m_w. La massa dopo l’urto è una certa massa M, che immaginiamo di non conoscere. La quantità di moto verticale prima dell’urto è dato da:

m_Wu + m_Wu = 2m_wu

quella orizzontale è:

m_ww – m_ww = 0

Quella orizzontale si conserva dopo l’urto anelastico dato che le due masse si uniscono, formando M, e si fermano nella direzione di w (massa M con velocità uguale a zero). Succede la stessa cosa del caso precedente: entrambe le quantità di moto orizzontali sono uguali a zero.

Quella verticale,  dopo l'urto, dà luogo a M_uu, ossia a un movimento verso l’alto con velocità u della massa M. 

Per la conservazione deve essere:

M_uu = 2m_wu

Tuttavia, u è talmente piccolo che possiamo considerare M_u = M₀. Ne segue che:

M₀ = 2m_w

“Magnifico!”, diciamo, “Abbiamo appena verificato la conservazione della massa. La massa dopo l’urto è esattamente uguale a due volte la massa di ogni singola pallina!”.

Magnifico… proprio per niente!

Per la conservazione della quantità di moto relativistica, la massa M₀, che è quella di un oggetto praticamente fermo, deve essere uguale a due volte la massa di due oggetti in rapido movimento (m_w). Massa, quest’ ultima, che deve essere decisamente superiore a quelle dell’oggetto fermo (m₀). In parole povere, ma non certo -apparentemente- logiche:

M₀ > 2m₀

Ripetiamo ciò che abbiamo dimostrato: siamo partiti con due masse a riposo (m₀). Le abbiamo scagliate a grande velocità una contro l’altra, producendo un urto perfettamente anelastico. Abbiamo, perciò, ottenuto una nuova massa a riposo (M₀), che è decisamente maggiore della somma di quelle di partenza!

In altre parole, le masse  non si conservano, se vogliamo conservare la quantità di moto relativistica.

In realtà, la conservazione delle masse  continua a essere valida, ma solo se vi è un “abbraccio” molto stretto tra massa relativistica ed energia. Ricordiamo, infatti, che in urto anelastico non si conserva l'energia cinetica, ma se mettiamo insieme massa ed energia le cose potrebbero cambiare in meglio! Ma questo è un  discorso su cui torneremo molto presto… In pratica: le due leggi di conservazione della fisica classica (di massa ed energia) si uniscono in una sola legge, dato che massa ed energia diventano la stessa cosa...