QUIZ destinato ai solutori ... meno abili **

22/02/16

QUIZ destinato ai solutori ... meno abili **

Categorie: Fisica classica Tags: Scritto da: Vincenzo Zappalà Commenti:42

Un gioco molto in voga su Papalla è quello detto del “lancio della papalpalla”. Due papalatleti hanno a disposizione due palline perfettamente uguali che possono lanciare in qualsiasi direzione. Poco importa se la lanciano verso il basso, di lato o verso l’alto: l’importante è che i papalatleti impartiscano alla loro pallina la stessa velocità.  In poche parole, il modulo deve essere identico, ma non la direzione e il verso.

Ogni papalatleta sceglie, senza comunicarlo al suo avversario, la direzione in cui lanciare la sua pallina. Poi si portano entrambi sulla piattaforma di lancio che è posta a una certa altezza h da terra (anzi da… papalla). Al suolo si sistemano i papalgiudici che misurano perfettamente la velocità con cui le palline toccano il terreno. Sono anche i giudici che decidono la velocità di lancio. Ovviamente, dato che la direzione di lancio è qualsiasi, non conta assolutamente il tempo di arrivo, ma solo e soltanto la velocità con cui le palline toccano il suolo. Il vincitore è il papalatleta la cui pallina arriva al suolo con la velocità maggiore.

Va fatto notare che l’accelerazione di gravità su Papalla è esattamente uguale a g, per cui i due papalatleti devono tener conto di questa accelerazione che influisce sicuramente sulla velocità finale.

Si vedono spesso palline lanciate su traiettorie strane, tra le risate del pubblico e degli stessi papalatleti, come mostrato in Fig.1.

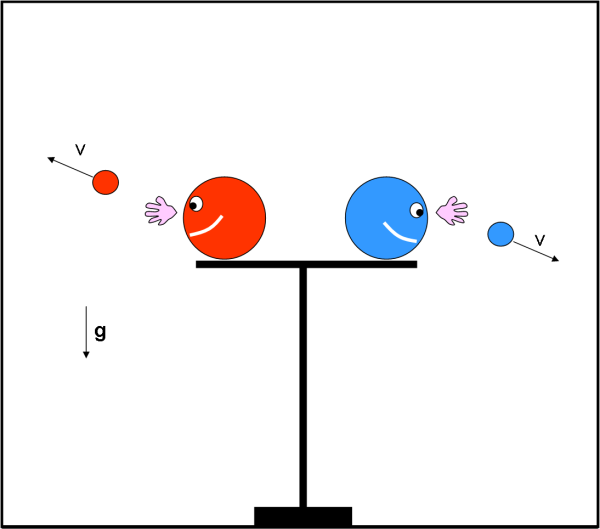
Figura 1
Figura 1

Quella che stiamo per raccontare è una finale dei campionati papalliani di lancio della papalpalla, quindi una gara tra papalatleti molto esperti.

Il primo è papalrosso, famoso per le soluzioni piuttosto elaborate. Il secondo è  papalblu, celebre, invece, per le soluzioni semplici e drastiche. Due campioni con due stili di gara completamente diversi, ma molto efficienti.

Papalrosso decide di sfruttare al massimo g e lancia la sua pallina verso l’alto, in direzione perfettamente perpendicolare al terreno. Salendo più in alto, pensa, acquisterà maggiore velocità al momento dell’impatto al suolo. Papalblu ragiona, invece, in modo opposto e decide di aiutare l’accelerazione g e lancia la pallina proprio verso il basso, anch’egli in direzione perfettamente perpendicolare al terreno. L’inizio della gara è mostrata in Fig. 2.

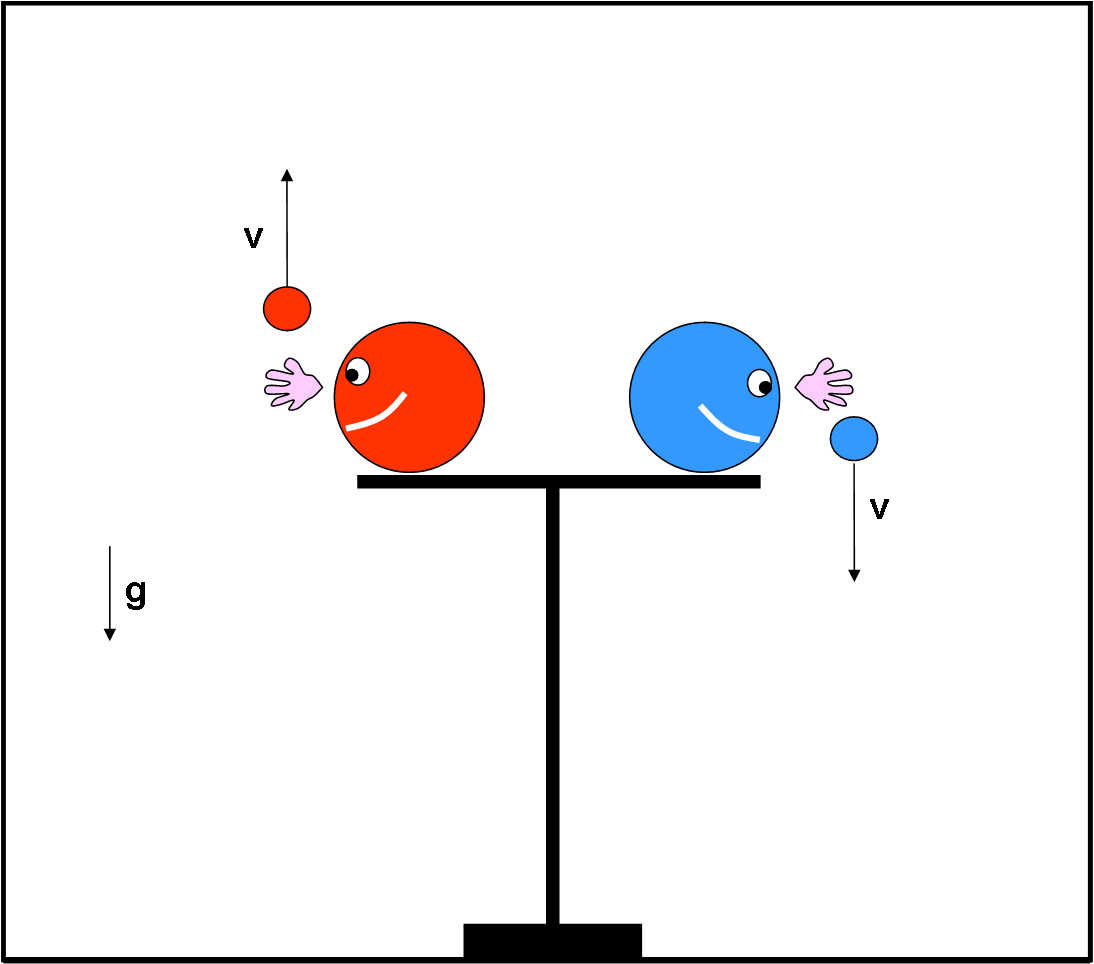
Figura 2
Figura 2

Le domande sono tre: “Che valore deve avere v, in funzione di g, affinché vinca il papalatleta rosso? E quale dovrebbe essere, invece, la velocità v perché vinca il papalatleta blu? E quando (e se) potrebbe avvenire un perfetto pareggio?”

Siamo sicuri che i papallicoli sapranno mostrarci molte variazioni sul tema, dato che hanno assistito a moltissime gare di “lancio della papalpalla”.

Articoli correlati

42 commenti

  1. Alvermag
    22/02/2016 at 13:51

    Mah, se i due lanci avvengono verticalmente (uno verso l'alto e l'altro verso il basso) con lo stesso modulo velocità, mi pare di poter dire che si avrà sempre la condizione di pareggio.

    Consideriamo il papallo rosso che lancia la pallina verso l'alto: inizialmente l'energia potenziale gravitazionale ha un determinato valore, diciamo Ep=m*g*h. A questa devo sommare l'energia cinetica prodotta dal lancio: Ec=0,5*m*v^2. Man mano che la pallina sale l'energia cinetica si trasforma in potenziale, finchè resta solo l'energia potenziale (siamo al cumine della traiettoria). Da lì, la pallina accelera verso il basso "riprendendosi" man mano l'energia cinetica a scapito della potenziale finchè, tornata al punto di partenza, l'energia cinetica avrà riassunto il valore iniziale, come anche la potenziale.

    Il papallo azzurro avrà diretto il suo lancio verso il basso con identica velocità.

    Le due velocità finali (contatto con il terreno) saranno le stesse.

    Mi sembra invece che il discorso sarebbe diverso se le direzioni non fossero verticali, perchè in quel caso dovremmo prendere in considerazione le sole componenti verticali delle velocità impresse: la traiettoria verticale è la più conveniente, a parità di modulo velocità impressa.

    Corretto?

  2. Vincenzo Zappalà
    22/02/2016 at 18:46

    Forza, lanciatevi! Non abbiate paura.... ricordate che chi si mette alla prova, qualsiasi sia il risultato, ha già ottenuto una vittoria. Vale di più un errore conclamato che un silenzio consapevole. Lo stesso Einstein diceva che senza sbagliare non si può fare Scienza. E qui nessuno pretende di trovare un nuovo Einstein (se arriva, però, molto meglio... :mrgreen: ). Basta ricordare il moto di un punto, la sua legge oraria, ma anche meno... basta riflettere... molto meglio di una frase stupida e inutile su facebook... :-P  :-P

  3. Alexander
    22/02/2016 at 20:12

    Sinceramente non sono molto d'accordo con alvy... come primo impatto mi verrebbe da pensare che con v = g le palline arrivano insieme e con v < g vince chi lancia verso il l'alto. Se v > g invece vince chi lancia verso il basso. Sicuramente sbaglio ma mi sarebbe piaciuto provare a  formalizzare il ragionamento con la matematica ma oggi sicuramente non ce la faccio... mi si chiudono gli occhi dalla stanchezza....  :cry:

    Poco male tanto sarà sbagliato sicuramente!  :oops:

  4. Alvermag
    22/02/2016 at 20:54

    Diavolo Enzo, hai deciso di fare l'imbonitore?

    Venite siori, venite c'è posto, più siamo più ci divertiamo ....  A proposito di fiere paesane, mi è venuto in mente che la scorsa estate capitai in una di queste in un paesino dell'Abruzzo.

    Si trattava di una sorta di circo, molto alla buona, il cui cerimoniere presentava allo stupito pubblico esotici animali trattandoli come specie aliene.

    Ad un dato momento introdusse sul palco una malcapitata iguana dal colore verdastro.  A precisa domanda rispose che il colore era dovuto alla ... clorofilla!

    PEPPE, DOVE SEI!!!!!?????  SALVACI TU!!!!

  5. silvano
    22/02/2016 at 21:03

    :wink:

    nel vuoto ha ragione Alwermag , con l'aria ha ragione Alexander , ma a prescindere se v sia ...maggiore o minore di g

  7. Daniela
    22/02/2016 at 23:14

    Ho fatto una passeggiata nel bosco in cui si è addormentata la Fisica e ho raccolto alcune informazioni, vediamo se le ho comprese...

    Papallo rosso:

    V=Vo-gT  velocità alla quale viaggia la pallina rossa lanciata verso l'alto con velocità iniziale V0  (g=costante gravitazionale, T=tempo), gT è preceduta dal segno meno perché diretta in senso opposto alla terra

    finché V0>gT la pallina continua a salire

    quando V0=gT la pallina ha raggiunto la massima altezza, dopodiché comincia la discesa

    S=VoT-1/2gT^2  spostamento della pallina

    Sm=VoTm-1/2gTm^2  altezza massima raggiunta dalla pallina (T=Tm)

    S=VoT-1/2gT^2=T(Vo-1/2gT)=0  spostamento complessivo percorso dalla pallina quando avrà toccato terra

    Vo-1/2gTc=0   quindi Tc=2Vo/g   durata complessiva del moto

    Per calcolare la velocità finale con cui la pallina arriva al suolo, dobbiamo sostituire Tc  in V=Vo-gT ovvero Vf=V0-gTc=V0-g 2Vo/g=-V0

    quindi Vf=-Vo

    qualunque sia la velocità con cui la pallina viene lanciata in alto, la velocità con cui tocca terra è uguale a quella iniziale (con segno meno perché in senso opposto).

    Papallo blu:

    L'equazione del moto di un oggetto in caduta libera è V=V0+gT

    quindi la velocità finale Vf sarà data dalla somma della velocità iniziale con cui è stata lanciata + l'accelerazione gravitazionale moltiplicata per il tempo.

    Per quanto breve sia la caduta, se non nulla, Vf della pallina blu sarà sempre maggiore di Vf della pallina rossa, a parità di V0. 

    Quindi il blu vince sempre.

    (spero...)

     

  8. Arturo
    23/02/2016 at 00:00

    Ciao,

    lanciare verticalmente verso il basso o verso l'alto un oggetto da una stessa altezza e imprimendogli una stessa velocita' iniziale, non fa differenza ai fini della velocita' con cui l'oggetto arrivera' al suolo. Questa sara' pari , in entrambi i casi , a sqrt(v^2+2hg), dove h e' l'altezza da cui l'oggetto viene lanciato. Il motivo di cio' lo ha gia' spiegato Alvy. Naturalmente, non essendo stato detto qualcosa in contrario, ho ipotizzato anche io trascurabile la resistenza del mezzo.

  9. Arturo
    23/02/2016 at 00:09

    Dimenticavo di aggiungere che quello che cambia, tra lancio verso l'alto e lancio verso il basso , e' il tempo complessivo  di caduta, minore nel secondo caso. Ma, come precisato nel testo, in questo caso interessa solo la velocita' con cui l'oggetto arriva al suolo.

  10. Vincenzo Zappalà
    23/02/2016 at 05:15

    cari tutti,

    molto bene, molto bene... le risposte arrivano.

    I frequentatori di Papalla sanno che su questo bellissimo pianeta non c'è aria né attriti... e quindi...

    Alla bella addormentata nel bosco, faccio presente che in questo caso lanciamo da una certa altezza dal suolo: il discorso sulle velocità uguali e contrarie dolo la salita e la discesa non avviene al suolo, ma a livello piattaforma. Quindi.... :wink:

  11. Daniela
    23/02/2016 at 06:56

    ...quindi Vf=-Vo per la pallina rossa  vale a livello della piattaforma (non del suolo), da questo punto in poi le palline viaggiano alla stessa velocità V=Vo+gT e arrivano al suolo con la stessa Vf...

     

  12. Alexander
    23/02/2016 at 07:29

    Sisi me ne ero convinto anche io menere ci pensavo questa notte...

  13. michele
    23/02/2016 at 08:04

    Non vi sono forze esterne e quindi si conserva l'energia meccanica: Ec1+Ep1 = Ec2 + Ep2 ossia Ec2 = Ec1 +(Ep1-Ep2). La velocità iniziale interviene con il suo quadrato, il suo verso è ininfluente.

  14. Vincenzo Zappalà
    23/02/2016 at 08:06

    eh sì, sapevo che c'era di mezzo papalscherzone...

    Però, vale anche la pena di pensare ai concorrenti meno esperti, come diceva giustamente Alvy... E ne può nascere un bel giochino matematico con qualche angolo di mezzo... Ma, forse, questo è compito dei papallicoli & co. :lol:  :lol:  :lol:

  15. PapalScherzone
    23/02/2016 at 09:03

    Caro PapalEnzo, io non c'entro niente... Papaniela ha fatto tutto da sola e ti confesso che, a volte, mi verrebbe voglia di metterla al posto di papalAtleta QUI, ma poi penso che la caratteristica di Papallicoli non è quella di sapere tutto alla perfezione, ma di mettersi alla prova senza avere paura di sbagliare, con lo scopo di acquisire nuove conoscenze (o rispolverare conoscenze nascoste in qualche cassettino della memoria), e la speranza di invogliare altri a seguire il loro esempio :wink:

  16. Mik
    23/02/2016 at 09:15

    D'accordo con Alvermag. Se lancio in su con velocità v quando ripassa alla stessa quota cadendo nel senso opposto ha velocità -v. Quindi, ai fini della gara, lanciare in su o in giù a parità del modulo della velocità impressa non dà vantaggi. Cambia solo il tempo al quale la palla arriva al suolo.

    A occhio il risultato sarebbe lo stesso anche in presenza di aria.

    Certo che questi papalli sanno divertirsi con poco!

  17. PapalScherzone
    23/02/2016 at 09:28

    Infatti, Mik... esattamente come quando ai ragazzi terricoli bastava un sasso per giocare a campana o qualche amico per un nascondino o un-due-tre-stella, invece di passare il tempo attaccati ai telefonini... :roll:

  18. Vincenzo Zappalà
    23/02/2016 at 09:37

    caro papalschezone,

    io non intendevo che tu avessi aiutato papaldaniela... intendevo che nel quiz c'era il solito trucchetto che a te piace tanto... Dany, l'aveva già praticamente risolto  e gli bastava pensare alla piattaforma... :wink:

  19. umberto
    23/02/2016 at 09:50

    non so se sbaglio, ma nel caso di direzioni qualsiasi (oblique, non verticali)non conta sempre l'energia totale? ossia nel calcolo dell'energia cinetica non compare il modulo della velocità?

    Per il rosso: (indico con Vr,f la velocità finale di R, Vb,f la velocità finale di B)

    E_{R,tot}=m_{R}\cdot g\cdot h +\frac{1}{2} m_{R}\cdot V_{R}^{2}=\frac{1}{2}\cdot m_{R}\cdot V_{R,f}^{2}

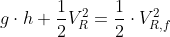    quindi g\cdot h +\frac{1}{2} V_{R}^{2}=\frac{1}{2}\cdot V_{R,f}^{2}   1)

    Per il blue:

    E_{B,tot}=m_{B}\cdot g\cdot h +\frac{1}{2} m_{B}\cdot V_{B}^{2}=\frac{1}{2}\cdot m_{B}\cdot V_{B,f}^{2}

    g\cdot h +\frac{1}{2} V_{B}^{2}=\frac{1}{2}\cdot V_{B,f}^{2}  2)

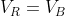    ma se: V_{R}=V_{B}   (sempre i moduli)

    dalla 1),2) si ha VR,f=Vb,F (sempre in modulo)

    in pratica se la componente verticale è più piccola, la velocità verticale finale anche, però sarà più grande quella finale  orizzontale essendo il modulo costante .

     

     

     

  20. Vincenzo Zappalà
    23/02/2016 at 10:20

    ci sono tanti papalscherzoni... :roll:  Mi piacerebbe che qualcuno usasse la legge oraria soltanto... così... tanto per gradire...

  21. Paolo
    23/02/2016 at 10:32

    Caro Enzo non so cosa dice Papalscherzone… però mi sembra di notare che come al solito ci sono modi diversi per affrontare il problema. :roll: 

    Quindi perché non provare a rispondere usando modi diversi?

    Tra i tanti ne ho scelto uno che non scomoda l'energia cinetica e di potenziale, ma solo le leggi legate al moto uniformemente accelerato.... 

    Parto dal fatto che l'accelerazione g è costante.

    Ciò significa che se all'altezza h la pallina ha una certa velocità V (come la pallina che tira verso il basso il Pappallo Blu) arriverà al suolo con una certa velocità finale VF.

    Lo stesso vale per la palla del Papallo Rosso... se quando torna all'altezza di h dal suo lancio verso l'alto arriva ad una velocità maggiore, minore o uguale a V, finirà al suolo con velocità maggiore uguale o identica a quella VF del papallo blu.

    Tanto vale concentrarsi su cosa succede alla palla del Papallo Rosso nel tratto che la porta verso l'alto per poi tornare all'altezza h con una certa velocità...

    Ciò che importa è proprio quanto vale quella velocità.

    La palla quando viaggia verso l'alto viene decelerata dalla forza di gravità, fino ad arrestarsi per poi ricadere verso il suolo. Quindi la sua velocità deve passare da V a zero.

    L'accelerazione indica proprio come varia la velocità nel tempo:

    a = (V2-V0)/(t2-t0)      nel caso della pallina rossa: a = (V-0)/t = V/t

    L'accelerazione è costante, per cui si può evitare di dover ragionare per dv/dt, ossia per intervalli piccolissimi.

    L'accelerazione in questo caso è quella di gravità, ossia g, solo che agisce nel verso opposto rispetto alla velocità V della pallina rossa, tanto che la frena fino ad arrestarne il moto:

    A questo punto è già chiaro che la pallina rossa torna all'altezza h con la stessa velocità con cui è partita, dato che l’accelerazione di gravità tanto toglie alla velocità V quando la pallina sale, tanto “restituisce” quando scende.

    Dopo che la pallina si è arrestata comincia nuovamente ad accelerare sempre a causa dell'accelerazione di gravità e dopo un certo intervallo di tempo torna all'altezza h.

    A questo punto meglio usare le leggi del moto.

    Quando la pallina rossa sale:  S1 = Vt - ½ gt²

    la velocità deve passare da V a zero, quindi l'accelerazione deve valere:

    g= (V-0)/t = V/t

    S = Vt - ½  (V/t)  t²

    S1 = ½ Vt

    Quando la pallina rossa scende

    S2 = ½ gt²

    La velocità deve passare da  zero a Vx (che è proprio il valore che si sta cercando).

    g= (Vx-0)/t = Vx/t

    S2 = ½ (Vx/t) t²

    S2 = ½ Vx t

    Ovviamente lo Spazio S è lo stesso dato che tanto sale la pallina, tanto scende per tornare ad h, quindi :

    S1 = S2

    ½ Vt = ½ Vx t

    Vt =Vx

    O anche, considerando direttamente andata e ritorno, essendo S1 un tratto  identico a S2,  lo spazio risultante è uguale a zero:

    S = Vt - ½ gt² - ½ gt²

    S= S1 – S2 =0

    0= Vt - ½  (V/t)t² - ½ (Vx/t)t²

    0 = Vt - ½  Vt - ½ Vxt

    0 = ½  Vt - ½ Vxt

    ½ Vxt = ½  Vt

    Vx =  V

    Dato che la pallina Rossa quando torna all'altezza h ha la stessa velocità V della pallina blu lanciata verso il basso, entrambe arrivano al suolo con la medesima velocità..... o almeno questo è quello che mi ha suggerito Papalscherzone, ma si sa sempre meglio non fidarsi.... :-P 

    Paolo

  22. Vincenzo Zappalà
    23/02/2016 at 10:49

    caro Paolino,

    e se il lancio avviene in una direzione qualsiasi, cosa succede alla velocità finale rispetto a quella iniziale?

  23. Paolo
    23/02/2016 at 11:16

    Ma così di botto, io scomporrei la velocità in due componenti una nella direzione di g e l'altra in direzione ad essa perpendicolare.. (Vx e Vy).

    Se le due componenti delle velocità di entrambe le palline sono uguali, non dovrebbe mutare il risultato finale, dato che quando le palline impattano il suolo, si dovrebbe ricomporre il vettore V, usando il teorema di Pitagora VF= √(Vx² + Vy²)…

    Ma dovrei ragionarci con calma… e potrei aver detto qualche strepitosa sciocchezza.. :roll:

    Paolo

  24. Vincenzo Zappalà
    23/02/2016 at 11:21

    le due palline hanno componenti diverse in x e y, dato che vengono lanciate a casaccio... ma...

  25. Paolo
    23/02/2016 at 11:33

    Ah ma voi terricoli siete incontentabili…

    Anche qui rispondo di botto…

    Uso il tempo, partendo dall’accelerazione di gravità:

    h = ½ g t²

    2h = g t²

    t = √(2h/g)

    nel medesimo tempo posso provare a vedere cosa succede alle due palline, in direzione di Vx e Vy....

    Paolo

  26. Daniela
    23/02/2016 at 11:47

    Una risposta di botto anche da parte mia...

    per caso dobbiamo considerare solo la componente verticale Vy del vettore V, il cui modulo è pari al modulo di V moltiplicato per il coseno dell'angolo adiacente (ovvero l'angolo compreso tra V e Vy)?

     

  27. Vincenzo Zappalà
    23/02/2016 at 11:50

    basta pensare ai cannoni, agli obici e ai mortai... :wink:

  28. Paolo
    23/02/2016 at 11:58

    Ma su Papalla la guerra non esiste,  nessuno pensa a quelle cose....  piuttosto che pensarci i papalli  raggiungono in un attimo la velocità di fuga...

    Paolo

  29. PapalScherzone
    23/02/2016 at 12:00

    Grande Paolo!!

    :mrgreen: :mrgreen:

  30. umberto
    23/02/2016 at 12:48

    scusa ma non credevo che fosse richiesta una dimostrazione prettamente cinematica, per me quella energetica era quella più semplice, comunque proverò a scriverla, se ancora é aperto il quiz

  31. umberto
    23/02/2016 at 14:42

    cominciamo con le componenti solo verticali;

    possiamo fare un sistema con le due leggi della velocità e dello spazio (parabola)

    Indichiamo con Vo la velocità iniziale , V quella finale

    V= V_{0}-gt

    t=\frac{V_{0}-V}{g}

    S=h + V_{0}t-\frac{1}{2}gt^{2}

    quando S=0

    0=h + V(V_{0}-V)/g -\frac{1}{2}g(V_{0}-V)^{2}/g^{2}

    0= 2hg +V_{0}^{2}-V^{2}

    V^{2}=2hg + V_{0}^{2}

    (questo è valido sia che Vo sia risolta verso il basso che verso l'alto, quindi non dipende se la pallina va in su o in giù) quindi V è sempre la stessa

    Consideriamo ora una velocità obliqua che formi un angolo \alpha con la piattaforma orizzontale:

    V_{y}^{2}=V_{0y}^{2}+ 2gh

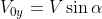
    ma V_{0y}=V\sin \alpha

    V_{y}^{2}=V^{2}\sin ^{2}\alpha +2gh

    V_{x}^{2}=V^{2}\cos ^{2}\alpha (la velocità orizzontale non viene alterata)

    V^{2}=V_{y}^{2}+V_{x}^{2}=V(\sin ^{^{2}}\alpha +\cos ^{2}\alpha ) + 2gh=V^{2}+2gh

    quindi la velocità finale non dipende nemmeno da \alpha

     

     

  33. Paolo
    23/02/2016 at 22:16

    Però io conosco un papallino che ha lanciato la sua palla Rossa e non è più tornata... mi dicono che il raggio del pianeta Papalla è simile a quello terrestre, ossia 6.370 km... anche g è uguale... chissà a quale velocità ha lanciato la pallina.... :roll:

    Paolo

  34. Daniela
    23/02/2016 at 23:30

    Se anche la massa di Papalla è uguale a quella della terra, la velocità di fuga sarà pari a 11,2 Km/sec, come è ben spiegato QUI

    Infatti l'energia totale della pallina (che deve conservarsi) è data dalla somma dell'energia cinetica e dell'energia potenziale

    E=Ec+Ep= 1/2mv^2-gMm/r=0

    m=massa della pallina (è ininfluente e lo sarebbe anche se fosse un oggetto molto più grande, per esempio un razzo)

    svolgendo i calcoli, Vf=(2gM/r)^1/2

    sostituendo i valori di M,g,r della Terra, si ottiene 11,2 Km/sec

    Forte questo papallino... chissà quanti biscotti avrà mangiato  :roll:

     

     

     

  35. Arturo
    24/02/2016 at 01:42

    legge oraria del moto uniformemente accelerato:

    \inline s(t)=so+vo*t+\frac{1}{2}*a*t^2       (1)

    v(t)=vo+a*t        (2)

    applichiamola al caso dell'oggetto che viene lanciato verso l'alto:

    s(t)-so=vo*t-\frac{1}{2}*g*t^2      (1 a)

    v(t)=vo-g*t         (2 a)

    se indico con t l'istante di tempo in cui l'oggetto raggiunge la massima altezza e si ferma in aria prima di ricadere, allora v(t)=0 e quindi dalla (2 a) ottengo

    t=\frac{vo}{g}

    sostituisco l'espressione appena trovata per t nella (1 a) ottenendo:

    s(t)-so=\frac{1}{2}\frac{vo^2}{g}       (3)

    ma s(t)-so altro non è che l'altezza h , rispetto alla quota iniziale H, raggiunta dall'oggetto lanciato verso l'alto che, quindi, ricadendo verso il suolo vi arrivera' con una velocita' finale dovuta ad una altezza di caduta pari a H + h. Riapplico le (1) e (2) per trovare l'espressione della velocità finale, sapendo che stavolta il corpo comincia a cadere con velocita' iniziale nulla ma da una altezza H+h rispetto al suolo:

    dalla (1):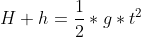    H+h=\frac{1}{2}*g*t^2

    dalla (2):   vf=g*t

    dalla (2) mi ricavo l'espressione di t :

    t=\frac{vf}{g}

    e la vado a sostituire nella (1):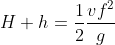  H+h=\frac{1}{2}\frac{vf^2}{g}

    da cui , tenendo con che dalla (3)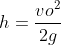  h=\frac{vo^2}{2g} , esplicitando rispetto a vf ottengo:

    vf^2=2*H*g+vo^2

    ed estraendo la radice quadrata:

    vf=\sqrt(2*H*g+vo^2) velocità finale nel caso in cui l'oggetto venga lanciato in aria da una altezza H con velocità vo.

    Passiamo ora al caso dell'oggetto lanciato verso il basso, piu' semplice perche' non ho una fase preliminare di salita come nel primo caso. Quindi ora applico le (1) e (2) e ottengo:

    s(t)-so=vo*t+\frac{1}{2}g*t^2

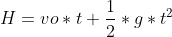    cioe' H=vo*t+\frac{1}{2}*g*t^2        (1 b)

    v(t)=vo+g*t

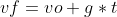    cioè vf=vo+g*t      (2 b)

    dalle suddette (1 b) e (2 b) ,ricavando t dalla seconda e andando a sostituirlo nella prima, ottengo dopo qualche passaggio:

    H=\frac{vf^2}{2g}-\frac{vo^2}{2g}

    da cui, esplicitando rispetto a vf, ottengo:

    vf=\sqrt(2*H*g+vo^2)  velocità finale nel caso dell'oggetto lanciato verso il basso da una altezza H con velocità vo.

    Come si vede, dunque, le espressioni della velocità finali al suolo nei due casi  coincidono .

     

     

  36. Arturo
    24/02/2016 at 01:51

    ok, solo dopo aver risposto mi sono accorto della seconda pagina di risposte.. :-D

  37. Vincenzo Zappalà
    24/02/2016 at 05:28

    insomma... io pongo un quiz semplice semplice e si scatena la corsa alla complessità... :mrgreen: Comincio a pensare che questo sia l'unico circolo di ricerca in cui si otterrà la "grande unificazione"8-O.

    Grazie ragazzi, mi aiutate moltissimo con i vostri commenti e le vostre aggiunte a rendere sempre più stimolante qualsiasi quiz anche se ridicolo... E in più quel tocco di ironia che ci vuole sempre (un omaggio a Eco...).

    Il massimo è poi quando ci si complimenta con se stessi!!!! :mrgreen:  :mrgreen:

    Troppo forti i papallicoli...

    Dai adesso vi lascio un po' in pace  vado avanti con la DR.

  38. PapalScherzone
    27/02/2016 at 21:23

    Cara Dany,

    ho letto la tua risposta alla domanda di Paolo e, pur essendo formalmente corretta (a parte l'uso della g minuscola anziché maiuscola per indicare la costante di gravitazione universale), credo che Paolo avesse in mente qualcos'altro... non a caso ha parlato di g e non di G, e poi ha fatto riferimento solo al raggio del pianeta e non alla massa...

    Ci ho pensato e ripensato e secondo me (mumble... mumble...) è possibile calcolare la velocità di fuga utilizzando soltanto raggio del pianeta e accelerazione gravitazionale, guarda qui:

    F=\frac{GMm}{r^{2}}       ma è vero anche che F=ma

    e poiché a=g , arriviamo a

    {GMm}/{r^{2}}=mg  e semplificando m da entrambi i membri  GM/r^{2}=g

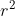    da cui M=gr^{2}/G

    inserendo questo valore di M nella formula della velocità di fuga:

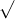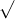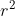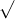    Vf=\sqrt{}2G/r *M = \sqrt{}2G/r * gr^{2}/G = \sqrt{}2gr

    quindi, andando a sostituire i valori di g e r terrestri:

    Vf=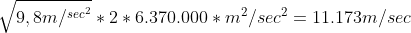 \sqrt{9,8m/^{sec^{2}}}*2*6.370.000*m^{2}/sec^{2}=11.173 m/sec

    ovvero circa 11,2 Km/sec

    Ti torna, Paolino?!

    :-P

  39. Paolo
    27/02/2016 at 21:41

    Ma tu guarda Papalscherzone, quasi, quasi, mi ha letto nel pensiero... 8-O .

    Si papalchiacchierava se era possibile determinare la velocità di fuga usando solo il valore dell'accelerazione di gravità al suolo g ed il raggio di Papalla.

    Prima di lanciare la pallina, questa è ferma, ossia Vo= 0

    L'energia cinetica della pallina ferma è: Ec=½mVo²=0

    La sua energia di potenziale è: Ep = -GMmr

    Per r si intende la distanza tra la pallina ferma e il centro del Pianeta Papalla (quindi comprende anche l'altezza h dal suolo).

    L'Energia totale quando la pallina è ferma vale: Etot= Ec +Ep

    Quando la pallina viene lanciata la sua Energia cinetica cambia (d'altronde bisogna utilizzare una certa energia per accelerare la pallina :roll: ): Ec=½ mV²

    Questa velocità deve essere sufficiente per sfuggire alla gravità, per cui la chiamo Vf.

    Ovviamente cambia anche l'Energia Totale :

    Etot = ½ m Vf² - GMm/r

    Pur non conoscendo la massa M del Pianeta Papalla, si conosce il valore dell'accelerazione di gravità al suolo di Papalla, ossia g.

    La Forza di attrazione gravitazionale vale: F = GMm/r²

    ma.... F = m a …..... e l'accelerazione è quella di gravità, ossia g:

    g = F/m = GMm/mr²

    g= GM/r²

    quindi: GM/r = gr

    Etot = ½ m Vf² - GMm/r

    Etot = ½ m Vf² – m gr

    L'Energia cinetica della pallina è destinata ad esaurirsi quando la sua distanza da Papalla si avvicina a infinito, mentre la negativa Energia di potenziale continua a crescere fino ad avvicinarsi a zero (parte da valori negativi, per cui più si avvicina a zero e più cresce).

    Quindi in quell'ipotetico momento l'Energia Totale diventa uguale a zero:  Etot=Ec+Ep=0

    L'Energia totale della pallina deve conservarsi (nel viaggio c'è solo l'Energia cinetica che diminuisce e quella di potenziale che aumenta), quindi l'Energia Totale deve essere la stessa di quando la pallina è stata lanciata:

    Etot = ½ m Vf² – m gr =0

    ½ m Vf² – m gr =0

    ½ m Vf² = m gr

    Vf² = 2gr

    Vf = √2gr

    Vf = √2 (9,82 m/sec² ) (6 370 000 metri)

    Vf = 11 185 metri/sec = 11,185 Km/sec

    La pallina Rossa per non tornare più deve esser lanciata ad una velocità di 11,185Km/sec.... questa è la sua velocità di fuga da Papalla...

    Più o meno torna, cambia solo di poco il metodo usato e l'approssimazione di g... ma se Papalscherzone o Papalmatematico travestito :?:

    Paolo

  40. PapalScherzone
    27/02/2016 at 21:57

    Ma tu guarda... per una volta che risolvo un quiz, il mio Paolino pensa che non sia io ma PapalMatematico travestito  :roll:

    Ti va ti fare qualche giro intorno a Papallone per verificare se esiste forza centrifuga??

    :mrgreen:   :-P

  41. Paolo
    27/02/2016 at 22:57

    Solo dopo aver convinto Papalcontadino a spostare il letame ed essermi assicurato che non gironzoli intorno alla centripeta.... ma tanto lo so che escogiteresti qualche altro scherzone... 8-O  8-O 

  42. PapalScherzone
    27/02/2016 at 23:16

    :mrgreen:  :-P  :mrgreen:

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.