Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Finora non abbiamo parlato di unità dell’asse del tempo nella Fig. 1 (l’abbiamo riportata anche in questo articolo, chiamandola Fig. 2).

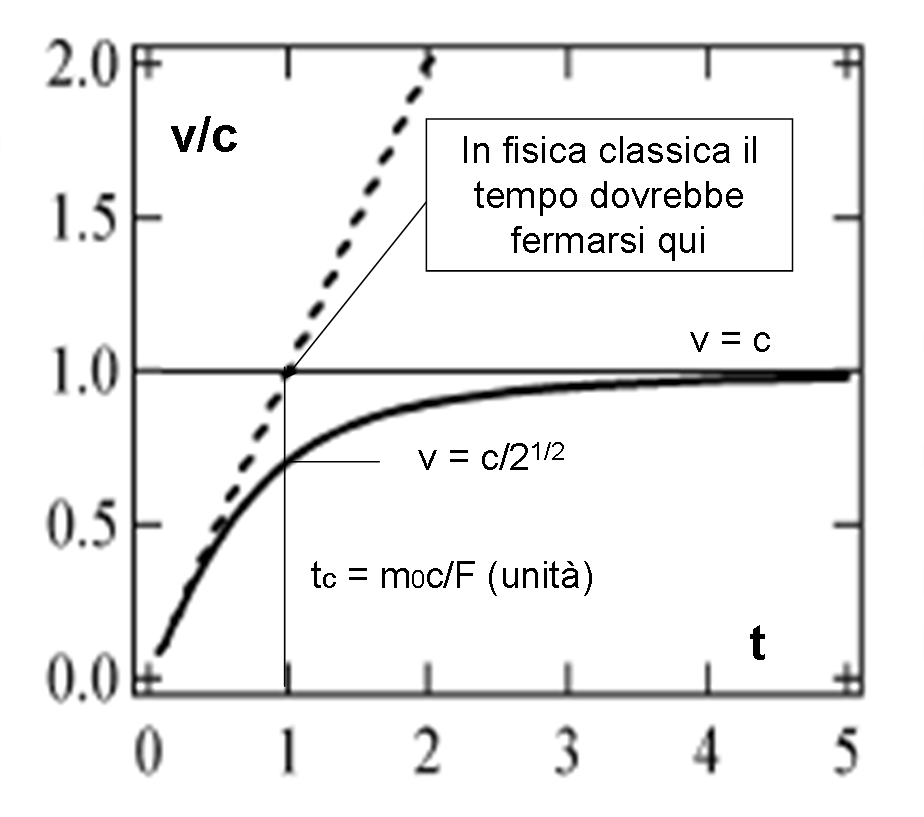
Non ve ne era bisogno, ma tanto vale introdurla. Essa altro non è che quella che corrisponde al tempo:

t_U = m₀c/F     (il tempo “critico” della volta scorsa)

Per questo valore il denominatore della (4) diventa uguale a √2 m₀. A ciò corrisponde una velocità pari a:

v(t₀) = (Fm₀c/Fm₀√2) = c/√2

E’ facile notare che per valori molto inferiori a t = 1, la curva tratteggiata (classica) è praticamente coincidente con quella relativistica. La (4) si riduce praticamente alla (2).

In altre parole, data una certa massa, non si può fare agire per troppo tempo una certa forza, se no la fisica classica perde di significato e la velocità assume un andamento assurdo. Invece, ciò è del tutto possibile con la nuova definizione di velocità. In realtà, la forza continua ad agire, ma il suo contributo non si riversa tutto sulla velocità. Se non si riversa sulla velocità vuol dire che cambia il modo di farla variare, ossia l’accelerazione (quella che comanda la variazione della velocità) comincia a perdere “colpi”.

Notiamo, infatti, che la pendenza istantanea della curva velocità (ossia l’accelerazione) non rimane assolutamente costante, anche se la forza lo è. E questo è un qualcosa che farebbe sobbalzare il povero Newton. In particolare, l’accelerazione decresce all’aumentare della velocità. Ciò deriva dal fatto che mentre la velocità aumenta, aumenta anche la massa della particella (m₀γ). Teoricamente per velocità prossima a quella della luce, l’accelerazione tende a zero.

Potremmo, ad occhio per adesso, determinare tre zone nella curva: (a) quella iniziale rettilinea in cui l’applicazione della forza causa un aumento lineare dell’accelerazione. La massa praticamente non cambia. (b) La seconda che può essere chiamata relativistica, in cui la forza fa aumentare sia la velocità, ma in modo meno rapido, che la massa del corpo, in grado, perciò, di controbattere sempre più all’accelerazione: l’inerzia aumenta. Ovviamente, per cercare di raggiungere una certa velocità è necessario fare agire la forza per tempi molto lunghi. (c) La terza zona  (ultra relativistica) torna a essere quasi rettilinea, ma in direzione… orizzontale. Quasi tutta l’azione della forza si traduce in un aumento della massa e la velocità resta praticamente costante, essendo ormai prossima a quella della luce.

Possiamo dire tranquillamente che la velocità di qualunque corpo materiale che abbia una massa inerziale a riposo diversa da zero non può mai raggiungere valori uguali o superiori a c.

Infatti, a mano a mano che aumenta la velocità del corpo, a causa dell'aumento della massa, l'accelerazione diminuisce e la velocità cresce più lentamente avvicinandosi sempre più al valore limite v = c, che viene raggiunto solo nel limite di un tempo infinito.

Quanta fisica rivoluzionaria c’è dentro a queste semplici riflessioni… Abbiamo una massa inerziale che aumenta e che costringe, a parità di forza, a diminuire l’accelerazione e di conseguenza a far crescere la velocità sempre più lentamente.

All’interno di questa frase è già presente il concetto che  evidenzia l’impossibilità di raggiungere velocità troppo alte con oggetti di massa “normale”, dato che bisognerebbe fornire un’energia incredibilmente alta. Cosa, questa, che vedremo meglio in seguito… In ogni modo, già capiamo che, per raggiungere una velocità uguale a quella della luce, la massa dovrebbe diventare infinita (quanta fatica dovrebbe fare la forza…).

Ma, in realtà, esiste qualcosa che va alla velocità della luce… anzi che può esistere solo muovendosi a quella velocità. Lo conosciamo molto bene: il fotone. Ma allora il fotone ha sempre massa infinita? No, nemmeno lui può arrivare a tanto e ce lo dice un concetto matematico molto semplice. E’ vero che il denominatore della sua massa relativistica tende a zero, ma fa lo stesso anche il suo numeratore, dato che la massa a riposo è uguale a zero. E zero su zero è una forma indeterminata. Non per niente, il fotone ha un’energia finita e tra poco vedremo che massa ed energia sono praticamente la stessa cosa…

Per riuscire, comunque, a portare la velocità a livelli molto alti è necessario avere a che fare con particelle molto piccole. Per loro è decisamente più facile raggiungere accelerazioni elevatissime attraverso speciali strumentazioni, che ben conosciamo: gli acceleratori di particelle.

Possiamo senz’altro concludere che il mondo della relatività speciale è proprio quello degli elettroni, dei protoni e dei loro fratellini.

Vale, però anche il contrario… Poter imprimere accelerazioni così grandi a particelle elusive ma concrete, permette di verificare la perfetta validità della (4) anche per velocità prossime a quella della luce. La teoria ha dovuto aspettare proprio loro per mostrare la sua immensa portata.

Particelle insignificanti per l’Universo? O addirittura del tutto ipotetiche e mai rilevate? Assolutamente no. Anzi, proprio i mattoni fondamentali di tutto ciò che esiste. Vi sembra poco?

La teoria della RR è una vera teoria scientifica che ha fornito tutte le possibilità alla mente e alla tecnologia umana per potere essere confermata osservativamente. Tanto di cappello, signor Einstein!

No, cari amici, la dinamica relativistica non è difficile, ma senza averne una conoscenza sufficiente (anche se non specialistica) è ASSURDO disquisire su relatività generale, curvatura dello spaziotempo, densità critica dell’Universo, buchi neri, radiazione di Hawking, energia negativa, wormhole, singolarità, onde gravitazionali e mille altri argomenti ai confini della Scienza attuale.

Ricordiamoci (e un giorno -forse- riusciremo a parlarne diffusamente) che proprio dalla formula più importante della RR (non quella più mediatica) è nato il mare di Dirac e il concetto di energia negativa. La fantasia può anche essere libera di volare, ma se mancano le basi “fondamentali”, diventa pura fantascienza, poco divertente e ancora meno utile, sia per chi la scatena sia per chi la subisce. Tutti voi sapete benissimo a chi e a cosa mi riferisco…

Dirac poteva anche permettersi di immaginare un’energia negativa, così come Planck poteva anche pensare all’energia regalata a “pacchetti” (e non ne era nemmeno troppo convinto). Entrambi conoscevano bene ciò che era stato raggiunto dalla Scienza fino a quel punto. La loro fantasia poteva e doveva volare. Ma chi non conosce nemmeno le leggi di Newton, o giù di lì, può permettersi di prospettare teorie alternative a quelle su cui veri scienziati hanno trascorso anni e anni di dura riflessione e di studio? No, non lo posso accettare e quel novello “genio” dovrebbe essere zittito immediatamente. Vi sono mille modi per sfogare la propria fantasia e quel felice e puro mondo di Papalla ce lo insegna.

Scusate questi sfoghi, ma li reputo importantissimi soprattutto per i giovani. Quando ho letto (poco tempo fa) che un maturando vorrebbe scrivere una tesina sul ponte di Einstein-Rosen e sulle formule applicate ai wormhole, mi sono venuti i brividi. La ragione ultima è solo mediatica, ossia la visione di un recente film di fantascienza (sbaglia perfino il nome del ponte, inserendo quello del fantomatico pianeta del film), ma la richiesta apre un baratro terribile sull’insegnamento scolastico e sulla facilità di trovare di tutto e di più sulla rete, senza nessun segnale di pericolo.

Ci si accorge subito che, ovviamente, quel ragazzo non ha la più pallida idea della RR e della RG, tranne poche frasi fatte e vaghi concetti confusi. E’ il momento di bloccarlo, di fargli capire che certi argomenti non si inventano dall’oggi al domani, che hanno dietro costruzioni logiche, fisiche e matematiche enormi. Comprensibili sì, ma con tanta dedizione e attenzione. Soprattutto, bisognerebbe dirgli che anche nel mondo virtuale e del “copia e incolla” di oggi è necessario studiare!

E, invece, lo si incoraggia anche, facendogli capire, tra le righe, che chiunque potrebbe, in fondo, disquisire di certe faccende scientifiche. No, non voglio considerare la Scienza come  “cosa” da elite dei cervelli. Proprio il contrario. Vorrei solo far capire che i castelli hanno bisogno di fondamenta se no crollano al primo alito di vento. E, poi, se non altro, per un minimo di rispetto verso i grandi filosofi greci, Galileo, Giordano Bruno, Newton, i fisici dell’ottocento e del primo novecento, e -non certo ultimo- il nostro Einstein.

Concludo subito questo intermezzo, che ho inserito volontariamente all’interno della dinamica relativistica. Solo chi ha sentito il bisogno di entrare senza timore o falsa arroganza nella realtà einsteniana è in grado di capire appieno le motivazioni di questi sfoghi e di aiutarmi a riportare i giovani sulla giusta strada della conoscenza. Stiamo lontani e - nel caso- osteggiamo con forza  chi disquisisce, senza alcuna base solida, di fantasie scientifiche personali e si convince (ed è anche incoraggiato a farlo) di fare Scienza!

Forza costante, accelerazione che perde i colpi, velocità timorosa di giungere a livelli troppo alti, inerzia al moto che cresce con la velocità, energia che si affaccia in modo innovativo…  e tutto ciò solo imponendo la costanza della velocità della luce o poco di più. Questa è fantasia geniale!

Va bene, è giunta l’ora di affrontare il punto più famoso della relatività. Un punto famoso che diventa quasi ovvio proseguendo con logica e conoscenza. La vera grandezza di Einstein è che LUI lo aveva già previsto perfettamente, ben prima di arrivarci con le formule.