Dinamica relativistica. 3: Massa ed energia 2 **

05/03/16

Dinamica relativistica. 3: Massa ed energia 2 **

Categorie: Relatività Tags: Scritto da: Vincenzo Zappalà Commenti:9

Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Qualcuno potrebbe commentare: “Abbiamo scritto la nuova versione dell’energia cinetica e il risultato ci ha emozionato e ci ha fatto perdere di vista la realtà…  La formula ricavata non ha alcuna somiglianza con quella classica. Eppure, per basse velocità dovrebbe coincidere con lei…”. Questo qualcuno avrebbe ragione. Per noi è un vero piacere dimostrargli che in effetti è proprio così. Un piacere, anche perché sfrutteremo di nuovo gli sviluppi in serie! Anzi, proprio uno che avevamo risolto come esercizio (QUI) … Chi vuole provare, può partire da qui e risolvere il problema da solo...

Consideriamo la funzione:

(1 + x)α      …. (4)

Il suo sviluppo in serie risulta:

(1 + x)α = 1 + αx + (α – 1)x2/2! + …

E non c’è nemmeno bisogno di andare oltre. Anzi, possiamo già fermarci ai primi due termini. Se x << 1, basta e avanza…

Non ci credete? Basta provare…

Scegliamo

α = ½

e

x = 0.01

Facendo i conti:

(1 + 0.01)½  = 1.00498

1 + 0.01/2 =  1.00500

La differenza è di un 2 sulla quinta decimale.

Prendiamo, adesso:

x = 0.0001

(1 + 0.0001)½  = 1.000049999

1 + 0.0001/2 = 1.000050000

La differenza è diventata solo un 1 sulla nona cifra decimale.

Immaginiamo, per un momento (ma non solo…), che la nostra x sia uguale a (v/c)2

x = 0.0001

vorrebbe dire

x = v2/c2 = 0.0001

ossia (circa):

v = 3000 km/sec

Una velocità niente male… possiamo accontentarci! Sicuramente Newton lavorava con velocità più basse.

Riprendiamo la nostra funzione e poniamo allora:

x = - (v/c)2

e

α = - 1/2

Essa diventa

((1 - (v/c)2))-1/2 = 1/(1- (v/c)2)1/2

Questa funzione la conosciamo molto bene! Non è altro che il fattore γ !

Ma, allora, possiamo sviluppare in serie il fattore γ fermandoci al secondo termine:

γ = 1 + (v/c)2/2

e poi inserirlo nella formula dell’energia cinetica relativistica:

K = c2· m0 γ - c2· m0

Si ha:

K = m0c2 (1 + v2/c2)/2 – m0c2 = ½ m0v2

Che è proprio l’energia cinetica newtoniana!

Eh sì, Einstein ha sempre ragione!

Articoli correlati

9 commenti

  1. Umberto
    05/03/2016 at 10:05

    Grazie al lavoro preparatorio che hai svolto in precedenza con quiz ed esercizi stanno diventando semplici anche queste cose che sembravano irraggiungibili.

    Sono molto soddisfatto.

  2. Vincenzo Zappalà
    05/03/2016 at 10:15

    sono molto contento anch'io, caro Umberto!!!!

  3. Mik
    07/03/2016 at 22:50

    Quest'articolo risponde perfettamente alla domanda che ti ponevo, grazie!

    Ho provato ad aggiungere qualche termine alla serie tanto per vedere cosa succede.

    Considerando lo sviluppo fino alla terza potenza di x:

    (1+x)^\alpha = 1 + \alpha x + \frac{\alpha(\alpha-1)}{2!}x^2 + \frac{\alpha(\alpha-1)(\alpha-2)}{3!}x^3 + \dots

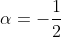    con \alpha=-\frac{1}{2}  lo sviluppo diventa (se non ho fatto errori):

    (1+x)^{-\frac{1}{2}}=1-\frac{1}{2}x+\frac{3}{8}x^2-\frac{15}{48}x^3+\dots

    sostituendo x=-\left(\frac{v}{c}\right)^2 si dovrebbe ottenere:

    \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=1+\frac{1}{2}\frac{v^2}{c^2}+\frac{3}{8}\frac{v^4}{c^4}+\frac{15}{48}\frac{v^6}{c^6}+\dots

    Sostituendo nella espressione della energia cinetica e svolgendo i calcoli si arriva a:

    K=c^2m_0\gamma-c^2m_0 =\frac{1}{2}m_0v^2+\frac{3}{8}\frac{m_0}{c^2}v^4+\frac{15}{48}\frac{m_0}{c^4}v^6+\dots

    Quindi i termini ulteriori sono effettivamente molto piccoli per piccole velocità (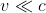v \ll c) ma quando la velocità comincia a crescere iniziano a diventare rilevanti, e anche rapidamente viste le potenze in gioco. Se ne interpreto bene il significato, a velocità relativistiche il lavoro fatto dalla forza F di partenza finisce quasi completamente nei termini di ordine superiore mentre il termine che rappresenta l'energia cinetica "classica" aumenta solo di poco.

     

  4. Vincenzo Zappalà
    08/03/2016 at 06:06

    bravo Mik... il concetto è proprio quello! :wink:

  5. Paolo
    12/03/2016 at 15:05

    Caro Enzo questo articolo mi ha fatto a tornare alla mente questo quiz... :-D

    Paolo

  8. Paolo
    12/03/2016 at 15:13

    Quello che mi ero dimenticato di linkare: una serie molto energetica..

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.