QUIZ: un animale per ciascun pianeta *

19/03/16

QUIZ: un animale per ciascun pianeta *

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:8

Consideriamo tre corpi celesti del nostro Sistema Solare: L’asteroide Eros, il pianeta Marte e il pianeta Giove. Per semplificare i calcoli, possiamo assumere che siano tutti e tra perfettamente sferici e che il raggio di Eros sia pari a 10 km; quello di Marte a 3000 km e quello di Giove a 70 000 km.

A questo punto, prendiamo tre corde molto robuste e circondiamo perfettamente i tre oggetti celesti lungo il loro equatore. Fatto? Perfetto… Adesso, tagliamo le tre corde e aggiungiamo un metro di corda a ciascuna di loro e riannodiamo il tutto. Rimettiamo le tre corde così allungate attorno ai tre pianeti. Ovviamente, le tre nuove “cinture” staranno un po’ larghe rispetto a prima.

Davanti a noi abbiamo una bella sfilza di animali. Esattamente: un virus della varicella, una pulce, un lombrico, un topolino, un gatto e un elefante.

Potreste indicarmi, per ciascun corpo celeste, l’animale più grosso, tra quelli precedenti, che riuscirebbe a passare tra il corpo e la corda che lo avvolge?

Eros:   ? 

Marte:   ?

Giove:   ?

zoo

Articoli correlati

8 commenti

  1. Vincenzo Zappalà
    20/03/2016 at 15:47

    possibile che nessuno abbia voglia di rispondere??? è facilissimo....

  2. silvano
    20/03/2016 at 21:04

    In tutti e tre i casi il diametro risulta maggiorato di 1 m/6,28 e quindi l'animale piu' grosso che puo' passare e' il gatto

  3. Paolo
    20/03/2016 at 21:49

    Scusa Silvano posso chiederti due cose?

    La prima è: puoi spiegare meglio come sei giunto a quella conclusione?

    La seconda: il rapporto che hai indicato è riferito al diametro o al raggio?

    Paolo

  4. silvano
    20/03/2016 at 22:17

    non riesco a digitare 2 p greca e quindi scrivo 6,28

    6,28 x R1 = 10.000 metri

    6,28 x R2 = 10.001 metri

    quindi R2-R1 = 1 metro / 6,28 = 0,159 metri = 15,9 centimetri

     

  5. Arturo Lorenzo
    20/03/2016 at 23:17

    Facile ma curioso. A prima vista e senza pensarci, uno direbbe a cuor leggero che lo spazio tra il pianeta e la corda che lo avvolge aumenta all'aumentare del raggio del pianeta. Ma pensandoci su e facendo due conti risulta invece che , indicando con R1 il raggio (in metri) del generico pianeta, con R2 il raggio  della circonferenza di corda che avvolge lo stesso generico pianeta, con (R2-R1) lo spazio  tra la corda che avvolge il generico pianeta e il generico pianeta stesso:

    L1 = circonferenza del generico pianeta =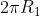 2\pi R_{1}

    L2 = circonferenza della corda che avvolge lo stesso pianeta = L1+1 = 2\pi R_{1}+1

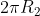
    ma L2 = 2\pi R_{2}

    quindi, dalle ultime due relazioni:

    2\pi R_{1}+1=2\pi R_{2}

    dividendo primo e secondo membro per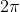 2\pi ed esplicitando rispetto a (R_{2}-R_{1}) ottengo:

    (R_{2}-R_{1})=\frac{1}{2\pi}

    da notare che ho parlato di generico pianeta e non ho fatto riferimento ad alcun valore numerico dei rispettivi raggi. Cioè, la suddetta relazione ha carattere generale, a prescindere dal pianeta. Lo spazio disponibile sarà sempre 0,16 m circa, sufficiente quindi per far passare il gatto.

     

  7. Daniela
    21/03/2016 at 22:53

    Infatti, facendo i calcoli:

    r1                       C1=2\pir              C2=C1+1           r2=C2/2\pi               r2-r1

    10.000             62.800               62.801               10.000,16                0,16

    3.000.000     18.840.000        18.840.001       3.000.000,16         0,16

    70.000.000   439.600.000     439.600.001    70.000.000,16       0,16

    Quindi circa 16 centimetri, sufficienti per un bel micione!

     

  8. Vincenzo Zappalà
    22/03/2016 at 06:45

    eh sì, è un classico... ma la prima impressione sembrerebbe dover dare un risultato ben diverso. E invece, la differenza è indipendente dal raggio...

    Conclusione? Nei futuri viaggi spaziali basta portarsi dietro un metro di corda e un bel micione!!!! :mrgreen:

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.