Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Analizziamo nuovamente, con particolare attenzione, un caso semplicissimo: l’urto frontale anelastico, lo stesso attraverso cui avevamo trovato che M₀ > 2m₀ (QUI).

Nel sistema di riferimento S’, due corpi A e B, di pari massa a riposo m_0, viaggiano uno contro l’altro con velocità u’₀ come mostrato in Fig. 1.

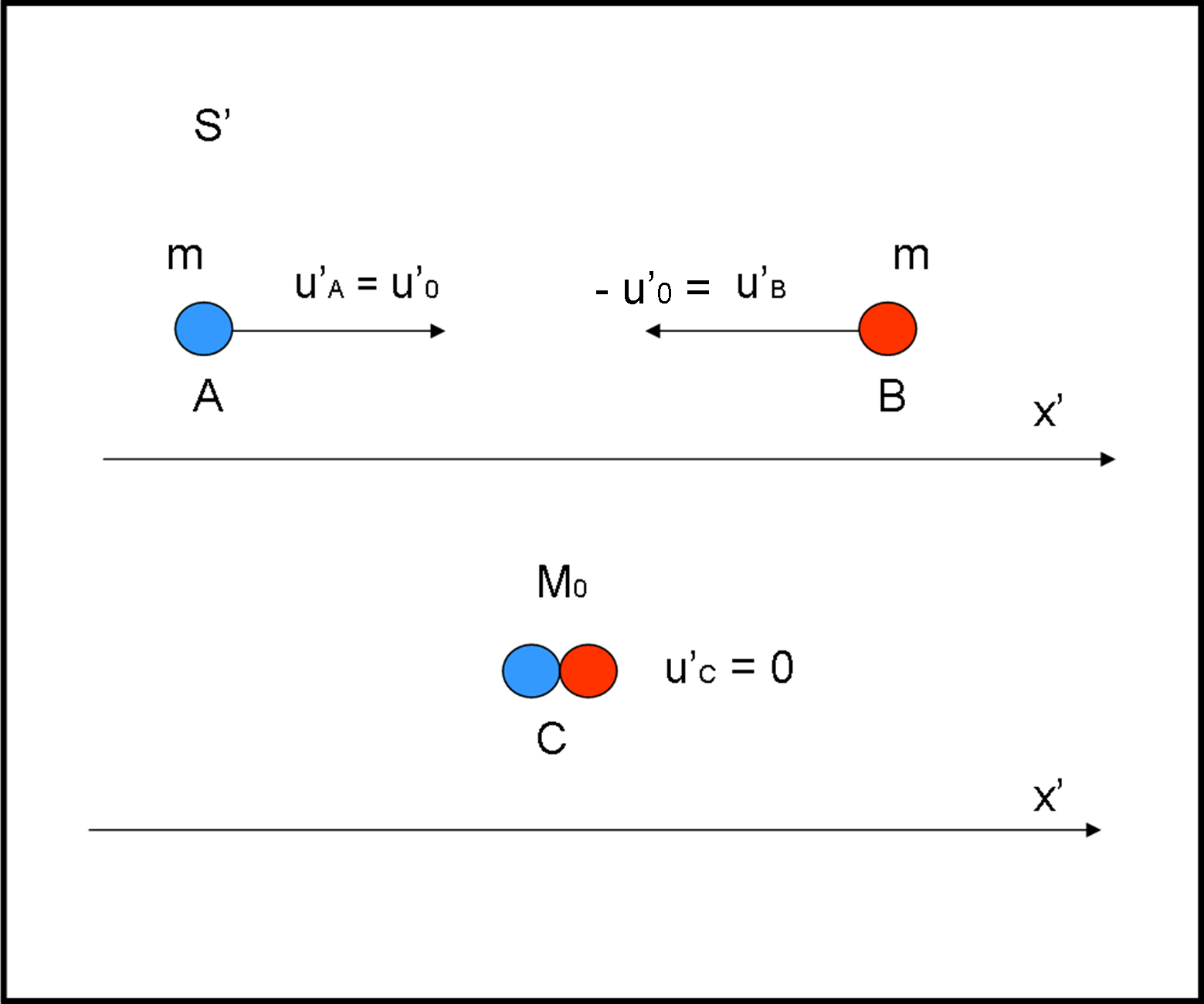
Vale, ovviamente:

u’_A = u’₀

e

u’_B = - u’₀

L’urto che avviene è completamente anelastico e dopo l’urto i due corpi viaggiano uniti (corpo C) con massa M e con una certa velocità u’_C. Per la conservazione della quantità di moto relativistica, devono coincidere le quantità di moto prima e dopo l’urto.

Prima dell’urto:

m₀ γ (u’_A) u’_A + m₀ γ (u’_B) u’_B = m₀ γ (u’₀) u’₀ - m₀ γ (u’₀) u’₀ = 0

Dopo l’urto:

M u’_C = 0

Da cui si ricava che u’_C = 0.

Il corpo C, unione dei due corpi A e B, rimane fermo e la sua massa è quella a riposo M₀.

Nella fisica classica sappiamo che M₀ = 2m₀ e che l’energia cinetica NON si conserva, dato che prima dell’urto vale 2 ½ mu'₀² e dopo l’urto vale 0. Abbiamo la conservazione della massa, ma non dell’energia cinetica.

Vediamo cosa succede in campo relativistico. Già ci dobbiamo aspettare che M₀ > 2m₀, ma c’interessa sapere cosa fa l’energia cinetica. Per cui rifacciamo il calcolo in un caso più generale.

Non ci resta che cambiare sistema di riferimento. La conservazione della quantità di moto deve, comunque, restare valida e a noi non resta che sfruttarla.

Consideriamo un sistema S in cui il corpo B risulti fermo (Fig. 2).

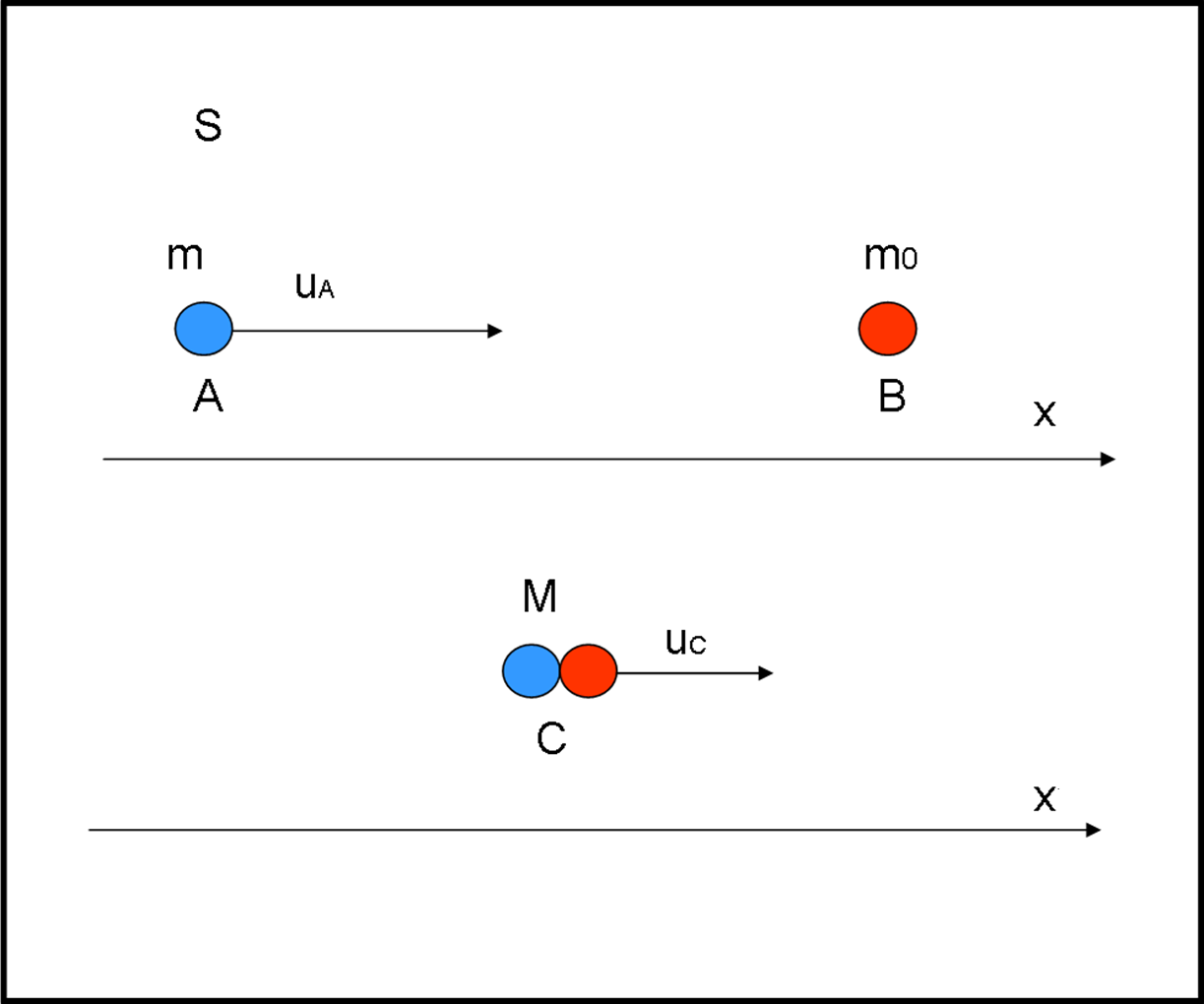
Ossia

u_B = 0

Esso vedrà S’muoversi con una velocità di trascinamento v = u’₀ (S si muove con velocità – u’₀  rispetto a S’).

Calcoliamo, ora, le velocità u_A e u_C, attraverso la ben nota formula di composizione relativistica delle velocità:

u = (u’ + v)/(1 + u’v/c²)           (formula generale, tanto per richiamarla…)

Nel nostro caso:

u_A = (u’_A + v)/(1 + u’_A v/c²) = (u’₀ + u’₀)/(1 + u’₀ u’₀/c²) = 2u’₀/(1 + u’₀²/c²)   …. (11)

u_C = (u’_C + v)/(1 + u’_C v/c²) = 0 + u’₀/(1 + 0·u’₀/c²) = u’₀        …. (12)

Per la conservazione della quantità di moto nel sistema S deve allora essere:

m₀ γ(u_A) u_A + m₀ γ(u_B) u_B = M₀ γ(u_c) u_C

e quindi:

m₀ γ(u_A) u_A + 0 = M₀ γ(u^’₀) u’₀

m₀ u_A/(1 – u_A²/c²)^1/2 = M₀ u’₀/(1 – u^’₀²/c²)^1/2

Non ci resta che sostituire la u_A trovata con la (11)…

Sono passaggi algebrici semplici e un po’ noiosi, ma fanno molto bene come esercizio. Li lascio a voi! Il risultato comunque è:

2 m₀ u^’₀/(1 – u’₀²/c²) = M₀ u’₀/(1 – u^’₀²/c²)^1/2

Da cui:

2 m₀ /(1 – u’₀²/c²)^1/2 = M₀          ….(13)

E, quindi:

M₀ > 2m₀

Come già trovato nell’articolo passato: le masse a riposo non si conservano.

Dalla uguaglianza tra massa ed energia, la relazione  (13) ci dice, però,  che anche l’energia a riposo del corpo C di massa M₀ è maggiore delle energie a riposo della somma delle masse a riposo di A e B. Infatti basta moltiplicare a sinistra e a destra per c² per avere le energie a riposo.

M₀c² > 2m₀c²

Tuttavia, la stessa relazione (13) ci dice anche che l’energia totale del sistema si è conservata nell’urto.

Consideriamo nuovamente il sistema S’, dove le due masse A e B andavano una contro l’altra e formavano una massa C immobile.

In questo sistema l’energia totale prima dell’urto (E_P) è data dalla somma delle due energie totali di ogni particella. 

E_PA = E_PB = mc² = m₀γ(u’₀) c²

E_P = E_PA + E_PB = 2m₀γ(u’₀)c² = 2m₀ c²/(1 – u’₀²/c²)^1/2

Dopo l’urto, l’energia totale E_D non è altro che quella a riposo di C

E_D = M₀c²

Ma, sostituendo al posto di M₀ la relazione (13), si ottiene.

E_D = 2 m₀ c²/(1 – u’₀²/c²)^1/2

E, quindi:

E_P = E_D

Anche negli urti anelastici l’energia totale si conserva!

In conclusione, partendo dalla legge di conservazione della quantità di moto relativistica, si ottiene che l’energia totale del sistema si conserva in qualsiasi sistema di riferimento inerziale. Al contrario di quanto avveniva in meccanica classica, in qualunque tipo di urto si deve conservare sia la quantità di moto relativistica che l'energia relativistica.

Riassumendo: la conservazione dell'energia rappresenta una legge valida per qualunque fenomeno fisico e vale in qualunque riferimento inerziale, in accordo con il principio di relatività.

Il “succo” fisico di questo esperimento è ormai facilmente comprensibile: le masse a riposo non si conservano così come le energie cinetiche, ma si conserva l’energia totale. Una dimostrazione lampante e decisiva che massa ed energia sono la stessa cosa!

Che dire? Un risultato sconvolgente nella sua semplicità e nella sua importanza rivoluzionaria. Non possiamo che considerare la teoria della relatività ristretta un vero capolavoro assoluto (qualcosa di … assoluto c’è!). Non ci resta che ammirarlo, come la Gioconda, ma sapendo finalmente cosa vuole rappresentare (non è una foto ben riuscita di un viso sorridente, ma la Natura che prende coscienza di se stessa).

Ancora un passo (forse ancora più fondamentale) e poi possiamo riposarci un po’…