Categorie: Matematica Teoria degli insiemi
Tags: cantor insiemi
Scritto da: Umberto Cibien
Commenti:13
Gli infiniti di Cantor. Parte prima: gli Insiemi
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Già nell'antica Grecia era noto il concetto di infinito, Galileo aveva già compreso a quali paradossi può portare, ma la formulazione matematica rigorosa è dei tempi moderni (circa nel 1878) ed è dovuta a Georg Cantor. Il grande matematico David Hilbert disse di lui:
« Nessuno riuscirà a cacciarci dal Paradiso che Cantor ha creato per noi. »
Per arrivare nel Paradiso di Cantor, dobbiamo prima introdurre due concetti fondamentali della matematica moderna; gli insiemi e le corrispondenze. In questo articolo ci occuperemo degli insiemi. Non voglio farlo in modo formale, ma intuitivo.
Tutti sappiamo intuitivamente cosa intendiamo dire per "insieme"; possiamo parlare di una collezione di oggetti di vario tipo, che possono essere lettere, numeri, parole, ecc. Basta dare una regola per determinare gli elementi di un insieme. Ad esempio se definisco come A l'insieme delle capitali Europee, sono in grado di rappresentare A per elencazione, ovvero: A={Roma,Parigi, Berlino,Atene,...}
Gli oggetti di un insieme si dicono elementi dell'insieme. La notazione formale per indicare l'appartenenza di un elemento a all'insieme A è . L'insieme vuoto (che si indica con
) è un particolare insieme che si introduce così: " l'insieme che non ha nessun elemento".
Sottoinsiemi.
Un insieme A è sottoinsieme di un altro insieme B quando tutti gli elementi di A appartengono anche a B. Possiamo rappresentare gli insiemi con i diagrammi detti di Eulero-Venn. Nelle figura sotto vediamo come A sia sottoinsieme di B.
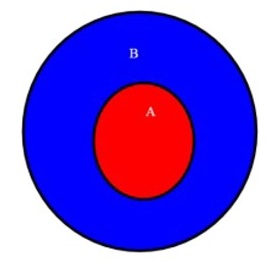
Se A è l'insieme delle capitali Europee, chiaramente A è un sottoinsieme delle città Europee B. Affermiamo poi che l'insieme vuoto è sottoinsieme di qualsiasi insieme (e lo giustifichiamo più avanti quando parleremo di unione fra insiemi). Bisogna però distinguere due casi di sottoinsiemi di un insieme B: i sottoinsiemi propri e quelli impropri. A è un sottoinsieme proprio se ci sono elementi di B che non appartengono ad A (come nell'esempio). Mentre invece A è sottoinsieme di se stesso (qualsiasi sia A), ma in tal caso è un sottoinsieme improprio.
L'inclusione propria di A in B si indica con
L'inclusione impropria di A in B si indica con
Operazioni fra insiemi.
Intersezione fra insiemi. L'insieme intersezione di A con B (che si indica con ) è un terzo insieme C costituito dagli elementi che sono sia in A che In B.(esempio: se A={a,b,c,d} e B={a,b,e,f} l'intersezione
è l'insieme C={a,b}. Se non hanno elementi in comune, gli insiemi si dicono disgiunti. In tal caso l'intersezione è l'insieme vuoto.

Unione di due insiemi. L'insieme unione di A con B (che si indica con A U B) è l'insieme formato da tutti gli elementi di A e B presi una sola volta; se A e B sono quelli dell'esempio sopra, A U B={a,b,c,d,e,f}.
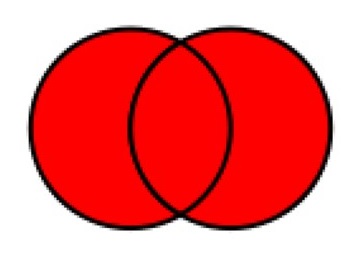
Notiamo che qualsiasi sia A; in particolare se
(insieme vuoto) allora
. Quindi abbiamo dimostrato l'affermazione sopra, cioè che l'insieme vuoto è sottoinsieme di qualsiasi insieme.
L'insieme prodotto
Un particolare insieme che ci servirà è l'insieme prodotto. Definiamo insieme prodotto di A con B (e lo indichiamo con A x B) l'insieme delle coppie che si ottengono prendendo un elemento da A e uno da B in tutti i modi possibili. Se A e B sono A={a,b} e B={e,f}, l'insieme prodotto è costituito dai seguenti elementi:
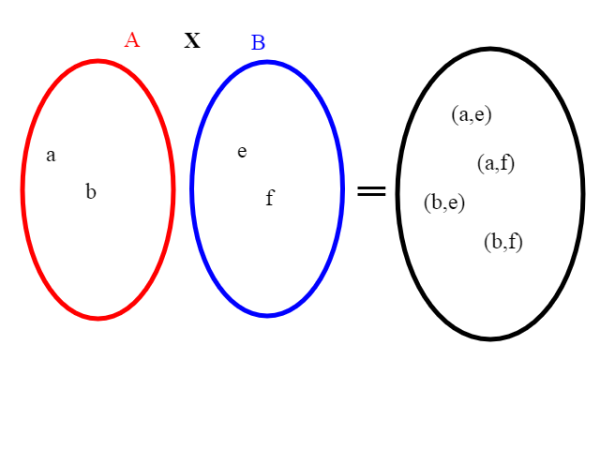
A X B = {(a,e),(a,f),(b,e),(b,f)}. Notiamo che se A ha n elementi e B m elementi l'insieme prodotto ha n *m elementi.
Cardinalità di un insieme
Fino ad ora abbiamo considerato esempi di insiemi finiti (ossia di insiemi di cui è possibile contare il numero di elementi. La cardinalità di un insieme A (che si indica con |A| è semplicemente il numero dei suoi elementi.
Insiemi numerici
Particolari insiemi che i serviranno sono gli insiemi numerici, che tutti conosciamo. A parte la descrizione, vogliamo brevemente ricordare come gli insiemi numerici si siano evoluti per soddisfare delle esigenze di calcolo e di risoluzione di problemi.
L'insieme N dei numeri naturali (quelli che servono per contare, e tutti conosciamo fin da bambini)
N={0,1,2,3,4,.....}
Nell'evoluzione della matematica, ci si accorse che i numeri non servono solo per contare, ma anche per le operazioni di somma, sottrazione e divisione.
L'insieme Z dei numeri relativi:
Z={...,-5,-4.-3,-2,-1,0,1,2,3,4,5,...}
sono un estensione dei numeri naturali, che nasce dalla necessità di ampliare le sottrazioni a-b con b maggiore di a (che non dà risultato positivo), oltre che ad esprime quantità fisiche come la temperatura o l'altitudine al di sotto di uno zero fissato.
L'insieme Q dei numeri razionali, è l'insieme di tutte le frazioni p/q, con p, q numeri relativi e .
I numeri razionali sono una estensione dei numeri relativi e servono per risolvere le equazioni del tipo 3x=2, in quanto 2/3 non è un intero, quindi la soluzione non esiste nell'insieme dei relativi.
L'insieme R dei numeri Reali
Nemmeno i numeri razionali bastano per risolvere certi problemi; non è un numero razionale (che per il teorema di Pitagora non è altro che l'ipotenusa di un triangolo rettangolo di cateti 1,1).
Infatti per il teorema di Pitagora: per risolvere dobbiamo trovare il numero che elevato al quadrato dà 2; ma questa è proprio la definizione di
.

Radice di 2 non è un numero razionale; Infatti se fosse un numero razionale, potremmo prendere la frazione che lo rappresenta (p/q) con p e q primi fra loro. Ma se
allora elevando al quadrato
....1)
ma allora è un numero pari; ma allora anche p è pari (perchè il quadrato di un numero dispari è dispari, basta fare il quadrato del binomio 2n+1 per rendersene conto), quindi posso scrivere p=2k; sostituendo nella 1) ottengo:
dividendo ambo i membri per 2:
; quindi anche q è pari ma questo contraddice l'affermazione che p e q siano primi fra loro.
Da qui la necessità di introdurre un nuovo insieme numerico, quello dei numeri reali, che contiene anche i numeri detti "irrazionali".
Esistono le seguenti inclusioni: (come è logico, essendo ciascun insieme una estensione dell'altro).
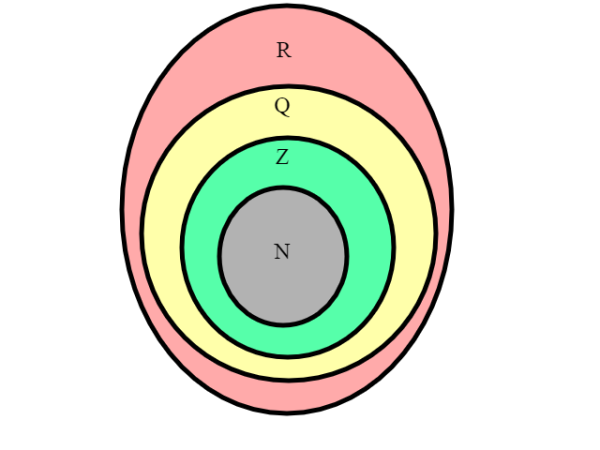
A differenza degli esempi precedenti, questi insiemi non sono finiti, ovvero non riusciamo a contare il numero degli elementi, quindi a definirne la cardinalità. Vedremo come superare questo ostacolo.
Quello che è stato trattato sugli insiemi è sufficiente per proseguire nel viaggio verso il Paradiso di Cantor.
Nel prossimo articolo ci occuperemo delle corrispondenze fra insiemi.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica






13 commenti
La matematica degli insiemi è qualcosa di meraviglioso. Ha bisogno solo di un minimo di capacità di astrazione... Io mi ricordo l'esame di geometria 3, fatto con il fratello di Paolo Conte, preside della facoltà di matematica. Insieme si riuscivano perfino a disegnare filtri, ideali, spazi connessi e compatti e mille altri concetti che, se visti nel modo giusto, sono più affascinanti delle cose veramente concrete. E a ben vedere descrivono perfettamente la realtà che ci circonda...
Non abbiate paura a chiedere chiarimenti a Umberto. Come sempre, molte cose che sembrano ovvie non lo sono. Basta solo seguirle con attenzione e non vergognarsi di non aver capito. Probabilmente, sarà il primo a chiedere aiuto...
Forza, si sta aprendo un nuovo mondo, un nuovo metodo di pensare...
Bene così, avanti con Cantor
Scusa Umberto, abbi pazienza, ma per me è un argomento nuovo.
Ho bisogno di capire meglio alcuni passaggi.
Non mi è chiara la definizione di sottoinsieme improprio.
Ammettiamo che B sia composto da 50 elementi di tipo a; b, c e d, e che A sia composto da 30 elementi di tipo a, b, c e d, si tratta di un sottoinsieme improprio?
Prima di proseguire devo capire meglio questo passaggio..
Paolo
Quando dico che A è composto da a; b, c e d questi sono tutti gli elementi di A; non ce ne sono altri. Ho elencato tutti gli elementi dell'insieme. Non esiste un "tipo". In pratica volevo dire che l'unico caso di sottoinsieme improprio è solo L'insieme A stesso. Se invece prendiamo sottoinsiemi di A tipo C={a,b} che sono strettamente inclusi in A (ovvero, dalla definizione esistono elementi di A che non ci sono in C), allora questi sono sottoinsiemi propri.
Forse non sono stato abbastanza chiaro; l'unico sottoinsieme improprio di un insieme A è sempre e comunque tutto l'insieme A.
Grazie Umberto, ora ho capito.
Paolo
grazie a te per l'interesse dimostrato
ed io invece non ho capito
perché e impropria l'inclusione di A in AUB dato che ci sono elementi di AUB che non appartengono ad A perché apparterrebbero solo a B
Gianni, hai fatto bene a sottolineare questo fatto, asserisco che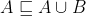 ; questa è una condizione meno forte della condizione
; questa è una condizione meno forte della condizione  , ed è valida sempre,mentre
, ed è valida sempre,mentre  non è valida nel caso A=B. (potrebbe anche essere A=vuoto=B,non c'è inclusione stretta. Scrivendo
non è valida nel caso A=B. (potrebbe anche essere A=vuoto=B,non c'è inclusione stretta. Scrivendo 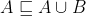 ho solo applicato la definizione di inclusione impropria, ogni elemento di A sta in A U B. In pratica se non so niente di come siano fatti A e B, mal'inclusione impropria va sempre bene . In pratica la scrittura
ho solo applicato la definizione di inclusione impropria, ogni elemento di A sta in A U B. In pratica se non so niente di come siano fatti A e B, mal'inclusione impropria va sempre bene . In pratica la scrittura 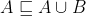 non basta per dire che A è sottoinsieme improprio di A U B ed è diverso da A; infatti in tal caso A=B= A U B.Comunque concordo con te che le definizioni possono portare a confusione. Purtroppo tutti usano queste.
non basta per dire che A è sottoinsieme improprio di A U B ed è diverso da A; infatti in tal caso A=B= A U B.Comunque concordo con te che le definizioni possono portare a confusione. Purtroppo tutti usano queste.
ci ho messo un po' ma ho capito
l'inclusione impropria siamo sicuri che vale sempre, quella propria costringerebbe a precisazioni che non è detto che aiutino a formulare bene ulteriori ragionamenti logici
Gianni, mi ha fatto piacere che tu abbia approfondito
Si, se sappiamo che A è contenuto in B, ovvero che ogni elemento di A appartiene anche a B, si usa il simbolo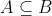 quando non si è certi se
quando non si è certi se 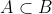 oppure A=B .
oppure A=B .
La bellezza della matematica... se hai voglia di farti trasportare da lei, è un'astronave fantastica!