Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Una grandezza che non varia cambiando sistema è veramente ovvia: l’energia a riposo di una certa massa (a riposo) m₀. Essa è il prodotto tra la massa a riposo (che è quella che è ovunque) e il quadrato di una costante che più costante non si può: la velocità della luce c.

Sì, va bene… ma è poca cosa, in realtà. Sarebbe molto meglio trovare qualcosa di più articolato che contenga sia l’energia totale (e quindi la massa relativistica) sia la mia tanto amata quantità di moto (giuro che non sono stato io a suggerirlo a Einstein, ha fatto tutto da solo…).

Una cosa complicata? Nemmeno per sogno, l’abbiamo già tra le mani, basta scriverla nel modo giusto.

Tanto per cambiare, partiamo dalla massa relativistica:

m = m₀/(1 - v²/c²)^1/2

Tuttavia, volendo far comparire le energie è molto meglio elevare a quadrato:

m² = m₀²/(1 - v²/c²) = m₀² c²/(c² - v²)

e, ancora:

m²(c² - v²) = m₀²c²

Per far comparire le energie dobbiamo ancora moltiplicare entrambi i membri per c² e si ottiene:

m²c⁴ - m²v²c² = m₀²c⁴

m²c⁴ = m₀²c⁴ + m²v²c²

Attenzione, però:

m₀c² è l’energia a riposo E₀

mv e la quantità di moto relativistica q

mc² è l’energia totale E

La relazione di prima ci dice che l’energia totale E risulta uguale a:

E² = E₀² + q²c²

Essa crea un legame indissolubile tra energia totale, energia a riposo e quantità di moto. La sua importanza è di carattere sia pratico (è meglio lavorare in termini di energia e quantità di moto che non direttamente con le masse) che teorico (accenneremo soltanto a una fantastica conseguenza…).

Ancora più rivoluzionaria è la stessa espressione scritta così:

E₀² = E² - q²c²    …. (1)

Perché è cosi importante? Presto detto: il primo membro è una quantità che risulta invariante per qualsiasi sistema di riferimento inerziale (è l'energia a riposo). Deve perciò esserlo anche il secondo membro, ossia:

E² – q²c² = costante

Abbiamo trovato un’altra grandezza che è un invariante relativistico, al pari dell’ormai celebre distanza relativistica s² (ricordate Minkowski, dopo la Fig. 19 ?). Dimostreremo anche, malgrado sembri quasi impossibile, la perfetta similitudine tra s² e E² – q²c² .

Cominciamo a notare (ma ci torneremo sopra) che:

 s² = t²c² – d²        …. (2)

dove d è la distanza spaziale classica:

d² = x² + y² + z²

Notiamo ancora che x, y, z possono essere considerate le componenti del vettore spazio d, mentre t è uno scalare.  Parlando di Minkowski avevamo considerato solo la componente x e avevamo posto T = ct, ma la formula è sempre la stessa. In quel caso avevamo scritto:

s² = T² – x²

che è esattamente la (2).

Nel nuovo invariante, abbiamo di nuovo un vettore (quantità di moto q, con le sue tre componenti) e uno scalare (energia E).

Ma...ci torneremo sopra tra non molto. Ogni cosa a suo tempo.

Torniamo, momentaneamente, alla (1) e notiamo come possa essere interessante descrivere attraverso un grafico la relazione tra q ed energia E. La funzione da studiare è:

q = (E² – E₀²)^1/2/c

Potete provarci tranquillamente voi, prima di proseguire. Il tutto si riduce, in fondo, a trovare un asintoto obliquo (un bell’esercizio per non dimenticare la … matematica)

Ovviamente, per q = 0, abbiamo E = E₀

Mentre l’asintoto ha equazione

q = E/c

Il grafico è quello rappresentato in Fig. 1.

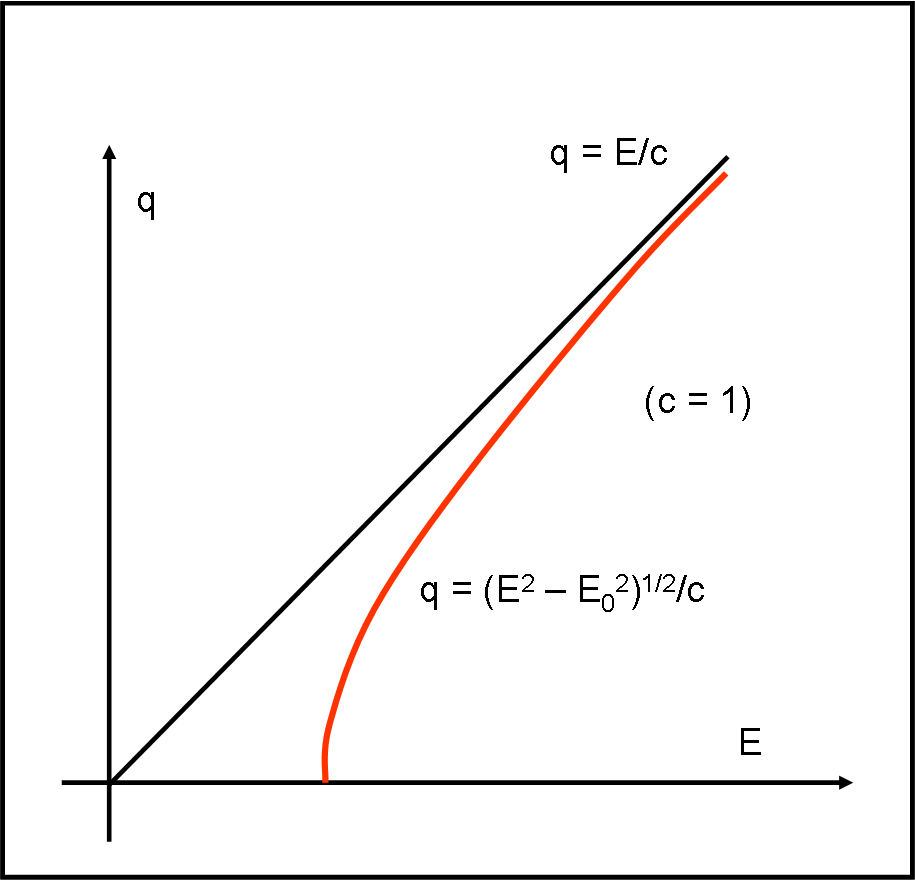
in campo ultrarelativistico abbiamo che E₀ è del tutto trascurabile e si ha:

E ~ qc

L'energia è, in pratica, nient'altro che la quantità di moto (con le dovute unità di misura).