Innanzitutto, i miei più vivi complimenti a coloro che hanno affrontato e risolto il paradosso. Mi hanno dato una grande soddisfazione! Sono anche convinto che molti altri hanno fatto lo stesso, anche se non hanno voluto uscire allo scoperto.

In realtà, hanno ragione entrambi i papalli e le figure sono entrambe giuste nel loro sistema di riferimento. Quello rosso considera se stesso fermo e quindi è sicuro che la luce parta dal punto che occupa. Ma la stessa cosa viene pensata dal papallo blu. La costanza della velocità della luce deve dare ragione a entrambi. Il paradosso si scioglie, accettando la non simultaneità in sistemi inerziali con velocità relativa non nulla.

In altre parole, entrambi rimangono al centro del cono di luce che parte dall’origine. Ciò che cambia è solo e soltanto il sistema di riferimento se visto da uno o dall’altro. Il tutto è perfettamente simmetrico. Il diagramma di Minkowski spiega come questo possa essere rappresentato con una sola figura.

La Fig. 1 illustra ciò che vede il sistema rosso al suo tempo rosso t = 1, come mostrato la volta scorsa.

Analogamente fa la Fig. 2 per il sistema blu al suo tempo blu t = 1

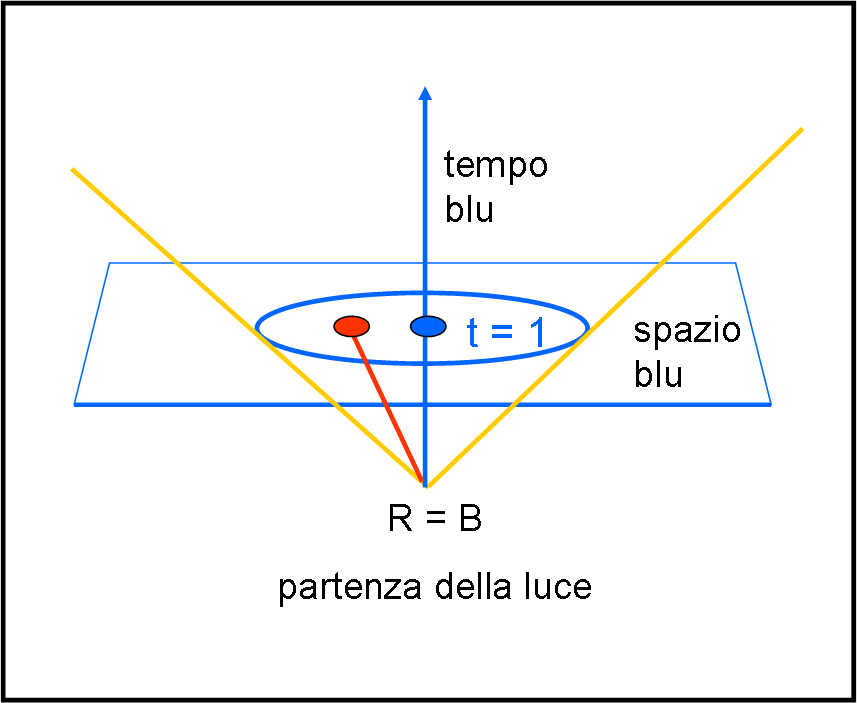
I tempi rosso e blu sono IDENTICI se misurati all’interno del proprio sistema, ma sono DIVERSI se osservati dall’altro sistema. Il diagramma di Minkowski riesce a spiegare perché le Fig. 1 e 2 sono entrambe vere se i tempi sono quelli misurati dagli orologi del proprio sistema, con tempi e spazi che seguono le trasformazioni di Lorentz.

La Fig. 3 mostra la situazione con il sistema rosso immaginato fermo. Il sistema blu si muove con velocità v e quindi il suo tempo scorre lungo l’asse blu. Il suo spazio ruota di conseguenza. Allo scoccare del tempo unitario rosso, il sistema rosso “vede” il papallo blu nel suo tempo rosso, in una posizione laterale che corrisponde a un tempo, per il papallo blu, che è ancora inferiore alla sua unità (cerchio blu aperto). L’unità di tempo blu viene raggiunta dal papallo blu quando la posizione di questo (cerchio blu pieno), vista dal sistema rosso, corrisponde a un tempo decisamente maggiore dell’unità di tempo rossa (dilatazione dei tempi). Per il papallo rosso l’orologio di quello blu gira più lentamente. Tuttavia, lo stesso capita per il papallo blu, quando raggiunge il suo tempo unitario. In quel momento, la simultaneità gli fa vedere il papallo rosso a un tempo inferiore all’unità di tempo rosso. O, se preferite, il papallo rosso raggiunge la sua unità di tempo a un tempo blu che è maggiore dell’unità di tempo del papallo blu. Per il papallo blu è il tempo di quello rosso che va più lentamente.

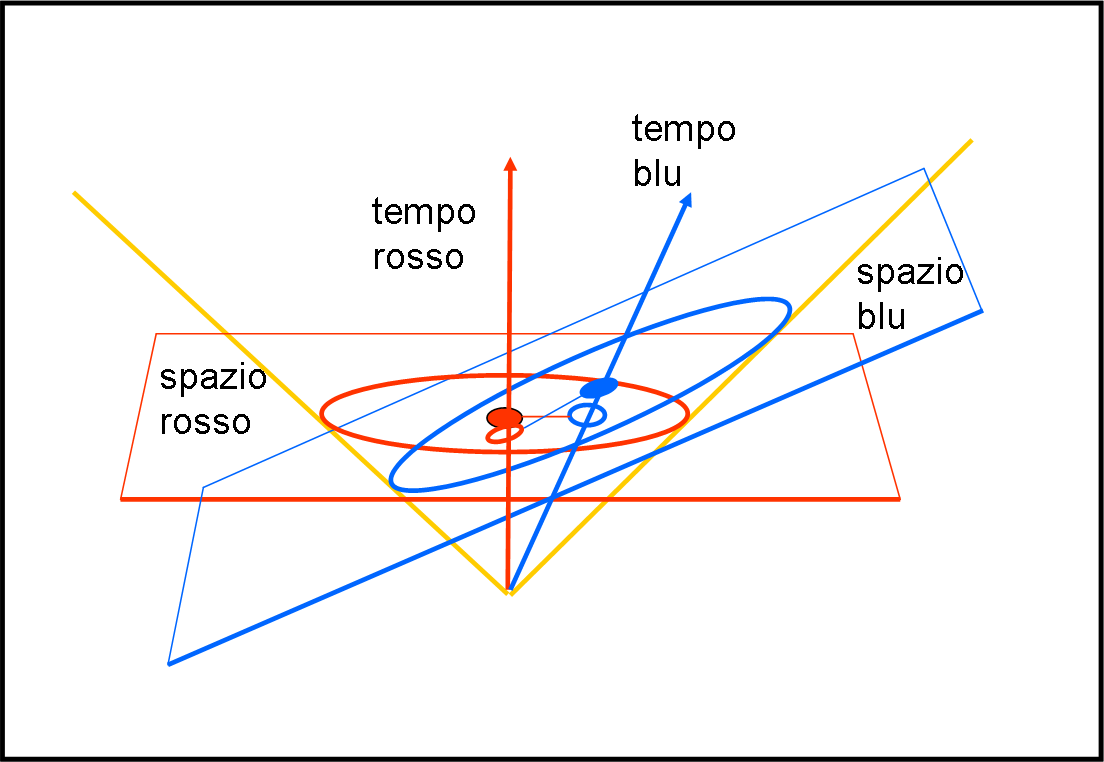
Se il sistema di riferimento, considerato fermo, diventa quello del papallo blu, tutto si ribalta (Fig. 4), mantenendo un’esatta simmetria. In questo caso è il sistema rosso che si muove con velocità – v.

La Fig 3 e la Fig 4 sono esattamente La Fig. 1 e la Fig. 2, quelle mostrate la volta scorsa, ai due tempi unitari. Il diagramma di Minkowski permette di disegnarle entrambe, qualsiasi sia il sistema di riferimento. Notate che il cono di luce rimane sempre lo stesso, dato che si riferisce al punto da cui è partita la luce, per entrambi i sistemi. Anche il suo "diametro", all'istante unitario, resta lo stesso (contrazione delle lunghezze... meno facile da vedere direttamente). Basterebbe, però, pensare che, cambiando sistema di riferimento, quello scelto come fermo mantiene sempre lo stesso diametro dell'onda di luce al suo tempo unitario.

Niente da fare, Minkowski è proprio un genio, capace di sintetizzare graficamente l'intera teoria di Einstein!

Il quiz è stato proposto QUI

Il prossimo quiz sarà un po’ più duro da risolvere, anche se graficamente molto più semplice.