Questo è soltanto un gioco (se volete… chiamatelo pure un quiz) che serve come porta d’ingresso per il nuovo teatro astronomico che andremo a scoprire tra poco.
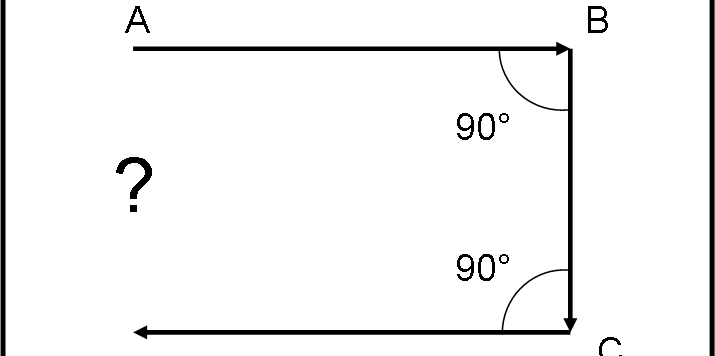

Questo è soltanto un gioco (se volete… chiamatelo pure un quiz) che serve come porta d’ingresso per il nuovo teatro astronomico che andremo a scoprire tra poco.

Bando alle ciance e andiamo dritti fino alla prima legge di Keplero, la parte più difficile, che ci obbliga a prendere per buona la soluzione di un’equazione differenziale. Per noi è, al momento, troppo impegnativa, ma chi vuole saperne di più trova un link adeguato.

Scusatemi ancora, ma in questo circolo sento il bisogno di esprimere tutti miei sentimenti, emozioni e riflessioni. Non picchiatemi e, se vi sto stufando, saltate queste ripetitive esternazioni di una persona che cerca di comprendere prima di tutti se stesso. La Scienza vera non mancherà di certo...
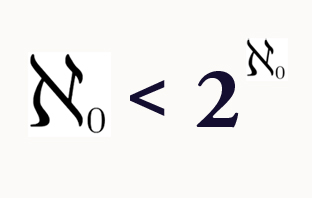
Nell'articolo precedente, abbiamo visto che anche Q è numerabile. Esistono insiemi non numerabili? Si, e lo dimostreremo in modo generale, arrivando ad un risultato di notevole importanza: non esiste un insieme di cardinalità maggiore di ogni altro insieme.
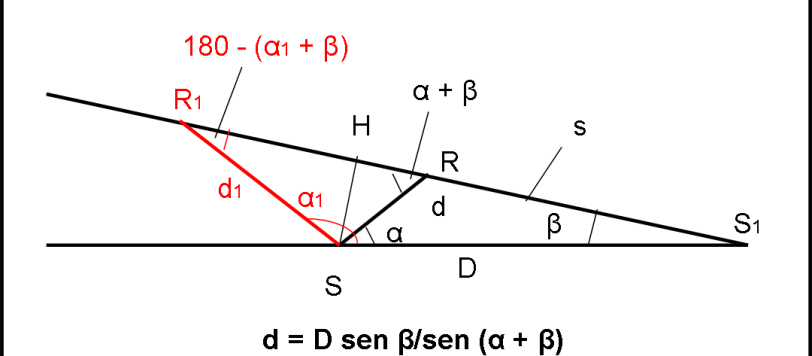
Ecco le soluzioni ai due quiz sulla costruzione del cielo visto da un’altra stella. La prima è ovvia, la seconda ha diverse possibilità. Io ho descritto quella che mi sembra più semplice, senza introdurre (ancora) teoremi trigonometrici non affrontati. Ma è solo questione di tempo… non illudetevi!

Come si può rimpiangere carta e matita, quando si ha a disposizione un bel computer in grado di dare forma alle più sfrenate fantasie? Si può, si può... eccome se si può! E Vin-Census ce lo dimostra...
Anche se a qualcuno sembrerò monotono, volevo chiarire ancora meglio lo scopo di un certo tipo di articoli che sono apparsi sul nostro Circolo e che proseguiranno sotto le sapienti mani e la tenera sensibilità di Barbariccio e Daniccia, guidate dall’esperienza di Scherzy e Astericcio.
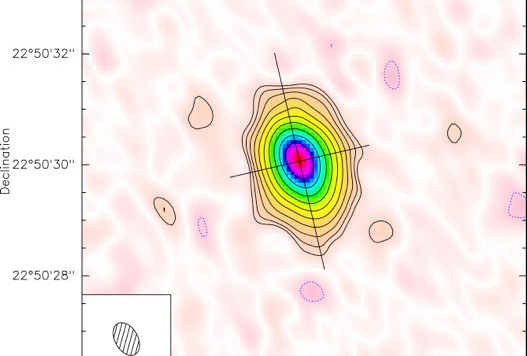
Abbiamo appena parlato di un pulcino planetario che potrebbe già essersi formato solo dopo un milione di anni dalla nascita della sua stella, ed ecco che un pianeta ben più grande di Giove conferma in pieno questo risultato abbastanza sconvolgente.

Ne abbiamo parlato da poco, ma sembra che i buchi neri galattici stiano conquistando sempre più un posto di rilevo nella ricerca astronomica, a tal punto che riferire sui nuovi lavori può portare a grande confusione, sia perché si ripetono spesso le stesse cose, cambiando di poco i dati di partenza e/o le strategie descrittive (ma gridando quasi sempre alla scoperta), sia perché si vorrebbero fare nascere in qualche modo, senza limite alla fantasia.

E’ ormai diventata una delle immagini astronomiche più celebri degli ultimi anni (almeno per noi). Stiamo parlando del disco proto planetario attorno alla giovanissima stella HL Tau, ripreso con emozionanti dettagli da ALMA. Ne abbiamo parlato più volte, quasi seguendo in tempo reale la nascita e la crescita dei pianeti in formazione. In realtà, non se ne sono ancora visti, ma ci sono dettagli che potrebbero farli intuire.

Un gruppo italiano ha, forse, rilevato, attraverso Chandra, due possibili “semi” per futuri buchi neri galattici. Potrebbe essere la soluzione di un problema non ancora risolto: crescono in fretta o partono già ben pasciuti?
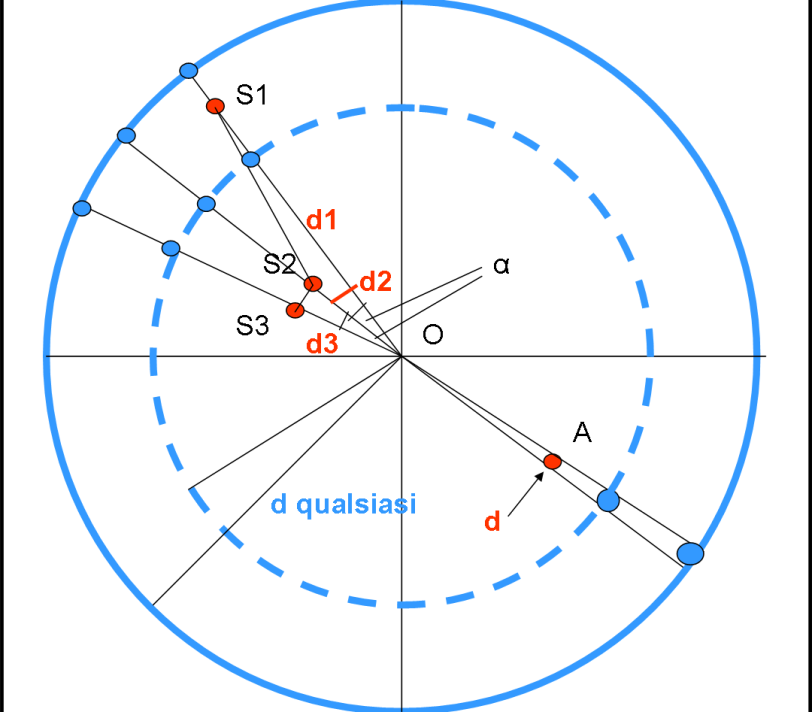
A volte si danno molte nozioni come acquisite. Poi ci si rende conto che quello che è ovvio per chi ha trafficato una vita con le posizioni di stelle e pianeti, proiettati sulla sfera celeste, potrebbe non essere così ovvio per molti altri. Tutti dobbiamo imparare qualcosa… e io per primo!

Chi ci ha dato le prove del Big Bang e dell’espansione dell’Universo? Forse, lo stesso Keplero, ma sicuramente Olbers nel 1826. Purtroppo, il suo paradosso non fu analizzato attentamente…
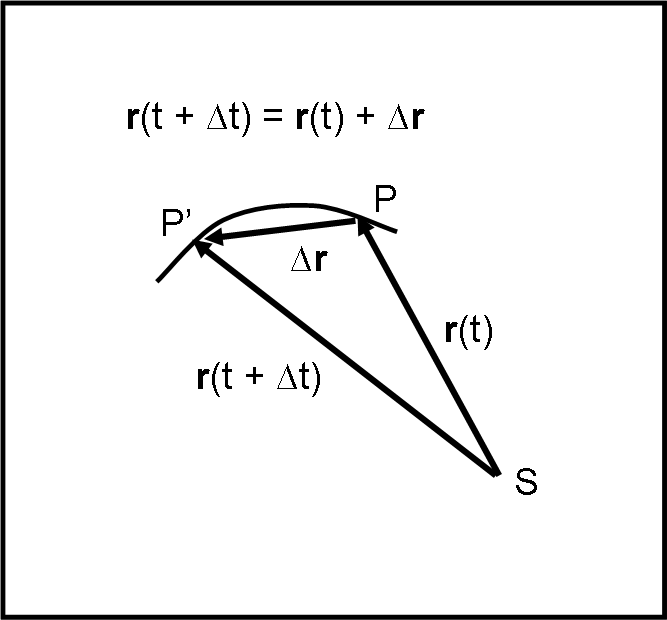
Quasi senza accorgercene abbiamo ricavato la seconda legge di Keplero. Soffermiamoci un poco su di lei e sul suo significato fisico. Poi proseguiremo verso la prima legge.

Parliamoci chiaro, cari amici: sono in pensione da circa otto anni, ho abbandonato per varie motivazioni (prima fra tutte la voglia di libertà) il “giro” accademico sempre più portato all’autocelebrazione, piuttosto che alla preparazione del futuro. E’ anche abbastanza comprensibile che durante quarant’anni di ricerca abbia sicuramente passato il periodo più fruttuoso per fare vera ricerca innovativa. Tuttavia…