La domanda era: “Potrei vedere, allo stesso istante t₀, l’oggetto in due posizioni diverse A₁ e A₂?” (QUI)

Rimanendo in campo realistico la risposta è NO e lo dimostriamo facilmente sia con una figura spaziale che con una spaziotemporale alla Minkowski. L’appetito, però, viene mangiando e, allora, abbiamo provato anche accettando situazioni fantascientifiche, ossia considerando la velocità della stella uguale o addirittura maggiore di quella della luce. Un esercizio non certo “scientifico” di per sé, ma interessante per comprendere sempre meglio i fenomeni dell’Universo.

Cominciamo con la soluzione geometrica più semplice, ma fisicamente plausibile, ossia imponiamo che la velocità di un qualsiasi corpo (grande o piccolo che sia) NON possa pareggiare o superare la velocità della luce. Costruiamo la Fig. 1 e spieghiamola per bene. Ne approfittiamo anche per ritornare su concetti ben noti, ma che non fanno mai male…

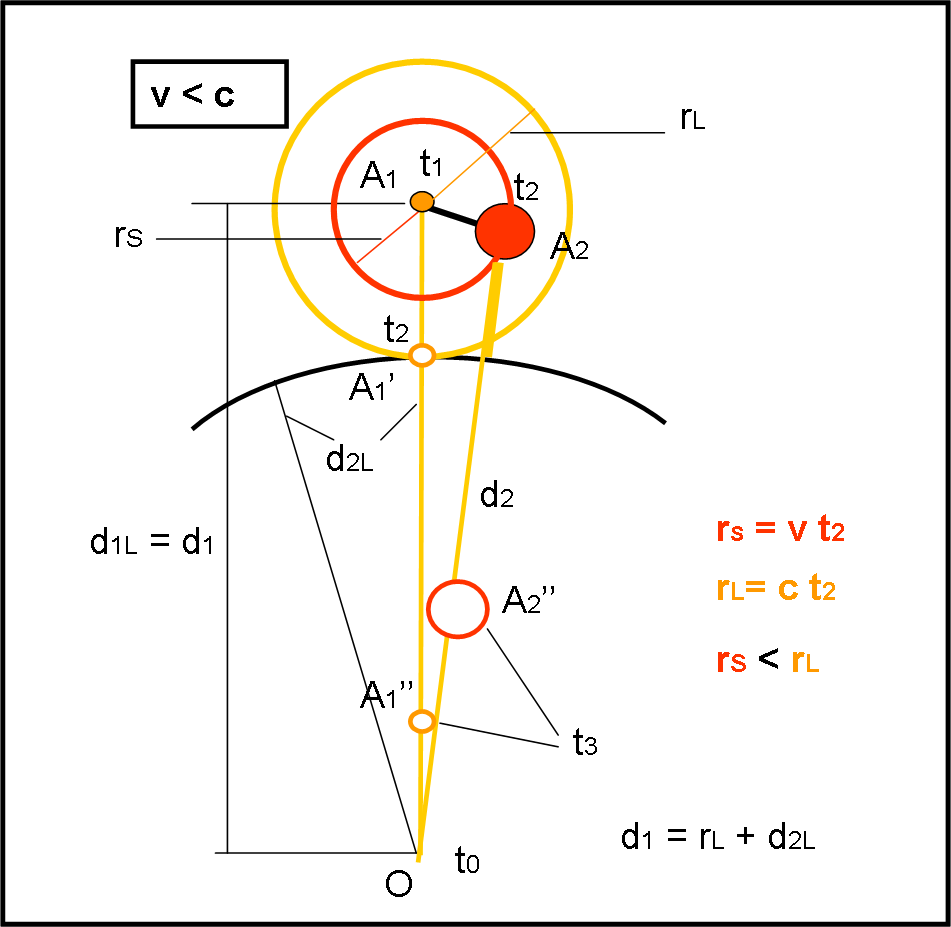
La stella A all’istante t₁ si trova in A₁. Per rendere più realistico il procedimento, immaginiamo che sia una stella come il Sole, in procinto di diventare una gigante rossa. In questo modo, abbiamo anche una visualizzazione immediata del tempo che passa per la stella.

Nella posizione A₁, la stella, ancora in sequenza principale, invia la sua luce. Al tempo t₂ (più vicino a t₀ = oggi), questa luce ha raggiunto il cerchio arancione di raggio r_L. A noi interessa solo il raggio luminoso diretto verso O (dove sta l’osservatore, ossia NOI).  In altre parole, l’immagine della stella partita da A₁, al tempo t₂, è il dischetto arancione aperto A₁’ che sta viaggiando verso di noi. Al tempo t₂ la distanza da percorrere è ancora d_2L. Partita la luce da A₁, la stella inizia a muoversi verso A₂. ne segue che questa è l’ultima luce inviata dalla stella nella posizione A₁.

Possiamo anche disegnare il cerchio di raggio d_2L e centro O, che indica il luogo dei punti nello spazio che potrebbero fare arrivare in O la loro luce, inviata al tempo t₂, nel medesimo istante t₀. Lungo questa circonferenza si trovano sia gli oggetti reali che inviano la loro luce in quel momento, sia le immagini di stelle molto più lontane che sono arrivate in quella posizione in quel momento: stelle un po’ “fantasma” che però si mostreranno tutte a noi allo stesso tempo t0. Un sistema ulteriore per capire che oggi stiamo vedendo oggetti vicini e lontani.

Disegniamo anche il cerchio rosso che è quello relativo alla velocità della stella A. Ossia, esso indica le posizioni A₂ che può aver raggiunto al tempo t₂ andando alla sua velocità v < c.

Ricapitolando, all’istante t₂ l’immagine di A₁ è nel punto di contatto tra la circonferenza arancione e quella nera (per costruzione), ossia in A₁’. L’immagine di A₂ è invece appena partita e può trovarsi solo lungo il cerchio rosso. Potete spostare A₂ dove volete lungo il cerchio rosso, ma la distanza d₂ = A₂O è sempre più lunga della distanza A₁’O = d_2L. Ne segue che l’immagine di A₂ arriverà sempre dopo quella di A₁.

Ad esempio, al tempo t₃ (molto più vicino a t₀ = oggi), vediamo la posizione relativa delle due immagini della stella A, quando era come il Sole e quando si è trasformata in gigante rossa.

Anche se la stella si muovesse esattamente verso di noi, l’immagine di A₂ resterebbe sempre dietro l’immagine di A₁, che è l’ultima partita dalla stella quando era in A1, di una distanza pari alla differenza dei raggi delle due circonferenze.

Con questo grafico abbiamo risposto alla domanda… Adesso comincia la parte fantascientifica.

L’ultimo caso particolare (stella che viaggia verso di noi), rende più interessante il primo caso fantascientifico, ossia quello con v = c.

La figura rimane la stessa, ma questa volta il cerchio rosso si sovrappone al cerchio arancione. Ne segue, quindi, che A₂, la gigante, può trovarsi ovunque lungo il cerchio arancione.

La faccenda non cambia rispetto a prima, dato che la distanza d₂ rimane “quasi” sempre maggiore di d_2L. Non proprio sempre, però! Nel caso che la stella si muova esattamente verso di noi, essa riuscirebbe a trovarsi al tempo t₂ proprio nella posizione di A₁’. In altre parole, l’immagine partita da A₁ e quella inviata da A₂ sono perfettamente sovrapposte. Se ne conclude che essere arrivano in O allo stesso tempo t₀. Le “vedremmo” sovrapposte, ma non in direzioni diverse.

Vi è, però, un grosso problema… Non solo le due immagini viaggiano di conserva, ma anche la stessa stella. Ciò vuole dire che nell’istante in cui le due immagini arrivano in O, ci arriva anche la stella! Se immaginassimo che la stella fosse ferma fino al tempo t₁ e si muovesse alla velocità della luce solo dopo quell’istante, cosa vedremmo nel cielo? Vedremmo sicuramente la stella Sole com’era un istante prima di t₀, ossia saremmo “colpiti” dall’immagine partita un istante prima di t₁. Sarebbe però l’ultima immagine visibile della stella e non solo… All’istante t₀ arriverebbe la stella vera e propria e quindi… non vedremmo più niente! Ultima luce e distruzione arriverebbero insieme

Ancora più assurdo sarebbe il caso in cui v > c (Fig. 2). Basta pensare che la figura invertirebbe il cerchio arancione con quello rosso. Nel caso della gigante rossa posta in A₂, la sua velocità maggiore della luce non basterebbe a farsi vedere prima di A₁. Continueremmo a vedere A₁ (prima) e A₂ (dopo) in tempi diversi. Qualitativamente non cambierebbe niente rispetto ai casi precedenti.

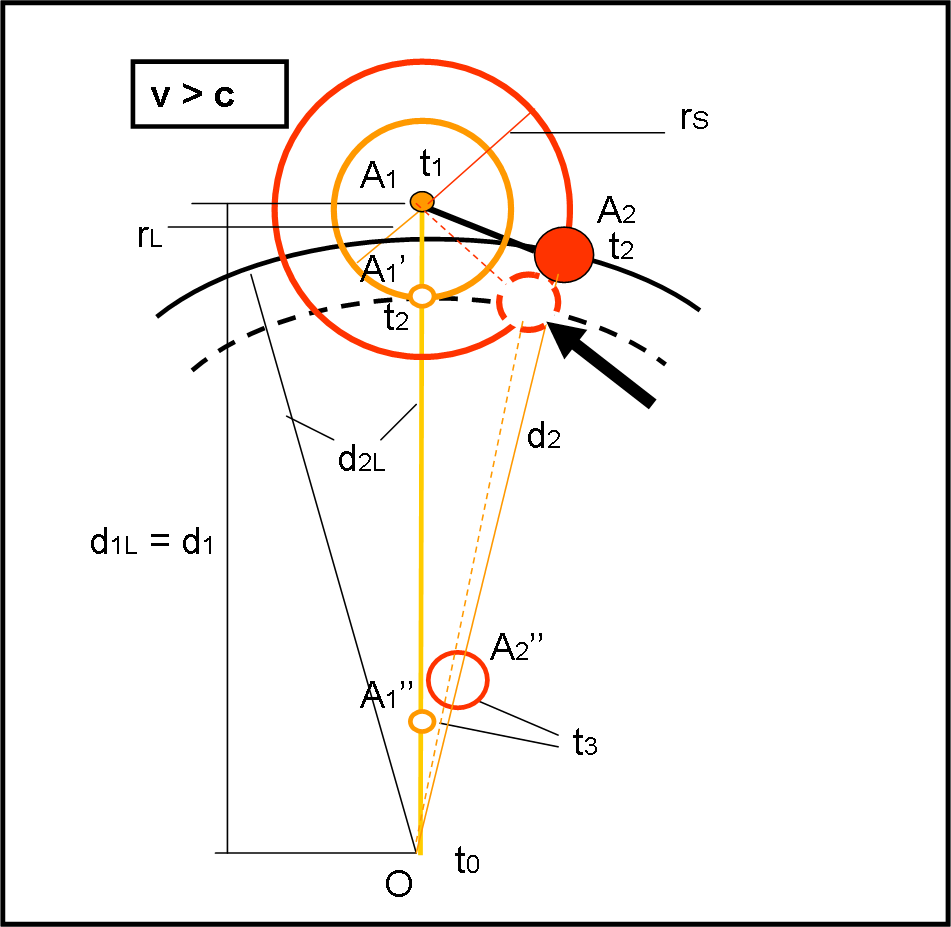
Il punto chiave corrisponde a quello relativo alla freccia nera (tratteggiato). La stella, viaggiando più veloce della luce, arriverebbe in A₂ in tempo perché la sua immagine, inviata al tempo t₂, debba ancora percorrere la stessa distanza da O dell’immagine mandata da A₁. Le due immagini giungono in O nello stesso tempo t₀, ma in direzioni diverse! In questo caso potremmo realmente vedere la stessa stella, nello stesso momento, in due direzioni diverse: in una è ancora come il Sole, nell’altra è già una gigante rossa.

Se la stella si dirigesse ancora di più nella nostra direzione ci sarebbe il ribaltamento: prima arriverebbe la luce di A₂ e dopo quella di A₁. Per comprendere meglio la situazione abbiamo inserito la Fig. 3, relativa a questo caso.

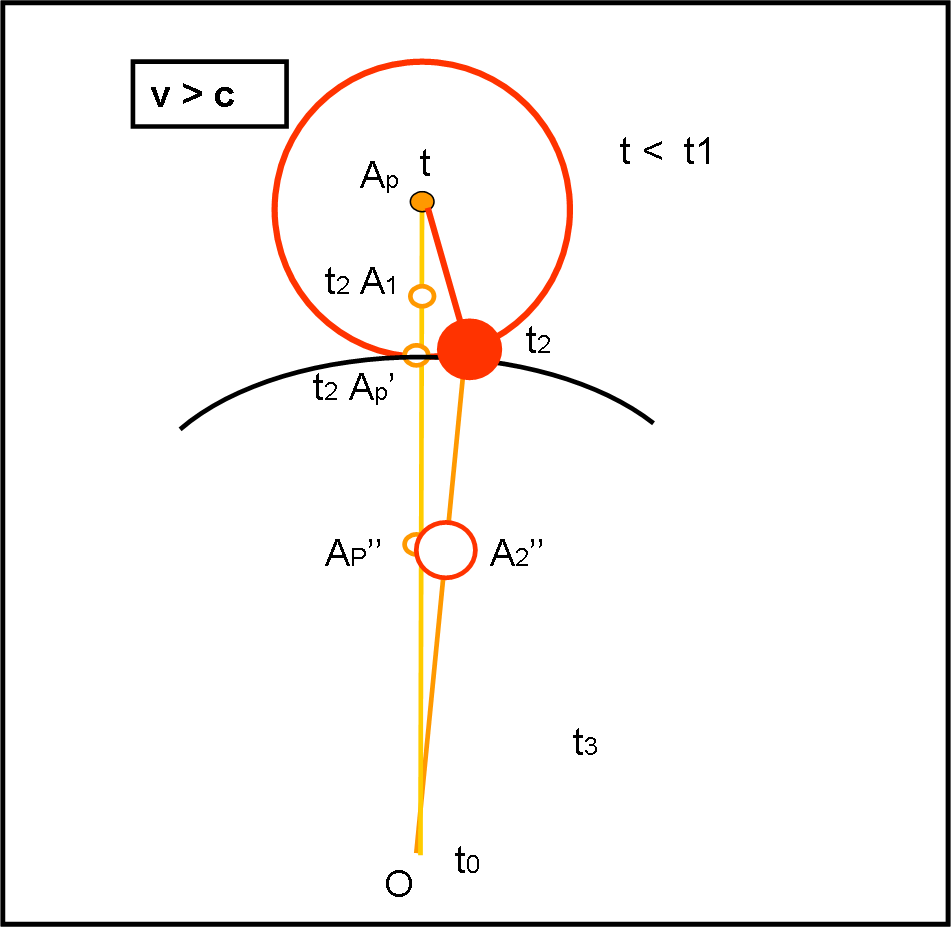
Vedremmo la gigante  A₂ prima di A₁ ancora in sequenza principale. Insomma un bel caos!! Ma la faccenda è ancora più complicata… Esisterebbe sempre un’immagine A_P, nata precedentemente ad A₁(t < t₁), che si trovi alla stessa distanza da noi dell’immagine inviata da A₂. In realtà, sarebbe la luce di A₂ che grazie alla stella iperveloce, “raggiungerebbe” la stessa distanza della luce partita da A_P. La stella permette alla sua immagine di raggiungere un’immagine partita precedentemente  a quella inviata al tempo t₁. Ci sarebbe, comunque, una visione contemporanea della stessa stella in due direzioni diverse, come nel caso precedente.

La faccenda diventa veramente complicata: passando alla fantascienza, anche un problemino semplice semplice può diventare tutt’altro che banale…

Si arriva comunque alla soluzione limite: la stella si muove proprio verso di noi. Teoricamente dovremmo vedere la stella gigante sempre in contemporanea con la stella tipo Sole, nella stessa direzione, tenendo conto che ci sarebbe sempre un’immagine della stella in sequenza principale che verrebbe raggiunta da quella inviata dopo. Il problema però si risolve velocemente. Dato che al momento t₁ la stella inizierebbe ad andare più veloce della luce, essa ci raggiungerebbe direttamente portando alla catastrofe, ben prima che la luce inviata da A₁ e da A₂ ci possa raggiungere. Saremmo raggiunti, infatti, da una gigante rossa (se a quella velocità ha avuto il tempo di evolvere). Ciò succederebbe ben prima che la luce inviata al tempo t₁ (e anche al tempo t₂) sia arrivata a noi, dato che la stella l’avrebbe raggiunta e superata. L’ultima cosa che vedremmo nel cielo è una stella come il Sole, mandata a un tempo molto precedente a t₁. Poi la catastrofe senza alcun preavviso.

L’intera faccenda si semplifica un po’ utilizzando il diagramma di Minkowski. Attenzione, però. Per potere realmente vedere una situazione come quella illustrata finora, dovremmo usare una rappresentazione con uno spazio di Minkowski bidimensionale. Sarebbe troppo per noi. Limitiamoci, allora, al caso in cui la direzione A₁O sia proprio quella del movimento della stella. in questo caso possiamo ridurre tutto al solito piano spaziotemporale con lo spazio A₁O lineare (d).

Il primo caso (v < c) è semplicissimo. Lo mostra la Fig. 4.

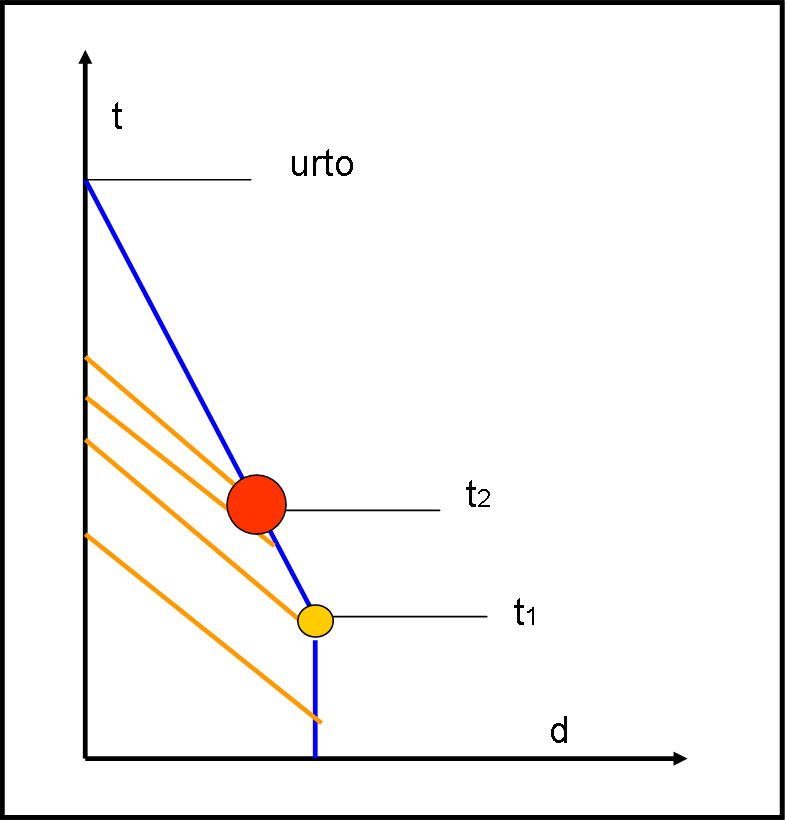
In azzurro vi è la linea di universo della stella, ossia il suo moto nello spaziotempo. All’inizio non si muove e quindi segue l’asse del tempo. In t₁ inizia il suo movimento con una certa velocità v minore della velocità della luce. Nello stesso istante parte la sua luce che raggiunge l’asse del tempo in cui si muove l’osservatore. La stella segue la sua evoluzione e diventa gigante in t₂. La luce emessa in questo istante non può che raggiungere l’osservatore in un tempo superiore a quello precedente. Gli intervalli di tempo dipendono dall’inclinazione della retta che indica il movimento della stella.

La Fig. 5 mostra il caso in cui la velocità della stella è proprio uguale a c.

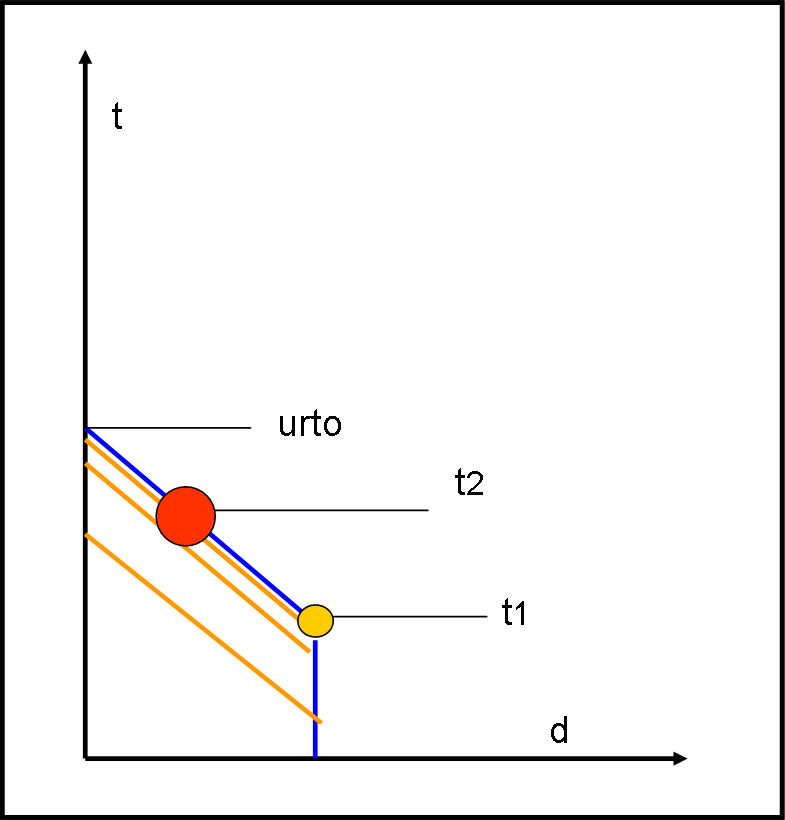
Prima di t₁, la luce raggiunge regolarmente l’osservatore. In t₁ la luce inizia il suo percorso, ma la stella non le è da meno e segue una retta a 45° come lei. Durante il tragitto della luce (e della stella) verso l’osservatore, l’astro diventa gigante. L’ultima immagine che l’osservatore riesce a vedere è quella che è partita poco prima di t₁. Quella partita da  t₁ arriva insieme alla stessa stella che causa la catastrofe. L’osservatore riesce ancora a vedere una stella come il Sole poco prima che sia partita da t₁, ma subito dopo viene impattato dall’astro.

La Fig. 6 mostra il caso in cui v > c.

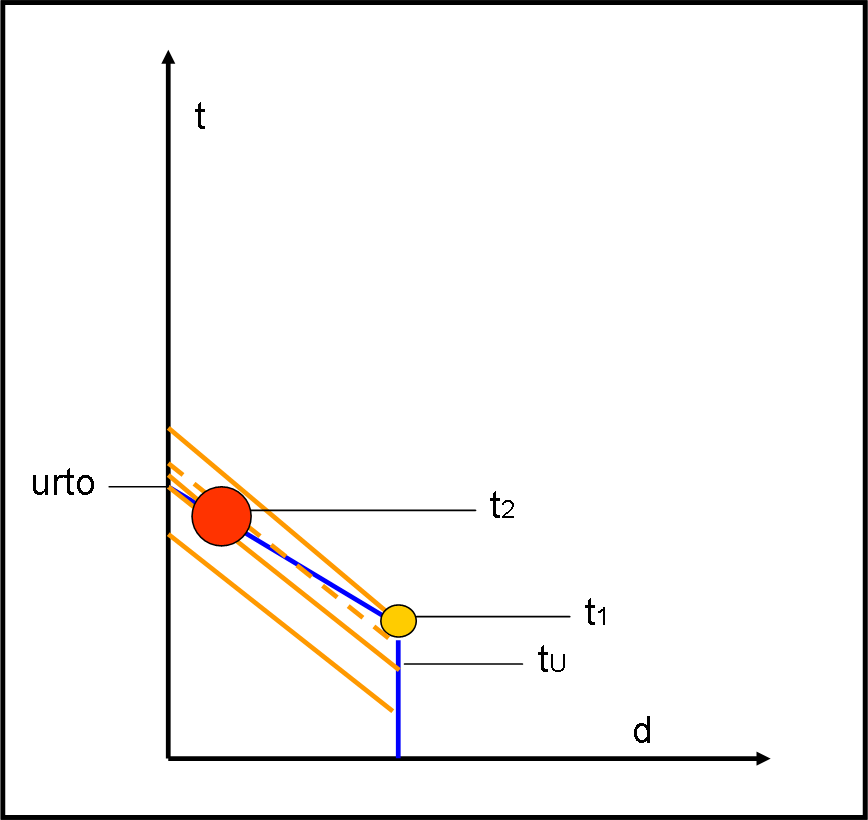
Prima che inizi il movimento della stella, giunge regolarmente la sua immagine. Poi, in t_1, non solo parte la luce, ma anche la stella che viaggia più veloce e che quindi arriva per prima all’osservatore. Se durante questo periodo di tempo a ipervelocità la stella si trasforma in gigante, sarà una gigante quella che piomberà addosso all’osservatore.

L’ultima luce stellare che giunge all’osservatore è quella partita in t_U. Dopo quell’istante la luce già partita  verso la sua destinazione viene raggiunta e superata dalla stella (linea tratteggiata). Questa luce arriva a destinazione dopo l’impatto, così come quella partita da t₁ e da t₂. Poco importa se quella di t₂ arriva prima di t₁… la catastrofe è già avvenuta e nessuno può più vedere qualcosa!

L’intera faccenda potrebbe essere ancora più complicata, pensando anche agli effetti di blueshift e anche peggio. Direi che per noi basta e avanza (non tentiamo, quindi, di aggiungere complicazioni ulteriori). In linea di massima i soliti “esperti” hanno risposto bene, tranne piccole imprecisioni qua e là. I muti sono rimasti muti… ma spero che questa spiegazione sia veramente alla portata di tutti, anche quando siamo partiti verso la fantascienza (Einstein ci perdoni!).