A volte si danno molte nozioni come acquisite. Poi ci si rende conto che quello che è ovvio per chi ha trafficato una vita con le posizioni di stelle e pianeti, proiettati sulla sfera celeste, potrebbe non essere così ovvio per molti altri. Tutti dobbiamo imparare qualcosa… e io per primo!

Pochi richiami estremamente banali, ma che reputo importante dare (i più esperti mi perdonino).

La sfera celeste è una sfera apparente, relativa a un certo osservatore, su cui vengono proiettati tutti i corpi che si vedono nel cielo. Il suo raggio può essere qualsiasi o, ancora meglio, è indeterminato. Ma poco importa, dato che le distanze tra gli astri (e così anche i diametri dei singoli oggetti) si misurano SOLO attraverso angoli, e quindi in gradi, primi e secondi (o in ore, minuti e secondi). Un angolo rimane se stesso a qualsiasi distanza.

Si può passare a distanze in km (o anni luce) solo quando si conosce la distanza rispetto all’osservatore. Prendiamo il caso del Sole. Pur non conoscendo la sua distanza da noi siamo sicuri (e possiamo misurarlo facilmente) che il suo diametro è, sulla nostra sfera celeste di circa ½ grado. In modo analogo possiamo dire che la distanza tra due stelle, visto da noi, è di X gradi o primi o secondi. Per potere passare alla effettiva distanza tra le stelle dobbiamo conoscere la loro distanza reale, A quel punto tutto si riduce alla soluzione di un triangolo.

Quando, invece, ci interessa ciò che appare sulla sfera celeste, siamo interessati solo e soltanto alla distanza apparente tra di loro misurata attraverso un angolo. Esso è sempre lo stesso, qualsiasi sia il raggio della sfera celeste che abbiamo scelto per fare un disegno esplicativo.

Ne segue che se conosciamo solo la distanza apparente sulla sfera celeste dobbiamo accontentarci di questa misura molto ambigua (anche se utilissima), che è poi quella che vediamo con gli occhi o con … stellarium. Senza osservazioni mirate, la vera distanza tra di loro rimane sconosciuta e così otteniamo le belle figure delle costellazioni che niente hanno, solitamente, a che fare con la realtà fisica.

La loro effettiva distanza rimane un mistero e ci accontentiamo di un angolo. Se, invece, conosciamo la distanza delle varie stelle è possibile fare il contrario e ricavare facilmente la posizione apparente sulla sfera celeste, dato che conosciamo lati e angoli dei giusti triangoli.

Per adesso non dico di più, altrimenti darei anche la soluzione del doppio quiz (QUI). Tuttavia, mi sono convinto e, spero che mi diate ragione, che sarebbe l’ora di saperci muovere sulla sfera celeste e, di conseguenza, fare conoscenza con la trigonometria sferica (da cui le varie coordinate come ascensione retta e declinazione; longitudine e latitudine; e via dicendo). Conoscere come muoversi ed eseguire misure su una superficie sferica, sarà senz’altro utile quando si parlerà di curvatura e di relatività generale. In astronomia tutto si intreccia e si lega strettamente…

Per dare una visione migliore di quello che ho cercato di spiegare a parole, inserisco la figura che segue e che cerco di spiegare nei dettagli, sperando che nel frattempo il nostro bravissimo Marko riesca a risolvere il problema delle formule e dei disegni da inserire nei commenti.

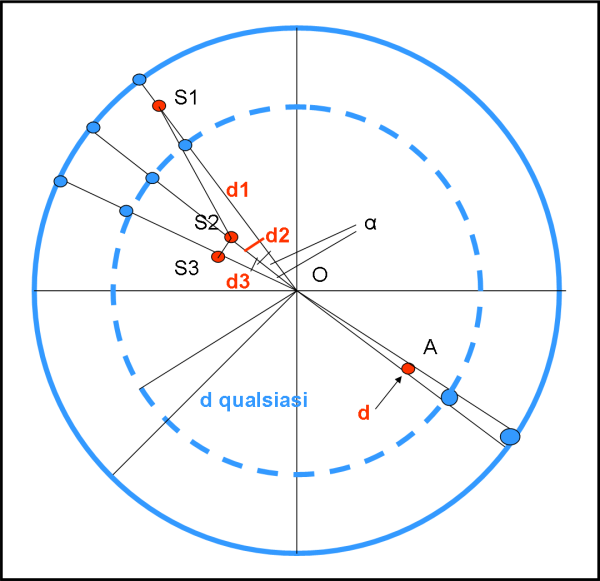
Prendiamo tre stelle reali S1, S2 e S3 (rosse) e analizziamo ciò che si vede da O e ciò che è, invece, la realtà fisica.

Le stelle hanno distanze ben diverse dall’osservatore (d1, d2 e d3). In particolare la distanza tra S1 e S2 è nettamente diversa da quella tra S2 e S3. Tuttavia, sulla sfera celeste le stelle si vedono come i cerchietti blu (sia sulla sfera celeste a linea intera che in quella tratteggiata e in qualsiasi altra volessi rappresentarle). L’angolo tra d1 e d2 e tra d2 e d3 risulta perfettamente uguale, ossia le stelle S1 e S3 sono, apparentemente, alla stessa distanza angolare da S2.

Cosa analoga capita per il diametro di A. Quello reale si può conoscere solo se si conosce la distanza A dall’osservatore, mentre quello apparente. o -meglio- angolare, rimane sempre lo stesso ovunque venga proiettato (l’angolo che lo sottende è sempre lo stesso).

Teniamo poi conto che un diametro stellare è talmente piccolo rispetto alla distanza, che considerare il suo seno o la sua tangente è praticamente la stessa cosa. Anzi il seno e la tangente possono anche essere considerati proprio come la misura dell’angolo in radianti.

Molte informazioni in più saranno date dopo che saranno giunte altre risposte, magari leggibili molto meglio, se i problemi informatici saranno risolti…

A presto…

QUI trovate la soluzione del quiz