Categorie: Astronomia Elementare Matematica Terra
Tags: angoli retti linee rette quiz viaggio terrestre
Scritto da: Vincenzo Zappalà
Commenti:34
Un viaggio troppo corto… oppure no? *
Questo è soltanto un gioco (se volete… chiamatelo pure un quiz) che serve come porta d’ingresso per il nuovo teatro astronomico che andremo a scoprire tra poco.
Parto dal punto A. Cammino lungo una retta fino a B. Poi svolto di un angolo retto e proseguo ancora dritto fino a C. Infine giro di altri 90 gradi e proseguo ritrovandomi al punto di partenza A.
No, non sto dando i numeri… ci riesco facilmente, anche se la Fig. 1 sembra dire di no. Eppure il viaggio è svolto proprio nel nostro mondo, sulla Terra! Chiunque potrebbe farlo…
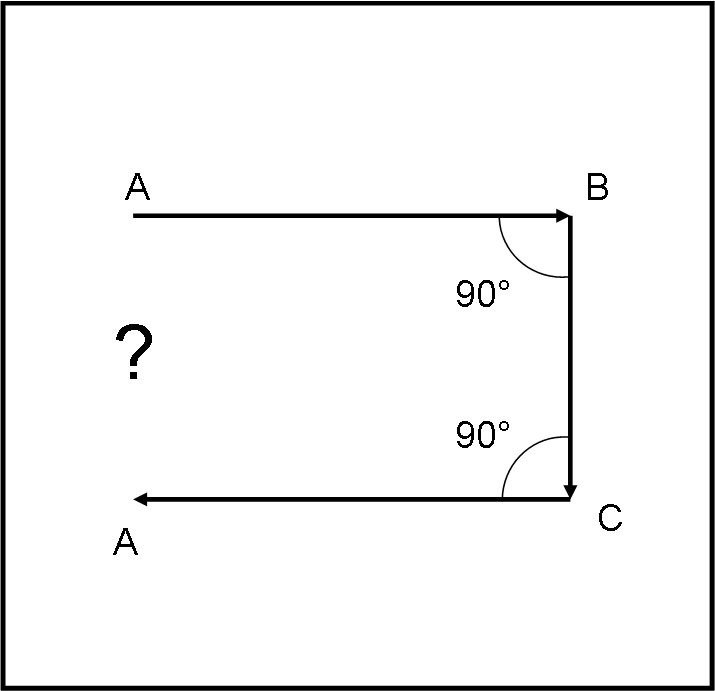
Vi sembra troppo corto? Dovrei camminare ancora un po'? Nemmeno per sogno, basta scegliere il giusto itinerario!
Ricordiamoci che una linea retta è una linea che non cambia mai direzione. Immaginate di usare una bici. Se vi sentite spostato un po’ a destra o un po’ a sinistra vuol dire che state curvando. Dovete sentirvi perfettamente verticale per essere sicuri di essere su una linea retta!
34 commenti
Sicuramente dall'alto della mia ignoranza dirò un'asinata....
Nella geometria sferica?
Traccio una riga sulla strada come per fare una gara,percorro come da disegno i due tratti di 90 gradi e sono di nuovo sulla linea di partenza .
Io ho realizzato una semplice figura terricola, però, per ora non posto nulla, poichè preferisco lasciar spazio ad altri... soprattutto i silenti... per cui avanti con le ipotesi.....
Paolo
Ho parlato di geometria sferica, perché ho pensato alla terra... I meridiani all'equatore formano angoli di 90% (se non erro) sono linee rette, e si ricongiungono ai poli
caro Gianni,
non fare il... furbetto
Ho parlato di punto di partenza e non di linea di partenza! 
Allora ha a che fare con la curvatura della terra e lo spazio piatto ,a sella o a curvatura positiva dove gli angoli non sono sempre Euclidei ma cambiano
Il punto A è uno dei poli. Siamo in geometria sferica e la somma degli angoli interni dei triangoli non è pi , è maggiore.
Il mio prof di Fisica 1 al politecnico aveva leggermente modificato la battuta: c'è un cacciatore di orsi che, dopo la passeggiata ad angolo retto, ne colpisce uno, dire di che colore è l'orso.
[Bianco]
Mah... a me sembra rosso
Paolo
e pensare che potrebbe essere retto anche l'ultimo angolo...
Non me ne ero accorto... attento Paolo! Ho detto che deve sempre andare in linea "retta". Il tuo cacciatore non lo fa sempre....
Volevo precisare che quello è l'orso e non il cacciatore... il primo mi è infinitamente più simpatico del secondo...
A parte ciò, caro Enzo la tua osservazione ha accentuato un mio dubbio...
Premetto che di geometria sferica non so nulla
, per cui posso solo fare alcune riflessioni da prendere con le pinze...
Nel disegno l'Orso rosso parte dal polo Nord, segue una linea longitudinale, ossia si dirige verso il Sud, poi svolta di 90° ossia si dirige verso est o verso ovest, mantiene la stessa latitudine per un po' di tempo, poi svolta di 90° verso il polo Nord e torna in A.
A me sembra che dal suo punto di vista ha seguito delle linee rette.
Visto dall'esterno (da un'astronave che orbita intorno alla Terra), soprattutto tra B e C, la linea che rappresenta la latitudine non è una retta, ma un arco di circonferenza.
Se taglio l'arco con una retta vista dall'esterno, l'orso varia la sua latitudine durante il percorso tra B e C.
Il problema è che una linea retta disegnata su un piano non è uguale a una linea dritta disegnata su una superficie curva.
Il rettilineo percorso dell'orso visto dall'esterno, non è rettilineo, ma assomiglia più a una curva, a un tratto di circonferenza..
Due linee parallele su un piano si incontrano solo all'infinito, ma due linee parallele su una superficie curva a me sembra che si possono incontrare in punto finito (il Polo Nord per esempio)...
Basta pensare alle distanze: una cosa è una retta che rappresenta il diametro del pianeta, altro è percorrere la linea equatoriale da un bordo all'altro del pianeta, ossia una semicirconferenza... il Diametro è una linea retta disegnata su un piano e vale due volte il raggio, mentre la linea equatoriale “corre” su una superficie curva... e metà circonferenza vale 3,14 volte in raggio del pianeta...
Come vedi il dubbio su come tracciare la linea retta tra B e C nasce da quanto esposto..
Paolo
Secondo me occorre partire dal polo, arrivare fino all'equatore, fare un pezzo di equatore (arco di cerchio massimo) e poi tornare al polo lungo un altro meridiano. In questo modo meridiani ed equatore sono cerchi massimi, quindi lungo di essi si andrà sempre in "linea retta"(sulla sup. sferica!).
Sono contento di aver cominciato la geometria sferica, sia per i risvolti puramente astronomici (sistemi di coordinate) sia per prendere dimestichezza con gli spazi curvi...
Caro Paolo, pensa alla definizione di retta nel piano: è una geodetica, ossia una linea di minimo percorso... La stessa cosa deve valere sulla sfera, ma...
E poi ci sono curve intrinseche (sono curve anche per chi vive sulla sfera) e curve estrinseche (sono curve solo per chi le vede da una dimensione in più)... Ricordate il famoso imbuto del buco nero....
Tutto si lega facilmente...
il percorso descritto dal quiz è quello illustrato nella seguente figura:
cioè, parto dal polo A camminando lungo un meridiano (una delle infinite circonferenze massime, che nella geometria sferica coincidono con le rette della geometria piana), arrivo in B posto sull'equatore, svolto di 90 gradi , percorrendo quindi un tratto di equatore (anche esso circonferenza massima, quindi "retta" nella geometria sferica), arrivo in C e svolto di 90 gradi riprendendo a camminare lungo un altro meridiano e tornando alla fine nel polo A.
Se, invece, nel primo tratto del percorso, mi fermassi prima di arrivare all'equatore e svoltassi di 90 gradi, non mi muoverei lungo una "retta" della geometria sferica (cioè circonferenze massime) , come evidenzia la seguente figura:
il percorso B-C in questo caso sarebbe quello di colore ciano, mentre quello di minima lunghezza (tratto di circonferenza massima) sarebbe quello di colore giallo. Quest'ultimo ottenuto sezionando la sfera con un piano passante per B, C e il centro della sfera.
benissimo Arturo! potrei fare a meno di scrivere la seconda puntata...
Scrivi, scrivi...!
La spiegazione e la figura di Arturo sono chiarissime, ma intuitivamente faccio fatica a prendere atto che il minimo percorso sia l'arco di circonferenza tra i due punti sull'equatore e non la corda che li unisce (come nel caso di un parallelo qualsiasi)!
cara Dany,
pensa di essere esattamente sull'equatore visto di taglio. Un arco equatoriale lo vedi come un segmento di retta. Qualsiasi altra linea che congiunge gli estremi è una curva sicuramente più lunga. Ogni cerchio massimo è come se fosse l'equatore....
Comunque, sarà dimostrato nella prima puntata....
Ottimo! Perchè, per quanto mi impegni, non riesco a 'visualizzare' la differenza tra l'equatore e un qualunque altro parallelo...
Dany io ho commesso lo stesso errore...
La figura di Arturo mi sembra esaustiva, io ne ho realizzato un'altra proprio per evidenziare perché il percorso più breve tra B e C non corrisponde alla linea della latitudine (paralleli)...
Si tratta di una visione dall'esterno.... magari puà essere utile per "visualizzare"...
Nella figura a sinistra le ellissi azzurre orizzontali rappresentano i paralleli, mentre l'ellisse viola passa per il centro della sfera e per i punti B e C.
Il tragitto più breve tra B e C è quello rosso che segue proprio la sfera tagliata dall'ellisse viola, mentre il tragitto giallo che segue l'ellisse azzurra (latitudine) è più lungo.
Ciò è ancora più evidente ruotando tutto....come nella figura a destra.
E' evidente che nella seconda figura il percorso giallo tra B e C è più lungo di quello rosso....
D'altronde all'equatore il percorso più breve è proprio quello che segue la linea equatoriale...
L'equatore in realtà è il cerchio massimo di una sfera, se ruoti una sfera il cerchio massimo non può certo cambiare misura...
Ora penso e spero di aver capito..
Paolo
In attesa delle successive puntate di Vincenzo sulla geometria sferica, provo a dare una prova analitica del fatto che la distanza BC misurata lungo un parallelo che non sia l'equatore è maggiore della distanza BC misurata lungo la circonferenza massima passante per tali due punti della sfera.
Con riferimento alle figure che avevo già pubblicato, per semplicità nascondo alla vista la superficie della sfera e dei piani con cui l'avevo sezionata, lasciando visibile solo cio' che ci interessa in questa sede. La figura è ora la seguente:
la circonferenza di colore ciano è quella ottenuta sezionando la sfera con un piano parallelo a quello equatoriale ma a latitudine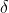
. La circonferenza gialla è invece quella massima, ottenuta sezionando la sfera con un piano passante per gli stessi due punti B e C, ma anche per il centro O della sfera.
Indico con
l'angolo BKC e con 
l'angolo BOC. Angoli misurati in gradi. Fissato 
, l'angolo 
diminuisce man mano che ci spostiamo verso il polo , cioè man mano che aumenta la latitudine del parallelo congiungente i punti B e C.
La lunghezza dell'arco BC è data da:
Devo dimostrare che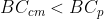
. Ci provo.
Considero il triangolo KBC. Esso è isoscele, per avere due lati pari al raggio r della circonferenza di colore ciano. Per le proprietà dei triangoli isosceli, l'altezza KH, che ho chiamato "a" nella figura, relativa alla base BC è data, quindi, da:
Considero ora il triangolo OBC. Anche esso è isoscele, per avere due lati pari al raggio R della sfera. Anche per esso, quindi, l'altezza OH, che ho chiamato "b" nella figura, relativa alla base base BC (che coincide con quella del precedente triangolo) è data da:
Considero ora il triangolo KBO. Esso è rettangolo in K. Posso, quindi, trovare il cateto KO con il teorema di Pitagora:
Inoltre, per i teoremi di trigonometria piana sui triangoli rettangoli, è anche:
Considero, infine, il triangolo KHO. Anche esso è rettangolo in K. Per il teorema di Pitagora avrò:
Confrontando la (5) e la (7) ottengo:
sostituendo nella (8) le espressioni a a e b ottenute dalle (3) e (4) si ha:
da cui, dopo alcuni passaggi, si ricava:
e, per la (6):
quindi:
Attraverso la (9) e con le (1) e (2) posso ricavarmi , fissati i valori di
e di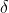 
, il rapporto tra le lunghezze di 
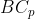e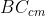 
. In ogni caso risulterà 
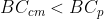. Per esempio, poniamo:
risulta dalla (9):
quindi, dalle (1) e (2), rammentando la (6):
da cui:
Fissato
, per qualsiasi valore di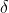 
ottengo sempre una lunghezza di 
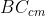minore di quella di 
.
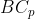Quantitativamente, la differenza non è molto grande. Sapendo che il raggio terrestre è di circa 6370 km, con i suddetti valori di latitudine e distanza angolare tra i due meridiani, quello passante per B e quello passante per C, ottengo
con una differenza di cammino di 382 km circa. La massima differenza, sempre per distanza angolare di 90 gradi tra i meridiani, si ha per una latitudine di circa 52 gradi, ed è pari a circa 446 km. Differenze maggiori si hanno con maggiori distanze angolari tra i meridiani.
Ho capito cosa avevo frainteso nel disegno di Arturo e sono pronta per la seconda puntata... grazie Paolo!
Come ulteriore ausilio , stavolta grafico, per convincersi che l'arco BC di circonferenza massima è quello di lunghezza minore, ho realizzato con Geogebra un modello di geometria solida del problema, nel quale i due punti B e C hanno le loro terne di coordinate spaziali x, y e z (funzione delle loro corrispondenti coordinate polari) che soddisfano l'equazione della sfera di raggio R e con centro nell'origine del sistema di riferimento. La retta passante per B e C è quella di sostegno del fascio proprio di piani (l'equivalente del fascio proprio di rette nella geometria piana). Ciascuno di tali piani va a sezionare la sfera secondo una circonferenza, il cui centro D è indicato con il punto grosso nel grafico. Tutti i piani di tale fascio sono individuati al variare del parametro k. Agendo, quindi, sul cursore del parametro k, è possibile vedere ruotare il generico piano del fascio attorno alla retta BC e visualizzare la relativa circonferenza di intersezione con la sfera. In particolare, ho evidenziato l'arco BC di tale circonferenza , di cui l'applicazione calcola automaticamente la lunghezza. Variando k, quindi, cioè variando il piano di sezione, si vede variare la lunghezza dell'arco BC. Si può constatare che, effettivamente, con i dati di partenza che avevo indicato nel precedente commento, si la la minima lunghezza (1,05 R) quando il centro della circonferenza di sezione va a coincidere con il centro della sfera. Mentre se prendiamo il k a cui corrisponde un piano passante per B e C e parallelo a quello equatoriale, si ha come lunghezza dell'arco BC quello trovato nel precedente commento, cioè 1,11 R.
Questo link per smanettare online con il modello da me realizzato:
http://www.geogebra.org/m/RSw3nNr8
(funziona di sicuro con Internet Explorer e con Google Chrome, con gli altri browsers non saprei)
Lungi dall'essere un software "pappa pronta", Geogebra è un potenze ausilio per lo studio di problemi di geometria analitica, anche solida, come in questo caso. Sicuramente molti di voi lo conoscono già.
Conosco Geogebra perchè lo utilizza con molta scioltezza mia figlia (terza liceo) ed è praticamente inpossibile usarlo se non si ha una perfetta cognizione di causa di ciò che si vuole disegnare e degli strumenti matematici che servono allo scopo... io, infatti, ci ho litigato per un paio d'ore e mi sono arresa
! Ma prima o poi lo riaffronterò!!
Sicuramente sì, non lo metto in discussione. Comunque, non c'è bisogno di andare per tentativi grafici... basta il ragionamento e la definizione di retta e di curvatura... come penso di aver dimostrato nella seconda parte. Dopo di che, si può benissimo utilizzare un qualsiasi sistema grafico anche di alta raffinatezza.
Se poi si passa alla visione estrinseca tutto diventa immediato e la costruzione da eseguire è proprio simile a quella utilizzata dal programma. Come diciamo sempre, la mente e un semplice disegnino approssimativo (ricordiamoci la cupola del Brunelleschi) risolve il problema. poi si possono usare tutti i metodi più sofisticati per la rappresentazione o per la costruzione della cupola (Brunelleschi è però dovuto andare da solo per primo, sul tamburo dato che gli operai non credevano a idee schizzate sulla sabbia...
).
Comunque, ne parleremo ancora nel terzo capitolo
Io per dire la verità mi ci sono fiondato (su geogebra) perché mi ero messo a impostare un discorso analitico generale, con un problema di minimo della funzione "lunghezza dell'arco BC" al variare del piano con cui seziono la sfera. Cioè, mi sarebbe piaciuto arrivare a dimostrare per via analitica che il piano passante per i due punti e per il centro della sfera è quello per cui si ha la lunghezza minima del percorso tra B e C. Ma si è rivelato un procedimento da perderci la testa , visto che la generica circonferenza di intersezione tra piano e sfera è inclinata rispetto a due dei tre piani di riferimento... un macello
. Per cui alla fine ho ripiegato su Geogebra. Naturalmente, avanti tutta con gli articoli sulla geometria sferica 
ne ero certo Arturo. Comunque non c'è bisogno di usare una rappresentazione a tre dimensioni. Ogni piano determina una circonferenza che passa per due punti stabiliti (basta fare girare il piano con asse la retta per i due punti). Ogni piano ha quindi una soluzione su due dimensioni. Quando hai fatto girare il piano di 36o° hai tante circonferenze che stanno su piani diversi, ma che mantengono le unità di misura. Ne segue che puoi considerarle tutte su un singolo piano e il problema diventa a due sole dimensioni...
Alla fine ci sono riuscito. Ho aggirato l'ostacolo della complicazione analitica utilizzando la proprietà geometria secondo cui un piano generico, passante per due punti apparteneneti ad una sfera e che quindi seziona la sfera secondo una circonferenza è sempre perpendicolare, per la simmetria spaziale della sfera, alla congiungente il centro della sfera con il centro della circonferenza ottenuta dalla sezione. In questo modo, posso ricavarmi il raggio di tale circonferenza, che poi è ciò che mi serve per calcolare la lunghezza dell'arco BC, semplicemente con il teorema di Pitagora, noto il raggio R della sfera e la distanza OD (tra il centro della sfera e il centro della circonferenza di sezione). Alla fine ho ottenuto una espressione della lunghezza dell'arco BC funzione del parametro k al variare del quale varia il piano con cui seziono la sfera , e dunque la circonferenza che ottengo dalla sezione. Studio tale funzione e trovo che il valore di k per cui l'arco BC ha lunghezza minima è effettivamente quello in corrispondenza del quale il relativo piano passa per il centro della sfera, quindi la circonferenza di sezione è effettivamente una circonferenza massima
Ometto i passaggi, a meno che non interessino, perché, comunque, l'espressione trovata per la lunghezza dell'arco BC in funzione di k è abbastanza complicata (la variabile k compare al quadrato, al denominatore, sotto radice quadrata e in un arcoseno...)
Ah, San Tommaso aveva più fede...
Ne ero sicuro Arturo...
senti, perché non mi mandi la tua trattazione, messa giù per bene, e la inseriamo come appendice (a tuo nome) nella terza puntata della curvatura? Questo sì che è lavoro di gruppo!!!!
Il mio email lo trovi nei contatti...
Ci conto, eh...
Scusate.
Vincenzo, non riesco a vedere il tuo indirizzo email nella sezione "Contatti". Ho inviato un msg con l'apposito form ma non sono sicuro che sia arrivato a destinazione.
caro Arturo,
ti mando un msg dal mio email, così avrai subito l'indirizzo personale...
Dunque se ci sono tre lati si tratta di un triangolo?
se si allora si ha che la somma degli angoli interni supera l'angolo piatto!
ovviamente Gianni :-)