Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Siamo quasi pronti per dimostrare la non numerabilità dell'insieme dei numeri reali. Purtroppo senza alcune proprietà della continuità di R, non è possibile darne un dimostrazione convincente. Di solito si fa in quattro righe sfruttando la notazione decimale dei numeri reali e il secondo metodo diagonale di Cantor; a parte il fatto che la notazione decimale comporta alcuni problemi di non univocità , essa non è una delle cose più semplici da giustificare a fondo e inoltre deriva sempre dalle costruzioni di Dedekind e quindi dall'assioma di continuità. Vi chiedo quindi ancora un po' di pazienza. L'idea che ebbe Cantor può essere illustrata in un altro modo, che non è poi diversa da quella che usa la notazione decimale dei numeri reali, e fu quella di suddividere un intervallo dei numeri reali  con un procedimento ricorsivo in intervalli tali che ogni intervallo contenga il successivo, ed escludendo dei numeri naturali, appartenenti a certe successioni. Vi premetto questo per cercare di convincervi  che non stiamo faticando a vuoto.

Adesso che abbiamo a disposizione l'assioma di completezza, possiamo dimostrare un fatto importante ed anche simpatico riguardo a tali intervalli, che ci permetterà di  dimostrare la non numerabilità di R in modo quasi immediato. Prendiamo in considerazione  una successione infinita di intervalli chiusi    per ogni n e di lunghezza sempre più piccola (l'estremo inferiore delle lunghezze è uguale a zero, ovvero esistono intervalli di larghezza minore a e  e qualsiasi sia e >0)

Si ha quindi;

cosa sarà intuitivamente l'intersezione di tutti questi intervalli ?   Un solo punto. Scopo di questo articolo sarà dimostrare proprio questo partendo dall'assioma di continuità. Prima una definizione e un teorema.

Coppie separate

Una coppia (A,B) di sottoinsiemi non vuoti di R si dice separata se per ogni
a in A e b in B si ha a<= b. Un numero reale x si dice un elemento di separazione della coppia (A,B) se a<=x <= b per ogni a in A e b in B.

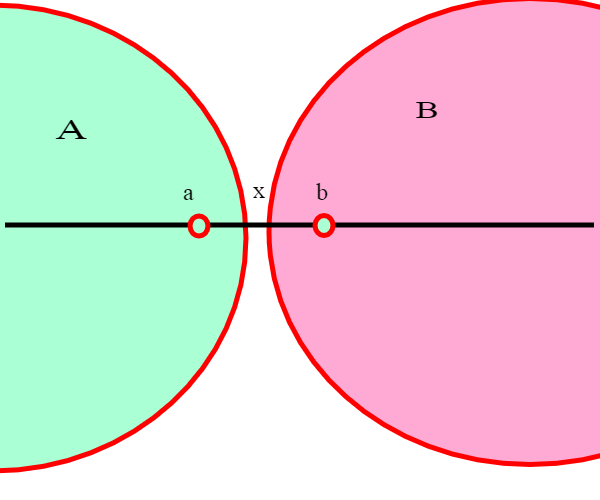
Una coppia separata si dice contigua se per ogni numero reale e > 0 esistono due elementi a in A e b in B tali che b − a <e .

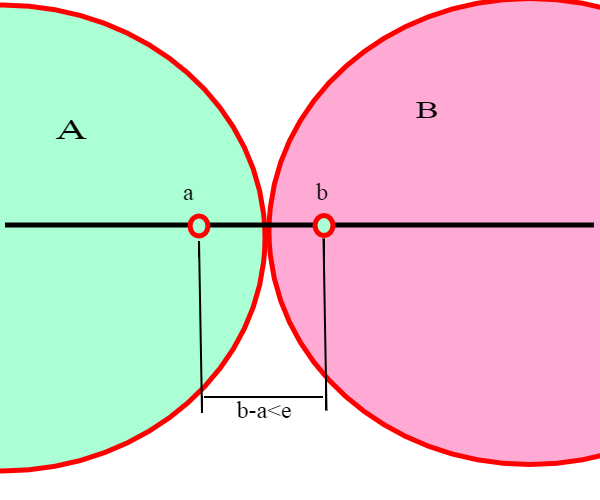
Ma esisterà sempre un elemento separatore che sta in mezzo? Si , grazie all'assioma di continuità.

Se (A,B) è  una coppia separata di sottoinsiemi non vuoti di R esiste almeno
un elemento di separazione. Se la coppia è contigua l’elemento di separazione è unico.

Ogni elemento di B è un maggiorante di A. Quindi A è superiormente limitato e, per l’assioma di completezza, esiste supA. Poichè supA è il minimo dei maggioranti di A, si ha supA <= b per ogni b appartenente a B. Quindi supA è un minorante di B e pertanto supA <= inf B essendo inf B il massimo dei minoranti. Tutti gli elementi dell’intervallo [supA, inf B] sono elementi di separazione della coppia (A,B) per la definizione di intervallo.

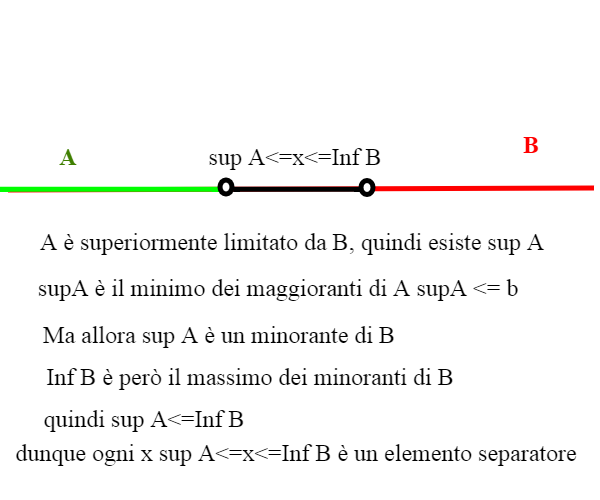
Prendiamo come esempio A={a<1/2} , {b>1}, a e b appartenenti ad R. Ogni elemento di a è minore di ogni elemento di b ; supA=1/2, inf B=1, tutti gli x appartenenti all'intervallo [1/2,1] sono elementi separatori.

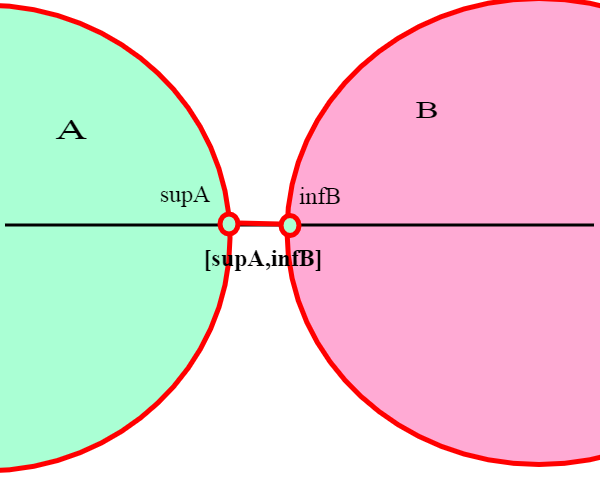
Supponiamo ora che (A,B) sia contigua. Osserviamo che se x è un elemento di separazione allora deve essere supA<= x<= inf B. Per dimostrare che l'elemento di separazione è unico, basta provare che :

supA = inf B.

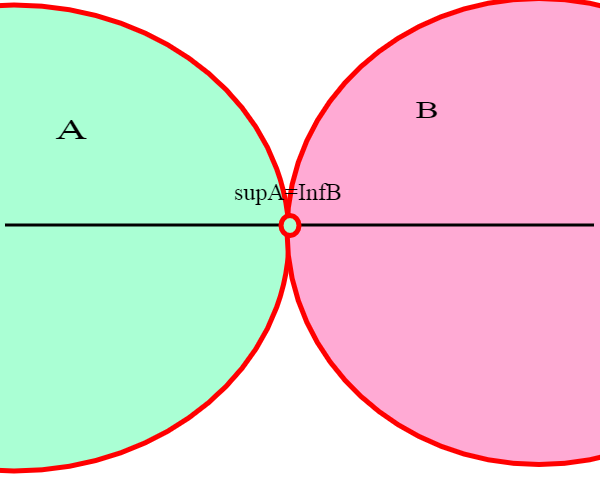
Guardiamo il disegno sopra: se supA < inf B, allora la differenza è maggiore di zero:posto e = inf B −supA, per la definizione di contiguità dovrebbero esistere due elementi a, b il primo in A e il secondo in B con differenza b-a<e; ma questo non è possibile, come si vede dal disegno. Infatti:

a<=sup A<=inf B  <=b, pertanto b-a>inf B-sup A.  Quindi sup A non può essere strettamente minore di inf B. Ma allora supA = inf B.

Le dimostrazioni per assurdo lasciano sempre un po' di amaro in bocca, e io cerco di evitarle, perchè a volte possono generare confusione. Possiamo anche pensarla in altro modo; se fra sup A e inf B ci sono degli elementi di R,  non tutti  appartengono  ad A o  B. Si genera in tal modo un ostruzione alla contiguità; non posso avvicinarmi indefinitamente alle alle due classi separate.

Esempio:A={a<=0, a numero reale}, B={1/n , n numero naturale ,n>0}. ogni elemento di a è minore di ogni elemento di b; A e B sono contigue;  infatti qualsiasi sia e>0, troviamo a=0 , b=1/n con n>1/e; a è in A e B è in B   ma allora sup A=0, Inf B=0

Ma chi mi assicura che qualsiasi sia e, riusciamo a trovare un n abbastanza grande affinché n>1/e ? L'assioma di Archimede! (quindi pensate quanti anni ha l'assioma). Al tempo, quando Archimede per primo lo formulò era un assioma, oggi possiamo giustificarlo con quello che abbiamo visto su R.

Comunque si scelgano due numeri e, a positivi esiste un numero naturale tale che n*e>a.

(nel nostro esempio  a=1).Giustifichiamolo inizialmente così .  Se ad esempio a=1, e=0,00000003

1/e=33333333,333333333333333333333333..  basta prendere n > 33333333 +1 (ho considerato la parte intera di 1/e, e ho aggiunto 1. La dimostrazione rigorosa l'ho messa in appendice a questo articolo, per chi vuole approfondire.

Gli intervalli incapsulati

Torniamo ora agli intervalli di cui abbiamo parlato all'inizio.
Una successione di intervalli (In) si dice incapsulata se In  per ogni n
Si ha quindi 

l’intersezione di una successione incapsulata di intervalli chiusi e limitati non è mai vuota.
Se (In) è una successione  di intervalli chiusi e limitati incapsulati esiste un elemento comune a tutti gli intervalli.

Tale elemento è  unico se l’estremo inferiore delle lunghezze degli intervalli è 0. (per chi conosce l'analisi matematica si può anche dire che )

Sia In = [an, bn]. La lunghezza di In è allora l(In) = bn −an . Consideriamo gli insiemi A = {an : n in N} e B = {bn : n in N}. Dimostriamo che la coppia (A,B) è separata.

Si ha che an <= bn per ogni n, perchè an e bn sono, rispettivamente, primo e secondo estremo dello stesso intervallo. Questo però non ci basta, dobbiamo dimostrare che qualsiasi sia h,k ak<=bh (qualsiasi a in A deve essere minore uguale di qualsiasi b in B).

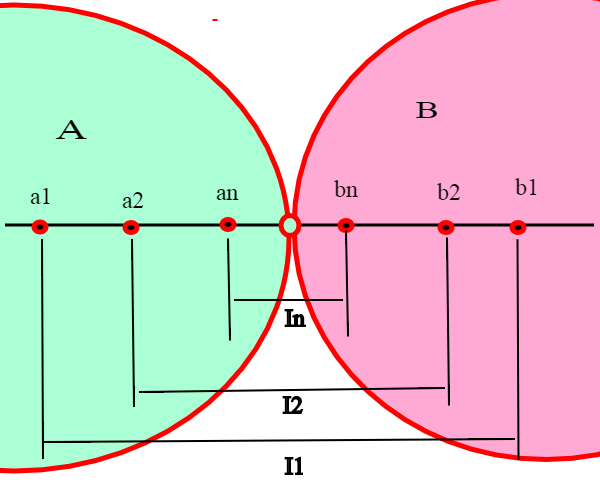
Sia n <= m; allora poichè Im è contenuto in  In si ha che an <= am
e bm <= bn . Guardiamo il disegno,:1<2, I2 è contenuto in I1, a1<a2, b1>b2. Siano ora  un generico elemento di A e  un generico elemento di B (facciamo variare cioè gli indici h,k in tutti i modi possibili)

Ci sono due possibilità:
se k <= h si ha

se h<=k si ha  

In ogni caso    e, quindi, (A,B) è separata .Ma abbiamo visto sopra  che:

Se (A,B) è  una coppia separata di sottoinsiemi non vuoti di R esiste almeno
un elemento di separazione. 

esiste quindi un numero reale x tale che an <= x <= bn per ogni n. Pertanto x appartiene a  In per ogni n.

Sappiamo ora che l'estremo inferiore delle lunghezze egli intervalli è zero:

inf{l(In) :n in N} = 0; se ricordiamo quanto detto nell'articolo precedente, questo significa che qualsiasi sai e>0, troviamo un n tale che l(In)<e. ma l(In)=bn-an, quindi per un certo n, abbiamo due elementi, an e bn in A e B tali che bn-an<e; ma questa è la definizione di classe contigua.

Se la coppia è contigua l’elemento di separazione è unico.

Riassumendo: esiste  un numero reale x tale che an <= x <= bn per ogni n, quindi x appartiene ad ogni In, e quindi alla'intersezione , in più x è unico.

Appendice

L'assioma di Archimede

Comunque si scelgano due numeri e, a reali positivi esiste un numero naturale n tale che n*e>a.

Supponiamo che questo non sia vero; allora dati e, a n*e<a per ogni numero naturale n; ma allora a è un maggiorante dell' insieme A={n*e, n appartenente a N}, quindi a è superiormente limitato. Per l'assioma di continuità, esiste l'estremo superiore sup A. Quindi  n*e <=sup A qualsiasi sia n. Prendiamo m=n+1;

m*e<=a, (n+1)*e<a, n*e <=sup a-e che quindi diventa un maggiorante di A ;ma sup A-e <sup A contrariamente al fatto che sup A sia il minimo dei maggioranti.

Articoli precedenti:

Cantor parte nona; La continuità di R

Cantori, parte ottava;L'insieme delle parti e il teorema di Cantor

Cantor, parte settima La numerabilità di Q

Cantor, parte sesta:Il minimo ordine di infinito

Cantor pare quinta,Il principio di induzione

Cantor, parte quarta. L'abergo di Cantor

CANTOR parte Terza, gli insiemi numerabili

CANTOR parte Seconda: Corrispondenze e funzioni

CANTOR parte prima, gli insiemi

 

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica