Categorie: Astronomia Elementare Matematica
Tags: angoli sferici geometria non euclidea geometria sferica quiz rette parallele sfera celeste soluzione triangolo sferico
Scritto da: Vincenzo Zappalà
Commenti:17
DOPPIO QUIZ. Curviamo il mondo. 4: dopo i lati, gli angoli **
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Definiti i lati di un triangolo sferico, non ci resta che definire quali siano i suoi angoli. Nel fare questo, risolviamo il vecchio quiz e stabiliamo anche un’altra proprietà molto interessante dei triangoli sferici. Concludiamo con due nuovi quiz, che saranno risolti la volta successiva.
Per un abitante della superficie sferica, il problema di definire un angolo sulla sua superficie non è certo irrisolvibile. Lui può girare su stesso fino a ritrovarsi nella stessa direzione di partenza. Questa azione gli dice di avere descritto un angolo di 360°. Può, perciò, valutare a quale rotazione corrisponde un grado. Tracciando due rette intrinseche è allora facile per lui calcolare quanti gradi sono contenuti in uno dei quattro angoli che le due rette definiscono, come rappresentato in Fig. 9, a sinistra.
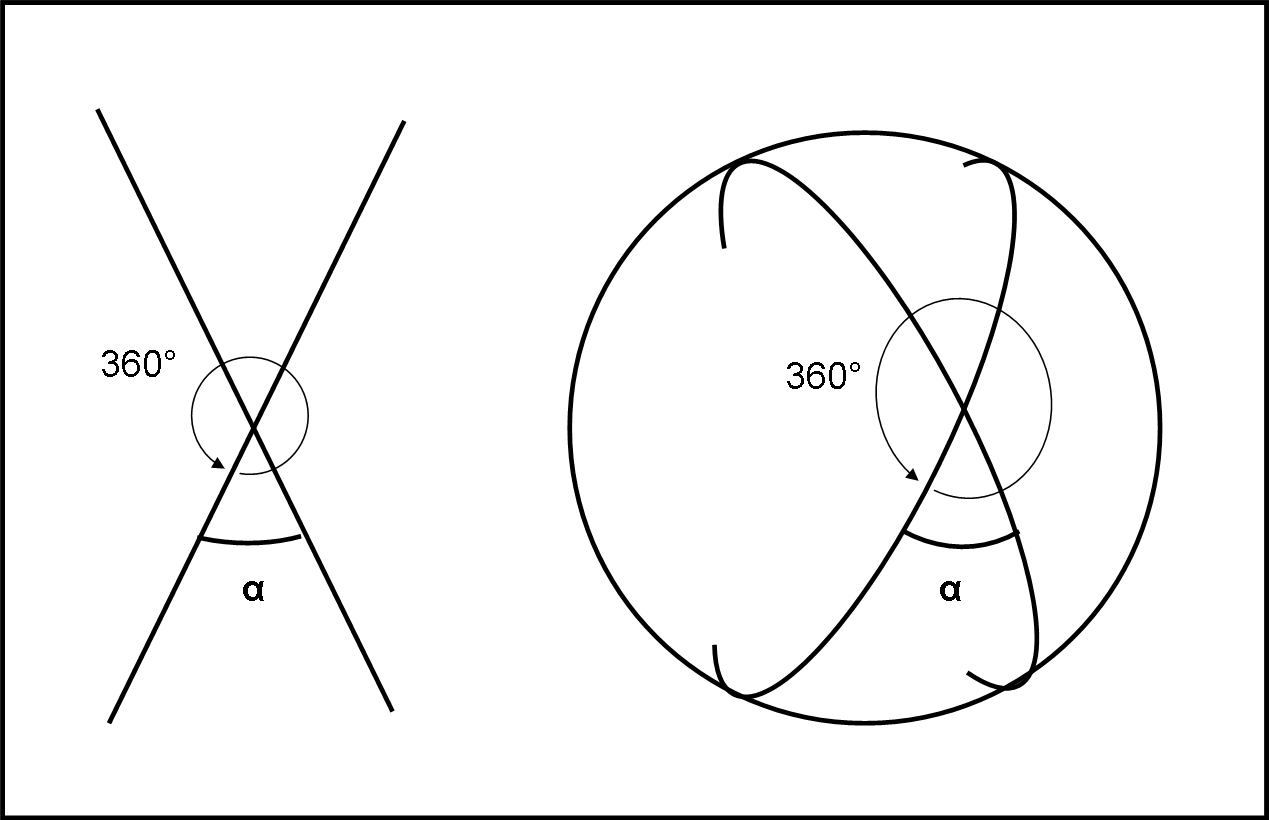
A destra della stessa figura, vediamo come questa descrizione intrinseca venga vista dal “di fuori” (visione estrinseca). Notiamo, ovviamente, che le rette non sono altro che cerchi massimi.
Per noi abitanti delle tre dimensioni, però, questo sistema per misurare gli angoli sulla superficie sferica diventa un po’ troppo macchinosa e, approfittando della nostra capacità di osservare dall’alto e di potere usare enti geometrici che gli abitanti di sferilandia non possono nemmeno intuire, possiamo definire gli angoli sferici in modo molto più immediato e utile per i futuri calcoli, così come abbiamo fatto per gli archi di cerchio massimo (ossia i lati intrinsechi).
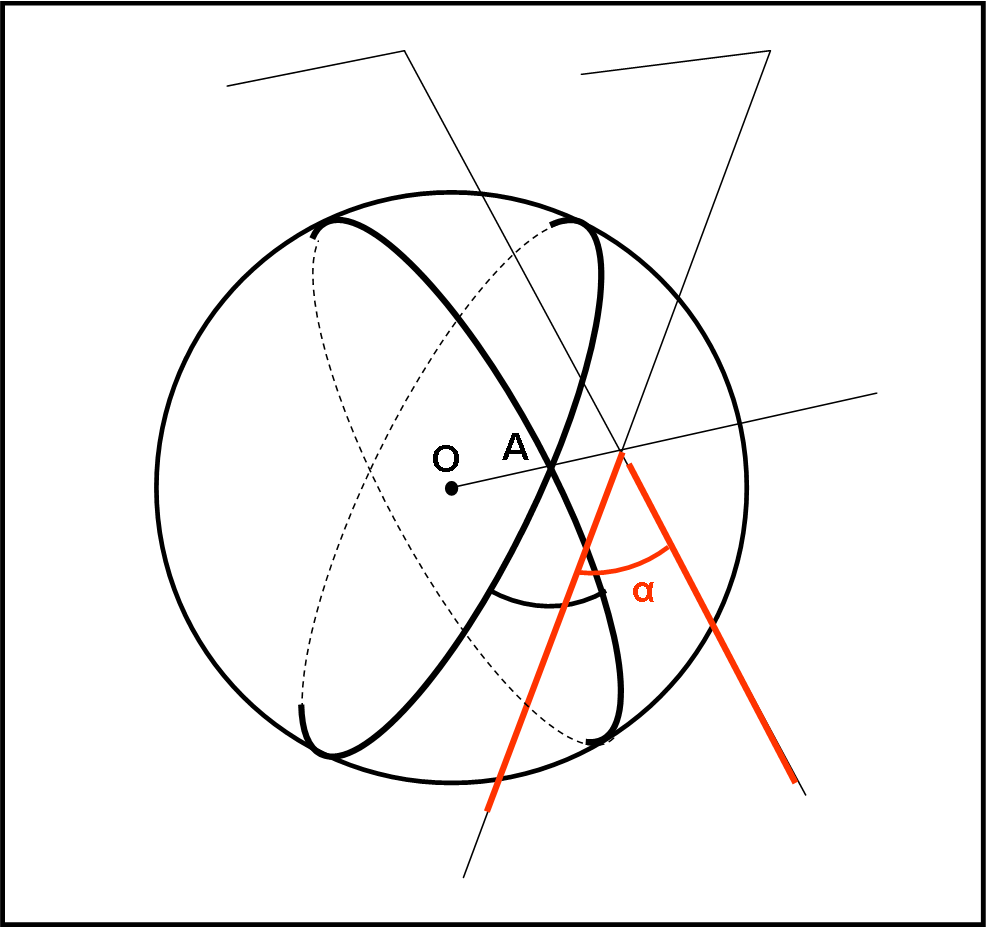
Sappiamo perfettamente che un angolo sferico deve essere compreso tra due cerchi massimi, che si ottengono tagliando la sfera con due piani. Basta allora definire come angolo sferico l’angolo formato dalle tangenti ai due cerchi massimi nel vertice considerato. Sostituiamo, all’angolo misurato sulla superficie, un angolo compreso tra dure rette vere e proprie dello spazio tridimensionale. Vediamo la semplice costruzione nella Fig. 10.
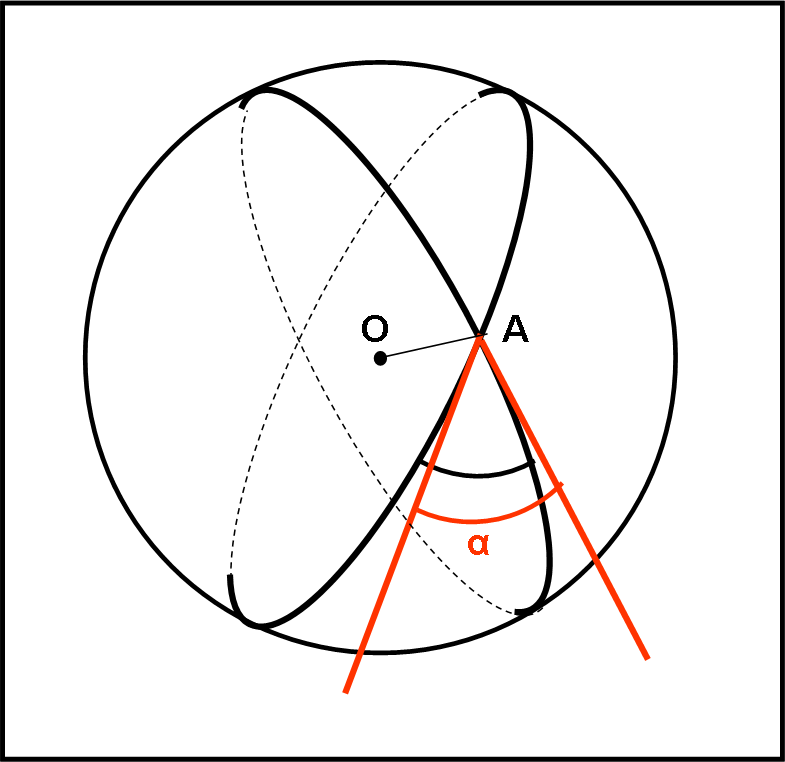
Utilizziamo anche un’altra definizione. Anche se non abbiamo ancora trattato la geometria tridimensionale e i suoi abitanti, come piani, sfere, rette, ecc. (lo sta facendo Arturo, QUI), possiamo facilmente definire un angolo tra due piani, chiamato angolo diedro. Esso esiste sempre quando i piani non sono paralleli e, quindi si incontrano lungo una retta. Bene, l’angolo diedro è quello formato da due rette perpendicolari alla retta comune e appartenenti ai due piani, come mostra la Fig. 11.
O, se preferite, possiamo considerare un terzo piano perpendicolare alla retta comune e definire come angolo diedro l’angolo formato dalle due rette intersezione di questo piano con quelli originali. L’angolo sferico è proprio l’angolo diedro tra i due piani contenenti i due cerchi massimi. Se ci riflettiamo un attimo ci accorgiamo di aver detto la stessa cosa con parole diverse.
Scegliendo la definizione che preferiamo (io penso sia meglio parlare di tangenti ai cerchi massimi, che, come tali devono appartenere ai piani dei cerchi massimi), si è facilmente risolta anche la questione degli angoli. Siamo ora in grado di lavorare con i triangoli sferici, conoscendo perfettamente i parametri che li caratterizzano. Parametri che, in qualche modo, si rifanno sempre al centro della sfera. In altre parole, dopo aver conosciuto e compreso la visione intrinseca, lavoriamo, d’ora in poi, solo con la visione estrinseca, decisamente più facile.
Ah… come sarebbe bello fare lo stesso con uno spazio a tre dimensioni o con uno spaziotempo a quattro dimensioni!
Accontentiamoci e prepariamoci psicologicamente a divertirci con le funzioni trigonometriche.
Qualcuno potrebbe dire: “Accidenti, andava tanto bene così… senza formule…”. Purtroppo, per introdurre le coordinate sferiche e i passaggi da un sistema all’altro abbiamo bisogno di legare tra loro i vari parametri e questo si può fare solo con le funzioni trigonometriche. Forza e coraggio… non ce ne pentiremo!
Prima di andare avanti, però, è giusto dare la risposta al quiz (QUI) che aspetta una risposta da tanto tempo. E’ ormai chiaro che per potere tornare al punto di partenza, con due sole deviazioni di 90°, non possiamo che essere su una superficie sferica. Tuttavia, abbiamo anche capito che dobbiamo muoverci lungo i lati di un triangolo sferico, trascurando qualsiasi curva intrinseca che sembrerebbe utilizzabile. Se è curva intrinseca non avremmo più un percorso lungo segmenti rettilinei!
Disegniamo la Fig. 12, che spiega tutto e che ci fa conoscere un’altra caratteristica fondamentale dei triangoli sferici.
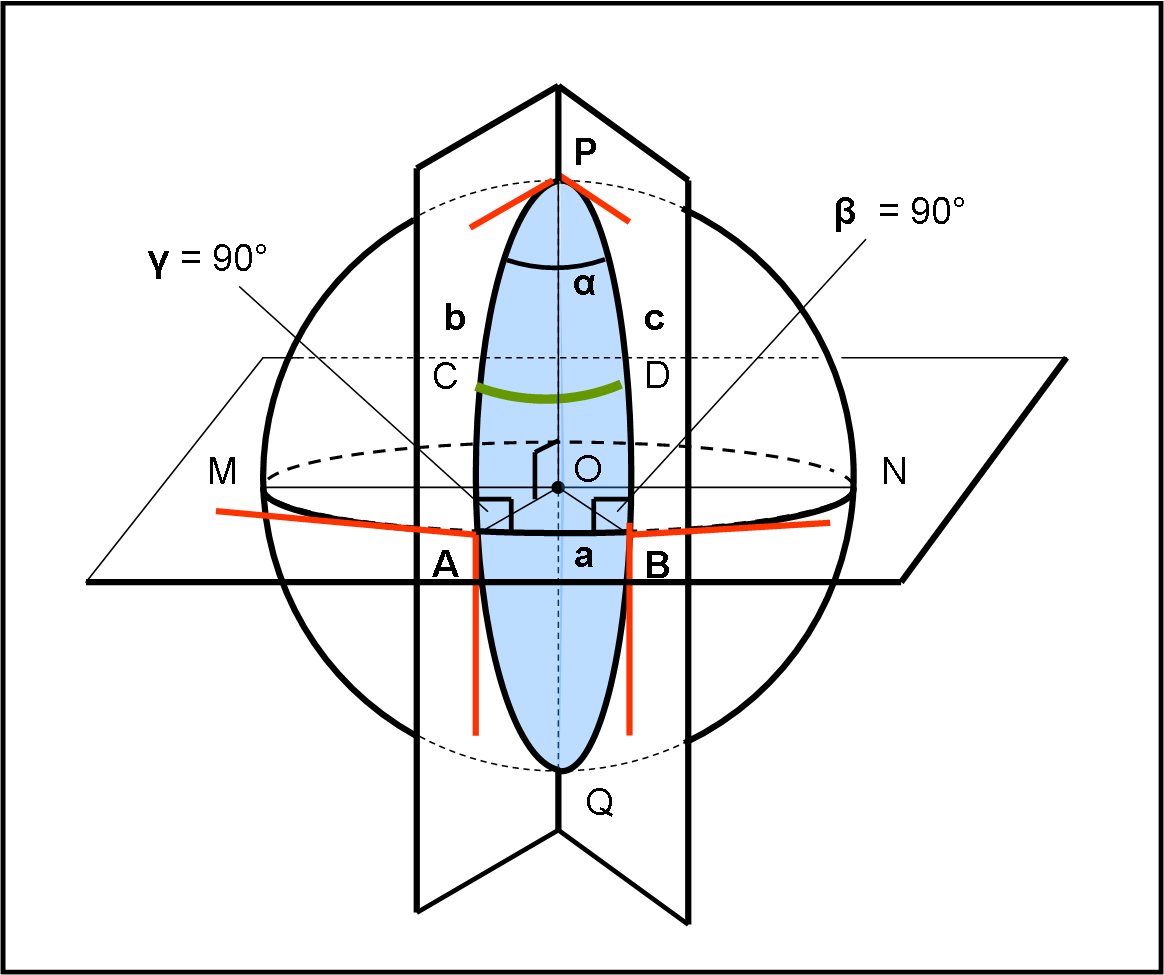
Consideriamo un piano qualsiasi passante per il centro O della sfera e il cerchio massimo da lui determinato. Questo cerchio massimo lo mettiamo “in orizzontale” (chiamiamolo, per adesso, proprio piano orizzontale) ed è individuato dai punti MABN. Tracciamo dal centro O la retta perpendicolare al piano: questa interseca la superficie sferica in punto P, che possiamo chiamare polo (dall’altra parte della sfera determina un punto diametralmente opposto Q, detto antipodale). Consideriamo due piani qualsiasi che passino per il centro e che siano perpendicolari al piano, ossia che passino per l’asse QOP. La loro intersezione con la superficie sferica dà luogo ad altri due cerchi massimi, PCAQ e PDBQ (abbiamo tracciato solo la parte che sta “davanti” per evitare troppe linee, ossia abbiamo tracciato solo dei semicerchi massimi).
Tanto per gradire, possiamo anche dire che la parte di superficie sferica (azzurra) compresa tra questi due semicerchi massimi prende il nome di fuso sferico, ma a noi interessa relativamente…
Consideriamo, invece, solo la figura sferica PAB. Che cos’è? Beh… dovremmo ormai saperlo molto bene. Essa è composta da tre segmenti di cerchio massimo e quindi è un triangolo sferico a tutti gli effetti. Possiamo subito chiamare a, b, c i suoi lati, sapendo esattamente che coincidono, misurati in radianti, con gli angoli corrispondenti al centro della sfera.
Facendo questo gioco, scopriamo subito che il lato rettilineo (intrinseco) PA non è altro che:
PA = b = π/2
Così come
PB = c = π/2
La stessa cosa varrebbe per qualsiasi cerchio massimo passante per P (e Q). Ad esempio:
PM = PN = π/2
Infine si ha che:
AB = a
Non è difficile immaginare che a varia al variare dei due piani verticali e che quindi potrebbe benissimo essere uguale a π/2. In poche parole, il triangolo sferico PAB potrebbe tranquillamente avere i sui tre lati uguali a π/2.
Ancora più interessante è il calcolo degli angoli α, β e γ. Ormai sappiamo che si determinano guardando l’angolo tra le tangenti ai cerchi massimi nel punto di vertice. Ne segue che β e γ risultano essere proprio uguali a 90° (le tangenti sono perpendicolari per costruzione), mentre α dipende dall’angolo diedro formato dai due piani perpendicolari al piano orizzontale o, se preferite, dalle due tangenti rosse in P.
Prima di proseguire con il quiz, deduciamo subito una caratteristica veramente peculiare della geometria sferica (ma che già avevamo intuito). Le rette parallele si incontrano tutte in un punto.
Tutti i cerchi massimi perpendicolari al cerchio orizzontale sono paralleli tra loro (ognuno forma un angolo di 90° con lui). Sappiamo, però, che i cerchi massimi sono le rette intrinseche, così come lo è il cerchio orizzontale, per cui abbiamo un fascio di rette che formano lo stesso angolo con un’altra retta. Nella geometria euclidea ciò vuol dire che sono rette parallele. Tuttavia, nel caso sferico, tutte queste rette intrinseche parallele devono passare per il polo P, ma anche dal punto antipodale Q. Possiamo quindi dire che per due punti qualsiasi di una sfera passa un solo cerchio massimo, ma se i punti sono antipodali passano infinite rette parallele tra loro. Il che vuole anche dire che due rette qualsiasi (cerchi massimi) devono sempre avere due punti in comune (polo e punto antipodale).
Fatemi fare anche una riflessione, che sarà molto utile se un giorno decideremo di rappresentare i buchi neri nel diagramma di Penrose: “I poli di un cerchio massimo possono rappresentare i punti all’infinito di un fascio di rette parallele”.
Torniamo a noi e alla soluzione del quiz, che ormai dovreste intuire perfettamente. Partiamo da P e andiamo in linea retta verso A. Attenzione! Guai a cercare di abbreviare il percorso e piegare di 90° nel punto C. Ci troveremmo su un cerchio intrinseco (arco verde) che non è rettilineo e quindi non corrisponde ai requisiti del quiz. Dobbiamo proseguire fino ad A dove incontriamo il cerchio massimo “rettilineo” AB che si segue proprio dopo aver piegato di 90° (angolo γ). Continuiamo ad andare dritti fino al punto B e poi giriamo di 90° (angolo β) prendendo il cerchio massimo BP che ci riporta fino al punto di partenza.
Notiamo che possiamo scendere e risalire secondo qualsiasi cerchio massimo il cui piano sia perpendicolare a quello orizzontale. In altra parole, l’angolo α può essere qualsiasi. Magari proprio uguale a 90°. In questo caso otteniamo un triangolo sferico i cui tre lati sono uguali tra loro e a π/2 (ossia 90° espressi in radianti) e i cui tre angoli sono anch’essi uguali tra loro e a 90°. Mamma mia… che strano mondo sferilandia! Ci sarebbero da osservare molte cose, ma almeno una deve essere detta subito, attraverso una semplice somma:
α + β + γ = 90° + 90° + 90° = 270°
Accidenti… questa è proprio una scoperta eccezionale: la somma degli angoli di un triangolo sferico può superare abbondantemente i 180°. Non solo, però: la somma varia al variare del triangolo. Si dimostra subito, facendo variare l’angolo α: il triangolo sferico ABP mantiene due angoli uguali a 90°, mentre il terzo può cambiare sia in più che in meno…
Bene, prima di passare a operazioni più pratiche, una facile domanda: Fino a quale valore può arrivare la somma degli angoli di un triangolo sferico. Teniamo presente che se un angolo raggiunge 180° il vertice sparisce e cadremmo in un caso degenere (tre vertici su uno stesso cerchio massimo non possono esistere)
Tanto che ci siamo, eccovi anche un problemino un po’ più complicato…
QUIZ sui cerchi minori
Consideriamo la Fig. 13, dove abbiamo un cerchio massimo orizzontale su cui è evidenziato un arco AB.
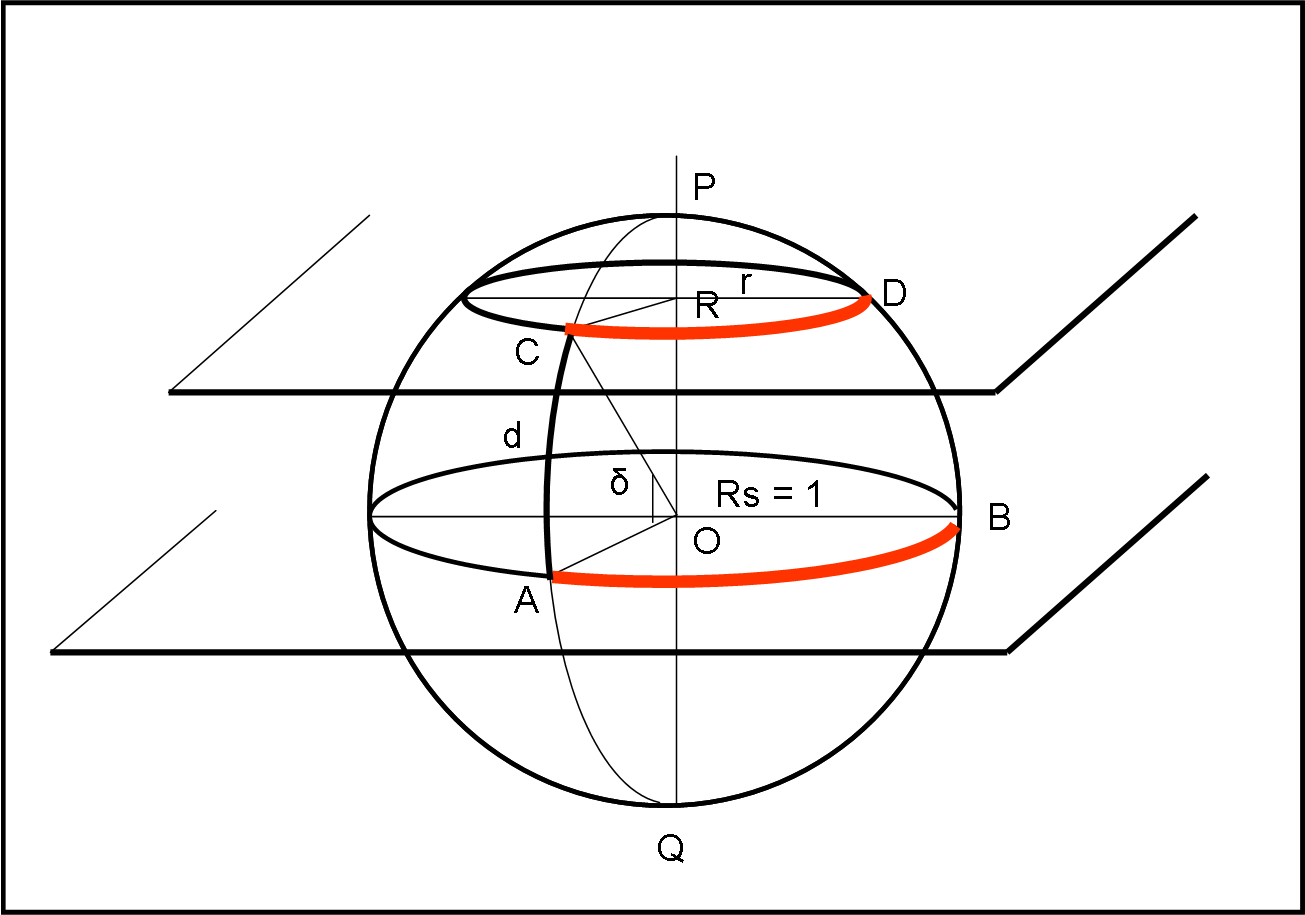
Tagliamo la sfera con un piano non passante per il centro ma parallelo a quello orizzontale. Otteniamo un cerchio minore di centro R e raggio r. Immaginiamo di conoscere l’arco di cerchio massimo AC = d, ossia l’angolo al centro COA= δ (sono la stessa cosa, a parte che l’arco si esprime in radianti). Conoscendo la misura di AC, quanto vale l’arco di cerchio minimo CD, in funzione di AB?
Nella prossima puntata cominceremo con la soluzione dei due quesiti e poi torneremo alla trigonometria piana per conoscerla un po’ meglio…






17 commenti
La prima domanda che hai posto, Enzo, me l'ero già posta leggendo l'articolo, ma mi manca un dato per rispondere... facendo, per esempio, riferimento alla fig. 12, questa individua un solo triangolo sferico (quello evidenziato in azzurro e caratterizzato dall'angolo in P), oppure individua anche il suo complementare che ha in P un angolo pari a
in P), oppure individua anche il suo complementare che ha in P un angolo pari a ) ?
?
No, no, ho fatto un pasticcio... volevo dire pigreco non 2pigreco. Per un angolo uguale a pigreco il vertice... sparisce... SCUSATE!!!!
Cancello i due commenti precedenti per non creare confusione e aggiungo una frase nel testo...
Quindi se
allora
O no?
Ma perché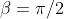 ,
, 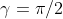 ????
????
Non vorrei che leggendo l'articolo qualcuno ritenesse OBBLIGATORIO il fatto che un lato di un triangolo debba stare sul cerchio massimo orizzontale. Io ho preso quello solo per risolvere il vecchio quiz... Ricordiamo che per due punti qualsiasi di una sfera passa sempre un cerchio massimo (uno solo, tranne che nel caso speciale di due punti antipodali dove ne passano infiniti). Magari aggiungo qualcosa nel testo...
...hai giá risposto da solo: avevo proprio capito così!
CD=AB*cosAC
Da quello che ho capito l'angolo al centro della sfera, in radianti, è la lunghezza dell'arco su un cerchio massimo se si considera la sfera di raggio unitario
AB è su un cerchio massimo e quindi la sua lunghezza è α (angoli in radianti e Rs=1)
questo cerchio massimo lo definisco equatoriale (devo pur dare dei nomi per spiegarmi)
i piani che sono perpendicolari al piano equatoriale e passano per il centro della sfera sono un fascio di piani definito dalla retta loro intersezione passante per il centro, la retta che definisce il fascio è perpendicolare al piano equatoriale
questa retta interseca la sfera in due punti opposti: i poli
l'angolo diedro tra due di questi piani contenenti i punti A e B è pari ad α
che è lo stesso angolo di apertura dell'arco CD perché i due punti giacciono sugli stessi piani che formano il diedro e l'arco è costruito su un piano parallelo al piano equatoriale, cioè perpendicolare ai piani suddetti
l'arco CD è un arco di circonferenza di raggio pari a Rs*cosδ =cosδ sotteso da un angolo α
l'angolo δ è costruito su uno dei piani passanti per il centro dunque lungo un cerchio massimo per cui AC=δ
allora la lunghezza CD=Rs*α*cosδ=α*cosδ=AB*cosδ=AB*cosAC
non dirò niente fino alla soluzione che sarà nel prossimo articolo "curvo" 8-)
Beh... nessuno ha voglia di "curvarsi"? Forza, almeno la prima risposta... E poi solo Gianni per la seconda?
Il valore massimo della somma degli angoli di un triangolo sferico arriva a sfiorare 360°
90+90+la massima apertura consentita al diedro fra i due piani che costruiscono i lati meridiani del triangolo sferico sulla sfera <180
escludendo 180 perché i due meridiani sarebbero lo stesso meridiano
escludendo >180 perché il triangolo (convesso?) si sposta solo dall'altra parte
caro Gianni: ricordiamoci la definizione di triangolo sferico. Deve essere formato da tre archi di cerchio massimo...
credevo di avere proprio considerato quanto mi dici:
un arco di cerchio massimo (meridiano A) ottenuto dall'intersezione del piano passante per il polo ed il centro
un secondo arco di cerchio massimo (B) uguale al primo ma facente un diedro alfa
un terzo arco di cerchio massimo è quello prodotto dal piano passante per il centro e perpendicolare ai precedenti (equatoriale)
gli angoli tra meridiani ed equatore sono di 90 gradi quindi 90+90
resta l'angolo alfa che è variabile a seconda dell'apertura che si da al diedro, tale apertura può raggiungere 180 (un soffio di meno)
a 180 non ci sono due piani meridiani ma uno solo
... o forse dovevo parlare semipiani, se parlo di piani devo considerare che vengono generati quattro diedri, due acuti e due ottusi per cui il triangolo massimo ha un diedro alfa di 90 gradi per cui la somma è 270 al massimo.
considerato un triangolo sferico così come definito da Enzo, e visibile nella figura allegata, ciascuno dei suoi angoli interni, divaricando le circonferenze massime su cui giacciono i suoi lati, può arrivare a poco meno di 180 gradi. Quindi la somma dei tre angoli interni di un triangolo sferico ha il valore limite di 180 x 3 = 540 gradi. Valore limite che però non può essere raggiunto, altrimenti il triangolo degenera in una circonferenza massima.
o, meglio, altrimenti il triangolo diventa una semisfera...
caro Gianni M.,
Tu dici: "Un terzo arco di cerchio massimo è quello prodotto dal piano passante per il centro e perpendicolare ai precedenti (equatoriale)". ma perché lo vuoi prendere perpendicolare?
credevo perché un terzo arco di un cerchio massimo avrebbe prodotto angoli di 90 gradi pensando fosse il massimo possibile
invece credo possano raggiungere quasi 180 e quindi tre angoli di quasi 180 gradi fa quasi 540 !!!
come dice Arturo
Caro Enzo, si provo anch'io.
Alla seconda domanda risponderei con una figura....
Non penso sia necessario aggiungere altro...
Sulla prima domanda devo ammettere che io avrei risposto come ha fatto inizialmente Gianni.
devo ammettere che io avrei risposto come ha fatto inizialmente Gianni.
Poi sia la tua obiezione, sia Arturo mi avete convinto che la somma massima è di poco inferiore a 540° (180° x 3)... di poco inferiore poiché i singoli angoli possono avvicinarsi a 180°, senza pero giungere a tale apertura...
Per me però non è facile immaginare un simile triangolo... o un triangolo che gli si avvicini...
Ci ho provato con questa figura partendo dal presupposto che ogni tratto di cerchio massimo è un segmento (tratto di retta), per cui in questo modo ho disegnato i 3 lati del triangolo..
Non so però se è corretta una simile rappresentazione (gli angoli non sono di 180°, ma sono piuttosto aperti)...
Paolo