Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Vorremmo continuare con la descrizione della trigonometria sferica per potere poi maneggiare senza problemi la sfera celeste e le posizioni dei corpi che sono proiettati su di lei. Tuttavia, è prima necessario introdurre dei teoremi di trigonometria piana che avevamo tralasciato descrivendone le basi. Prima ancora, però, diamo le soluzioni ai due quiz proposti la volta scorsa.

La prima è veramente semplice: basta pensare che se uno dei tre angoli raggiungesse 180°, automaticamente i tre vertici apparterrebbero alla stessa circonferenza e cadrebbe la definizione di triangolo. Ne segue che il valore limite, per la degenerazione del triangolo, è dato da 3∙180° = 540°. Un triangolo sferico vicino al limite massimo della somma dei tre angoli è riportato nella Fig. 14.

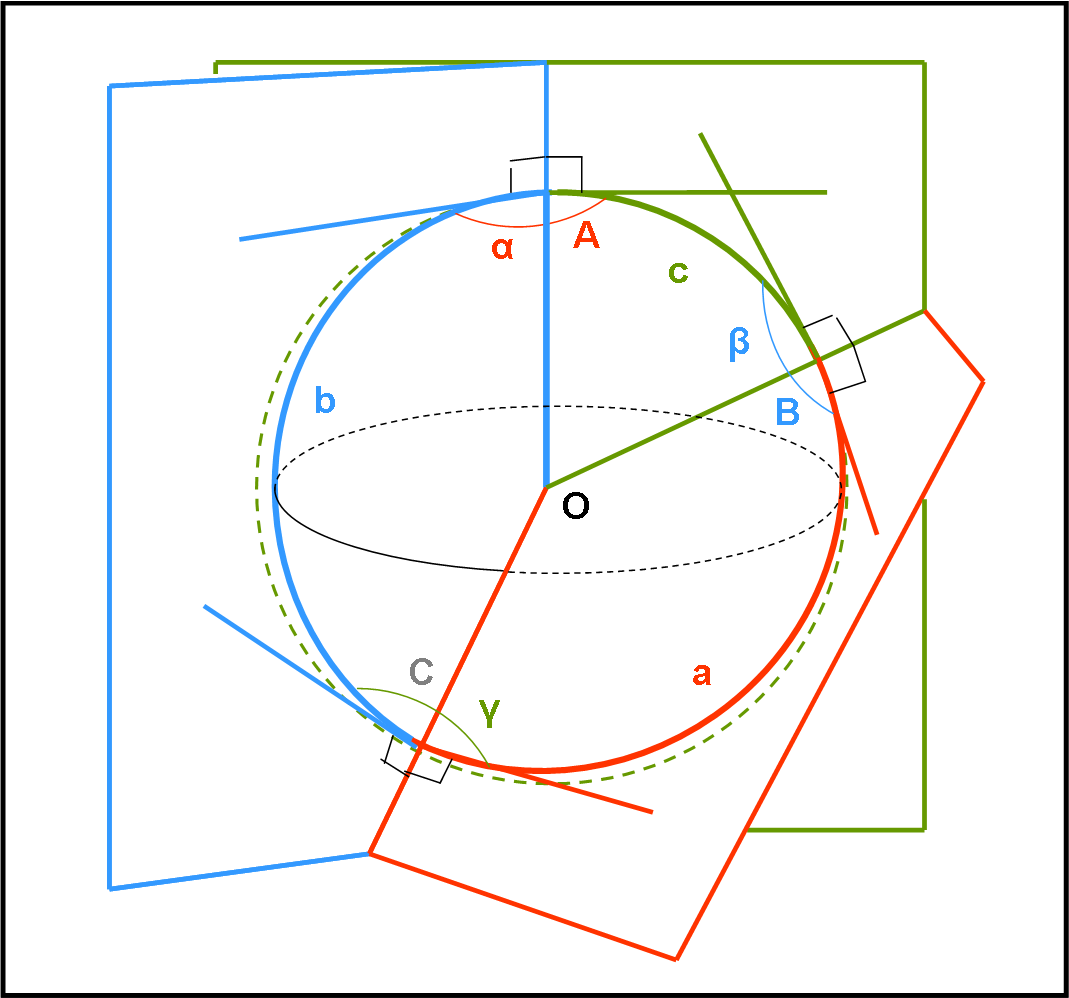
I tre lati sono relativi ai tre piani di colore diverso (rosso, blu e verde). Il cerchio verde è quello che giace sul piano del foglio. Poco importa se i lati curvano e se gli angoli si allargano, l’importante è che si utilizzino tre piani passanti per il centro della sfera.

Più interessante e utile è la soluzione del secondo quiz. Dato un cerchio massimo cerchiamo di stabilire la relazione che vi è fra un suo arco, compreso tra due cerchi massimi a lui perpendicolari, e i cerchi minori ottenuti, compresi sempre tra i due cerchi massimi, a differente distanza da lui. Il tutto è rappresentato molto meglio nella Fig, 15 che non è altro che la Fig. 13, presentata nel QUIZ .

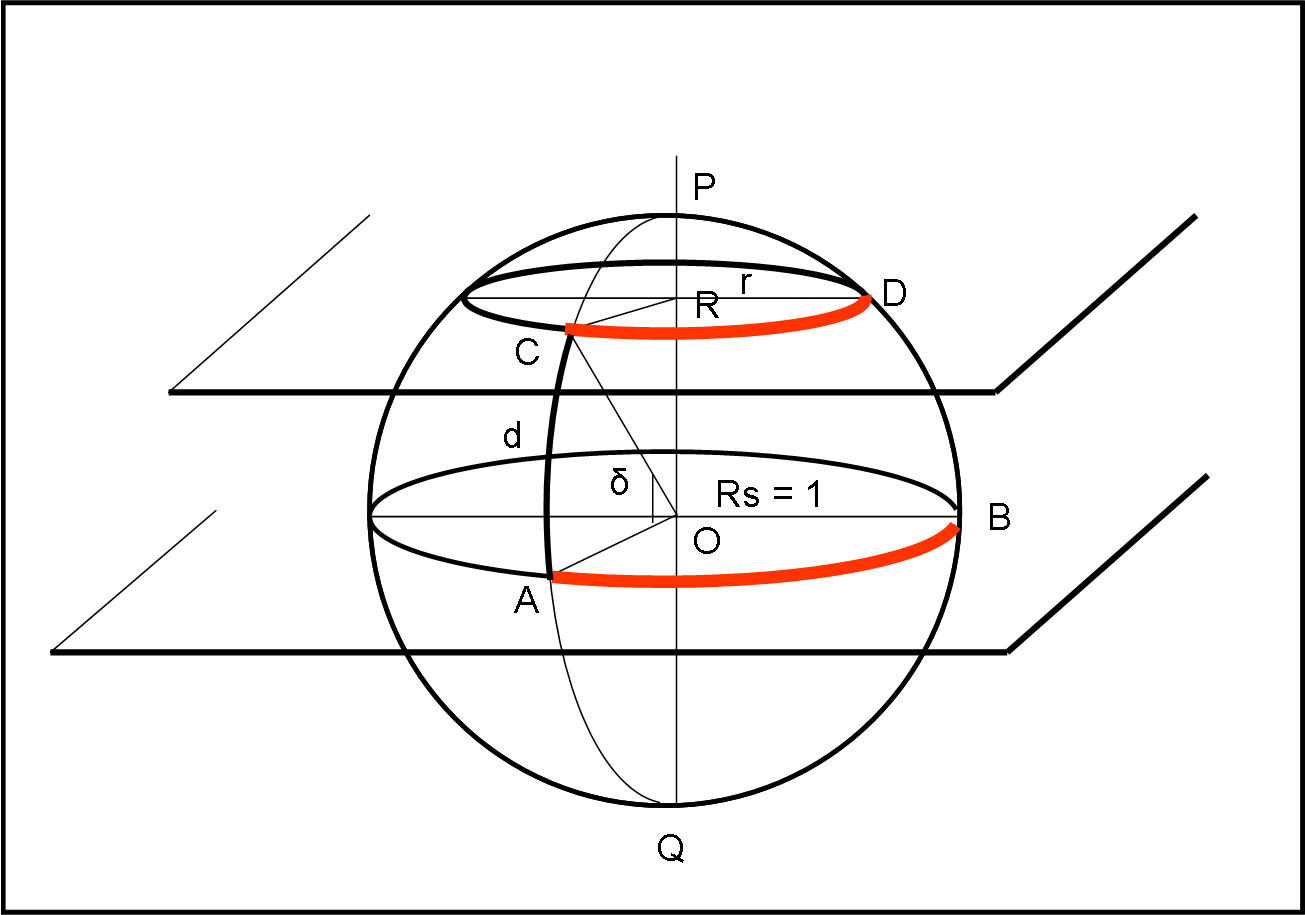
Conosciamo AB e vogliamo trovare CD per varie posizioni lungo la sfera celeste. Si capisce subito l’importanza di questa relazione pensando alle misure lungo i paralleli terrestri…

Chiamiamo δ l’angolo al centro che determina la posizione del piano non passante per il centro. Per δ = 0 il cerchio minore coincide con il cerchio massimo, per δ = 90°, il cerchio degenera nel punto P. Cosa analoga (cambiando di segno) capita nell’emisfero in basso.

La definizione dell’angolo δ identifica immediatamente l’arco di cerchio AC, dato che essi sono esattamente uguali assumendo Rs = 1. Chiamiamo d questo arco, ricordando bene che:

d = δ (rad.)

Consideriamo il triangolo rettangolo CRO. CR non è altri che il raggio r (estrinseco) del cerchio minore. L’angolo COR vale, ovviamente, 90° – δ = π/2 – d. CO è il raggio della sfera e vale 1.

Ne segue che:

r = Rs sen (π/2 – d) = cos (d)

L’arco di cerchio CD vale, però:

CD = r ∙ angolo (CRD)

L’arco di cerchio AB vale anche:

AB = Rs ∙ angolo (AOB) = angolo (AOB)

Ma l’angolo AOB è uguale all’angolo CRD, dato che entrambi sono formati dagli stessi due piani e sono misurati su piani a loro perpendicolari o (se preferite) sono formati da coppie di rette parallele.

Ne segue che:

CD = r ∙ angolo (CRD)  = r ∙ angolo (AOB) = r ∙ AB

Ma abbiamo appena trovato che:

r = cos (d)

Si ha infine:

CD = AB cos (d)

In poche parole l’arco di cerchio minore è uguale all’arco di cerchio maggiore corrispondente (relativi a due piani paralleli), moltiplicato per il coseno dell’arco di cerchio massimo che li separa.

Questa è una formula estremamente importante per le coordinate sferiche.

Facciamo adesso un passo indietro e torniamo alla trigonometria piana. L’abbiamo trattata parzialmente QUI, ma è adesso necessario aggiungere qualche nozione e almeno un paio di formule. Alcune le avevamo già ricavate e/o usate affrontando il QUIZ su stellarium (QUI, QUI e QUI).

Teorema dei seni

Consideriamo un triangolo (piano) ABC qualsiasi, come mostrato in Fig. 16

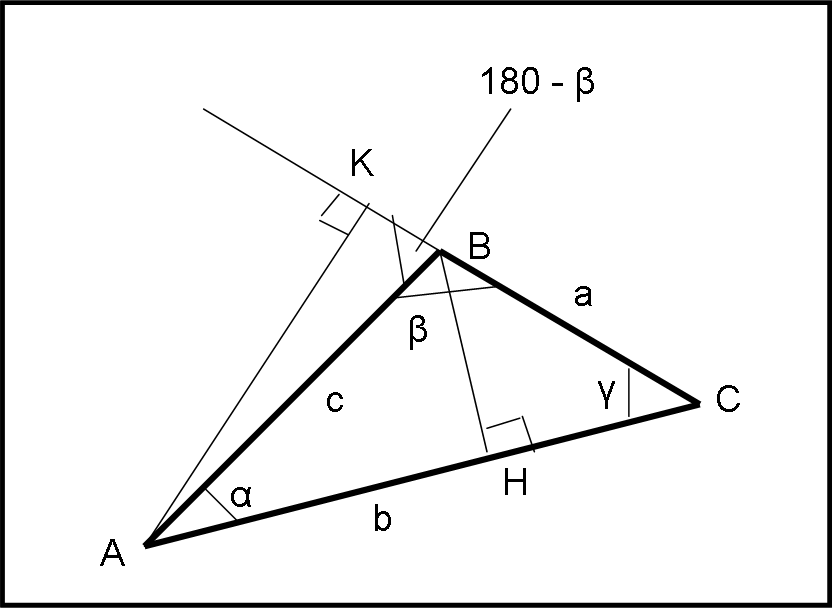
Tracciamo da B la perpendicolare al lato opposto e sia H il punto di intersezione. Otteniamo due triangoli rettangoli, AHB e CHB.

Dal primo abbiamo:

BH = c sen (α)

Dal secondo:

BH = a sen (γ)

Uguagliando:

c sen (α) = a sen (γ)

O, ancora:

c/sen (γ) = a/sen (α)       …. (2)

Tradotto in  parole: il rapporto tra un lato e il seno dell’angolo opposto rimane costante.

Proviamo con un altro vertice:

Tracciamo da A la perpendicolare al lato BC e chiamiamo K il punto d’intersezione (prolungando il lato, ovviamente).

I due triangoli AKB e AKC sono rettangoli. Possiamo quindi scrivere:

AK = c sen (180 – β) = c sen (β)

AK = b sen (γ)

Uguagliando:

c sen (β) = b sen (γ)

E, ancora:

c/sen (γ) = b/sen (β)

Ricordando la (2)

Si ha la formula generale dei seni:

c/sen (γ) = a/sen (α) = b/sen (β)      …. (3)

Il teorema di Carnot

Questo teorema, detto anche del coseno, permette di ricavare un lato di un triangolo qualsiasi, conoscendo gli altri due e l’angolo tra essi compreso. Utilizziamo la Fig. 17.

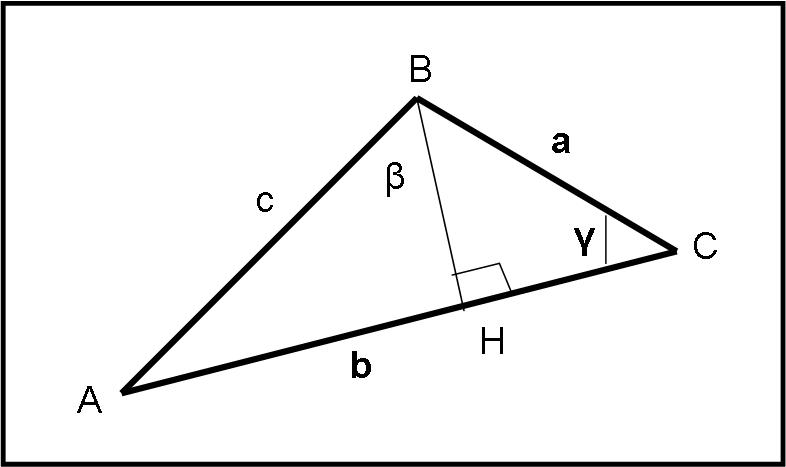
Conosciamo a, b e l’angolo γ e vogliamo ricavare il lato c.

Tracciamo da B la perpendicolare BH al lato b = AC.

Dal triangolo rettangolo BHA si ha:

c² = AH² + BH²         …. (4)

dal triangolo rettangolo BHC, si ha:

BH = a sen (γ)

Ma vale anche:

AH = b – HC = b – a cos (γ)

Sostituendo le ultime due relazioni nella (4) si ha:

c² = AH² + BH² = (b – a cos (γ))² + a² sen²(γ) = b² + a² cos²(γ) – 2ab cos (γ) + a² sen²(γ)

 

Abbiamo, raccogliendo a²:

c² = b² + a² (cos²(γ) + sen²(γ)) – 2ab cos (γ)

Ricordando che

sen²(γ) + cos²(γ) = 1

si ha, infine:

c² = a² + b² - 2ab cos (γ)       …. (5)

La (5) rappresenta la formula di Carnot

Essa si riduce al teorema di Pitagora quando l’angolo  γ vale 90°, dato che il coseno va a 0. La formula, ovviamente può applicarsi a qualsiasi lato, facendo “girare” le lettere.

Secante, cosecante e cotangente

Da un punto di vista puramente matematico è immediato definire la secante (sec), la cosecante (cosec) e la cotangente (cotan):

sec (ϑ) = 1/cos (ϑ)

cosec (ϑ) = 1/sen (ϑ)

cotan (ϑ) = 1/tan (ϑ)

Da un punto di vista grafico, basta richiamare il cerchio goniometrico di raggio unitario, come si vede in Fig. 18

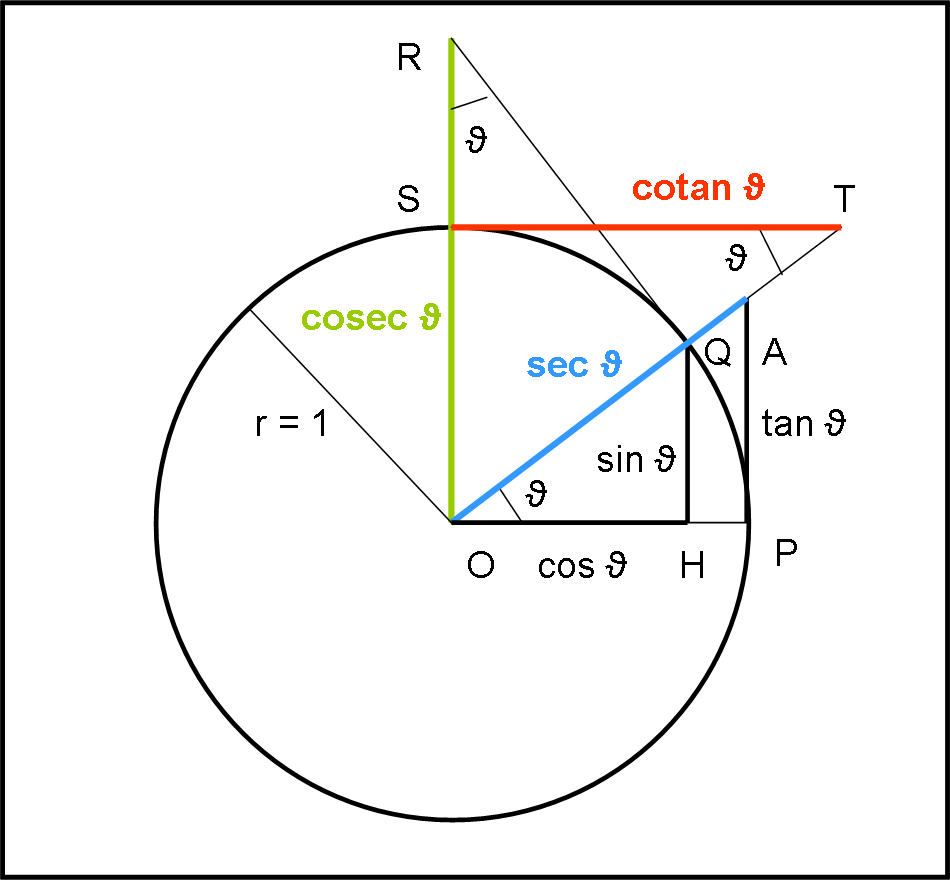
I triangoli rettangoli OHQ e OPA sono simili e quindi vale la proporzione:

OH : OP = OQ : OA

OA e la secante di ϑ

Infatti:

sec (ϑ) = OA = OP ∙ OQ/OH = 1∙1/cos (ϑ) = 1/cos (ϑ)

Nel triangolo rettangolo OPA, il teorema di Pitagora ci dice anche che:

sec²(ϑ)  = OP² + PA² = 1 + tan²(ϑ)       …. (6)

Ricaviamo geometricamente anche la cosec (ϑ), tracciando la tangente alla circonferenza goniometrica nel punto Q e considerando il triangolo rettangolo OQR. Quest’ultimo è simile al triangolo OQH (due angoli uguali). Ne segue che OR = cosec (ϑ). Infatti:

OR : OQ = OQ : QH

Ossia:

cosec (ϑ) = OR = OQ ∙ OQ/QH = 1/sen (ϑ)

Possiamo anche definire la funzione

cotan (ϑ) = 1/tan (ϑ) = cos (ϑ)/sen (ϑ)

Geometricamente essa è rappresentata dal segmento ST. Infatti, dai triangoli simili OST e OHQ si ha:

ST : SO = OH : QH

e, quindi:

cotan (ϑ) = ST = SO ∙ OH/QH = 1∙ cos (ϑ)/sen (ϑ) = cos (ϑ)/sen (ϑ)

Non preoccupatevi… useremo soltanto la definizione di secante, ma è più che giusto conoscere queste funzioni così semplici, sia matematicamente che geometricamente. Chi vuole divertirsi (ma non è importante per il proseguo della trattazione) può anche fare il grafico delle tre funzioni sec, cosec e cotan. Un bell’esercizio per ricordare lo studio di funzioni…