Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nel nostro percorso, abbiamo trovato due insiemi particolari, che non sono numerabili; l'insieme delle parti di N, e l'insieme R dei reali. Indicheremo nel seguito con  la cardinalità delle parti di N, e con c la cardinalità di R. Che relazione c'è fra , e c ? Vedremo che sono uguali. Non possiamo però arrivarci subito, ma dobbiamo farlo per gradi, sfruttando il teorema di Bernstein.

In questo articolo vogliamo dimostrare  che la cardinalità dell'insieme delle parti è minore o uguale a c , ovvero <=c

Per far ciò useremo un insieme, detto insieme di Cantor, definito tramite un metodo iterativo. Ancora una volta la ricorsione gioca un ruolo essenziale nell'ambito degli insiemi infiniti .

Prima due concetti importanti .

Successioni binarie e insieme delle parti.

Nell'articolo  sull'insieme delle parti abbiamo dimostrato che il numero di sottoinsiemi di un certo insieme X contenente n elementi è . Per farlo abbiamo usato una corrispondenza fra i sottoinsiemi di X e le sequenze di 0,1

Ricordiamo che possiamo elencare i sottoinsiemi di X in questo modo (caso in cui n=3,X={a,b,c}), usando una combinazione di tre elementi xyz dove x,y,z valgono 0 o 1; facciamo corrispondere al sottoinsieme una sequenza di 0,1 che ci dice se l'elemento è presente o no. Ad esempio

101

1	0	1
a	b	c

corrisponde  al sottoinsieme {a,c}. Così otteniamo tutti i sottoinsiemi di X.In pratica abbiamo creato una corrispondenza biunivoca fra le sequenze di 0,1 di lunghezza 3 e i sottoinsiemi di X. Vogliamo adesso estendere questo fatto al caso in cui X sia infinito, in particolare X=N; in tal modo definiamo proprio delle successioni. Estendiamo dunque al caso infinito; consideriamo delle sequenze 010101111.... infinite di 0,1; esse sono in corrispondenza biunivoca con i sottoinsiemi di N, quindi con l'insieme delle parti di N.  Quindi tali successioni, non sono un un insieme numerabile, ma hanno la stessa cardinalità di P(N).

Vediamolo più in dettaglio nel caso di N ; indico con  h: ---> P(N)   l'insieme di tutte le successioni binarie infinite,

0	1	2	3	4	5	..	n	..	..
a1	a2	a3	a4	a5	a6	..	an	..	..

Gli ai possono valere o zero o uno a seconda che l'elemento ci sia o no e definisce un sottoinsieme di N;

l'applicazione h: ---> P(N) sopra descritta è biunivoca; infatti successioni che differiscono per almeno un elemento generano sottoinsiemi diversi  di N; h è anche suriettiva, perchè dato un qualsiasi sottoinsieme di N,ad esempio A={4,6,8,...},possiamo costruire la successione che ha per immagine A;   partiamo dalla prima cifra della successione che sarà 0 perchè zero non compare, e così pure la seconda perchè 1 non compare e così via, otteniamo la successione 0000101010000...

0	1	2	3	4	5	6	7	8	..
0	0	0	0	1	0	1	0	1	..

L'Albero binario completo

Cominciamo dalla definizione di albero che è intuitiva; non è altro che un albero vero e proprio, come quelli che esistono in natura. Oppure si può pensare ad un albero genealogico, in cui la radice è il capostipite. Per ramo intendiamo una successione  di elementi, ognuno figlio del precedente, che parte dal capostipite. Un nodo corrisponde alle biforcazioni di due rami.

 

 

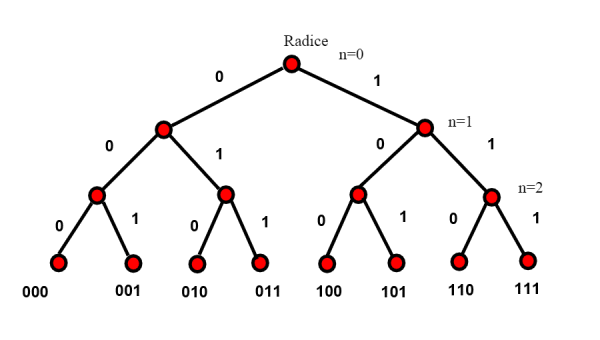
Un tipo particolare di albero è l'albero binario. Un albero binario è caratterizzato dal fatto che ogni nodo può avere al massimo due figli. Un albero binario è completo quando i figli sono esattamente sempre due.

Quante sono  i rami terminali un albero binario completo? Dipende dalla profondità dell'albero, che chiamiamo n. Partendo dalla radice, n=0 , e procedendo ad ogni diramazione (nodo) abbiamo due  nuovi rami , quindi 2*2...*2 n volte, ovvero . Vediamo questo fatto in altro modo; Per ogni livello n possiamo pensare di percorrere l'albero andando a destra o sinistra in ogni nodo. I possibili percorsi (rami) sono tanti quante le sequenze di 0,1 (poniamo 0 se andiamo a sinistra, 1 se andiamo a destra. Nel caso n=3 abbiamo le sequenze del disegno che identificano tutti i rami, sono sempre 

Concentriamoci adesso su un albero binario infinito; quanti sono i rami (nel senso di cardinalità)? Come nell'esempio finito, partendo dalla radice, ogni volta ho due possibilità di scelta (andare a destra o a sinistra. Ho delle sequenze di 0,1 ovvero delle sequenze binarie  infinite visto che la profondità dell'albero è infinita. Ma abbiamo visto che le successioni binarie sono tante quante l'insieme delle parti di N, P(N). Quindi la cardinalità di un albero binario completo infinito è 

L'insieme di Cantor, un albero binario completo

Consideriamo un segmento chiuso AB=[0,1]; sappiamo che AB è equipotente a tutto R. Dividiamo il segmento AB in tre parti uguali

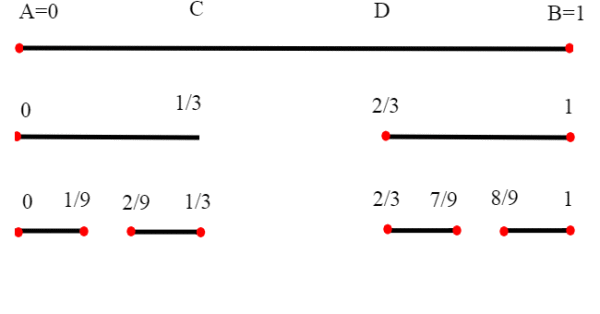
e togliamo dalla parte centrale il segmento aperto (C,D) otteniamo due segmenti chiusi, di lunghezza 1/3 di AB. Se ripetiamo il procedimento ai due segmenti rimasti, dividendoli sempre in tre parti otteniamo in tutto quattro segmenti, di lunghezza 1/9 di AB. Vogliamo estendere questo procedimento indefinitamente; cosa resta del segmento AB=[0,1] iniziale, dopo tutte le cancellazioni? L'insieme di Cantor. Osserviamo che non resta alcun segmento non degenere, infatti la lunghezza all'n-esima iterazione è , che ha come estremo inferiore 0 ,o <(se preferite) limite zero.

Restano allora solo dei punti (da qui il termine suggestivo "polvere di Cantor"). L'insieme senz'altro non è vuoto(gli estremi di un segmento non vengono mai cancellati,viene solo tolta la parte centrale).Quanti sono questi punti?

Osserviamo che l'insieme di Cantor è un albero binario completo.

 

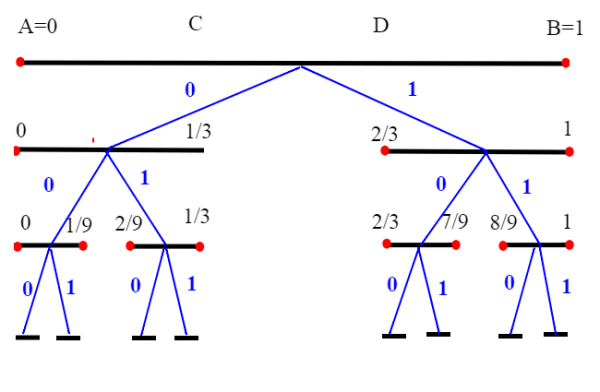
Ogni volta che dividiamo i segmenti successivi in tre parti e togliamo il segmento (aperto) centrale, abbiamo due scelte; prendere quello di sinistra, oppure quello di destra. Gli intervalli che corrispondono ad un certo ramo sono tutti incapsulati; ovvero ogni precedente contiene i successivo;sono intervalli chiusi e la loro ampiezza tende a zero (è uguale a); per quanto abbiamo visto su gli intervalli incapsulati, la loro intersezione è un unico punto). Quindi per ogni ramo  abbiamo nell'insieme di Cantor almeno un punto.

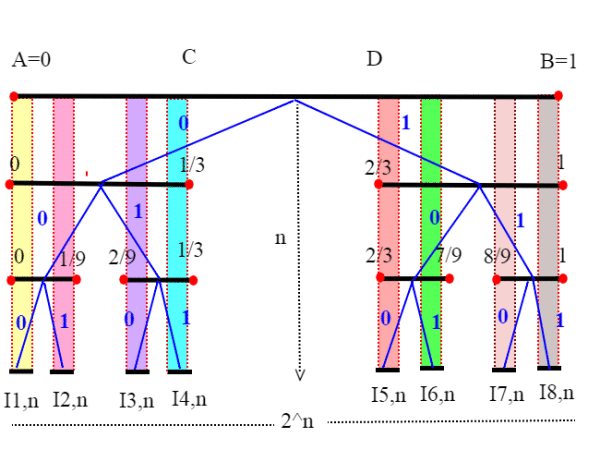
Ma i rami  dell'insieme di Cantor sono almeno tanti quanti le successioni binarie infinite, ovvero ;  vogliamo cioè dimostrare che <=|C| .Per far questo basta provare che la funzione h:-->|C| che a una successione binaria associa quel punto che è l'intersezione dei relativi intervalli incapsulati, è iniettiva. Se a,b sono due successioni di , e , allora esiste almeno un n tale che . per comodità prendiamo il più piccolo n per cui questo si verifica. Sappiamo che gli an, ovvero le successioni di 0,1 che determinano un ramo, individuano gli intervalli incapsulati; ma se in n , vuol dire che ho scelto di andare in una successione a sinistra e nell'altra a destra (fino a n-1 gli intervalli erano gli stessi); quindi vado a finire in due intervalli disgiunti, e l'intersezione finale di tutti gli intervalli non può essere la stessa.

Se indichiamo con |C| la cardinalità dell'insieme di Cantor, |<=|C|<=|[0,1]|=c

Infatti <=|C| perchè come abbiamo visto la funzione h è iniettiva; del resto C è contenuto in [0,1], quindi C|<=|[0,1]; sappiamo poi che la cardinalità di [0,1] è uguale a quella di c.

Il nostro scopo è stato raggiunto; la prossima volta dimostreremo la disuguaglianza opposta  (c<=)

e potremmo concludere ( grazie al teorema di Bernstein) che =c; per finire volevo illustrare delle proprietà di un insieme che si è dimostrato molto fertile.

 

Definizione formale

Per definire l'insieme di Cantor formalmente, chiamiamo Co=[0,1], C1 quello che resta dopo la prima cancellazione, C1=[0,1/3]  U [2/3,1]

C2 = [0, 1/9] [ [2/9, 1/3] [ [2/3, 7/9] [ [8/9, 1]  quello che resta dopo la seconda cancellazione, ecc.

Allora insieme di Cantor: 

Non ho dato subito questa definizione , perchè poteva generare confusione. Ora che abbiamo visto come si estendono le successioni di intervalli su rami disgiunti, osserviamo che i C0,C1,..Cn sono tutti inclusi nel precedente,quindi la loro intersezione al passo iterativo n, non è altro che Cn, ovvero quello rimane all'n-esima cancellazione. Quindi quando il processo iterativo diventa infinito, Cn diventa proprio l'insieme di Cantor.

L'insieme di Cantor ha misura nulla.

Possiamo definire la misura di un intervallo, semplicemente facendo la differenza fra gli estremi.

Vogliamo vedere qual'è la misura totale delle cancellazioni che vengono eseguite partendo dall'intervallo [0.1]. Alla prima iterazione tolgo un segmento di lunghezza 1/3 ; alla seconda due segmenti di lunghezza 1/9, ovvero 2/9, alla terza 4 segmenti di lunghezza 1/27, ovvero 4/27 e così via. La somma S delle misure che tolgo è quindi S=1/3 + 2/9 +  4/27 + .....

Quindi S è somma della serie :

abbiamo dunque un serie geometrica di ragione 2/3; sappiamo che la somma di tale serie è ,

S=3 *1/3

Quindi S=1.

Ma come definire la misura di un insieme di punti, come quello di Cantor? in questo caso possiamo farlo come differenza fra la misura di tutto l'intervallo e S.

Ma allora la misura dell'insieme di Cantor è l([0,1])-S=1-1=0

Questa è una cosa assai sconcertante, vi anticipo perchè. Abbiamo dimostrato che |<=|C|<=|[0,1]=c

Ma nel prossimo articolo, dimostreremo anche che |>=c, quindi che =c; ma allora riprendendo la diseguaglianza sopra c=|<=|C|<=|[0,1]=c, quindi |C|=c; L'insieme di Cantor ha addirittura la cardinalità della  retta R, ma la sua misura è nulla (mentre la retta ha misura infinita!)

L'insieme di Cantor è un frattale

Se chiamiamo C1,C2,C3,C4,.. i livelli della costruzione dell'insieme di Cantor, notiamo che i due blocchi in cui è diviso per ogni livello Cn+1 sono copie esatte ridotte di 1/3 di Cn.

Questo fatto non deve sorprenderci; Si può dimostrare che per come è definito, l'insieme di Cantor contiene infinite copie di se stesso, su scala diversa; questo è intuitivo, se cominciamo la costruzione da un qualsiasi pezzo dei  Cn dove eravamo arrivati e prima lo riscaliamo,  otteniamo ancora l'insieme di Cantor.

Esistono altre strutture geometriche, e non solo , ma anche in natura , che hanno questa proprietà (quella di contenere copie di se stesse ridotte di scala); basti pensare a un cavolfiore o  alle coste frastagliate. Se ingrandiamo le parti di questi oggetti, troviamo sempre che la parte ha una somiglianza con il tutto. Si dice che sono auto simili.

Fu  Mandelbrot, l'inventore del termine frattale; riportiamo di seguito le sue parole originali:
<<Ho coniato la parola frattale dall'aggettivo latino "fractus" Il corrispondente verbo latino "frangere"  che significa rompere  per creare frammenti irregolari. e pertanto sensibile  e quanto appropriato per le nostre necessità che, oltre a "frammentato" (come in frazione o in rifrazione), "fractus" dovrebbe anche significare "irregolare", con entrambi i significati preservati in  frammento".

(The Fractal Geometry of Nature,)>>

Può aprirsi davanti a noi un altro magico mondo, quello dei frattali ,visualizzati tramite iterazioni al computer in colori che dipendono da certi parametri delle iterazioni, che ci portano ad immagini fantastiche come questa (insieme di  Mandelbrot):

Pensate che il procedimento iterativo che conduce alla definizione è molto semplice; considero tutti i punti del piano complesso C; per ciascun punto definisco un successione ricorsiva in questo modo:

se tale successione è convergente, allora il punto appartiene all'insieme di Mandelbrot, altrimenti no. Si può dare colore nero se appartiene all'insieme, ma se poi si danno colori diversi a seconda della velocità di convergenza, allora si ottengono figure colorate come quella qui sopra. Naturalmente i frattali (o più precisamente le loro immagini) sono diventati di dominio pubblico dopo l'avvento del computer; prima esistevano solo nella mente dei matematici. Sembra che il primo frattale sia dovuto a Arthur Cayley, nel 1870, più un secolo prima della nascita della grafica al computer.