Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Definito il triangolo sferico, sia intrinsecamente che estrinsecamente, non ci resta che determinare alcune formule fondamentali che leghino tra loro  i lati e gli angoli. Esse vengono proprio chiamate le tre formule fondamentali della trigonometria sferica. Non è solo un gioco matematico, ma è la base per definire i sistemi di coordinate astronomiche e per passare da uno all’altro. Chi ha un telescopio sa benissimo che esso può essere sia altoazimutale che equatoriale. Bene, noi vogliamo svelare tutti i segreti delle varie montature, evidenziare i loro pregi e i loro difetti. Un qualcosa, quindi, che dovrebbe essere l’ABC degli astrofili anche più tecnologici e assidui adoratori di stellarium & co. Per tutti gli altri, una trattazione elegante ed essenziale per saper affrontare e descrivere ciò che avviene su una superficie sferica. La matematica la fa da padrona, ma non dimentichiamo la sua applicazione alla fisica più moderna, tipo la RG.

Introduciamo e spieghiamo molto attentamente la Fig. 19.

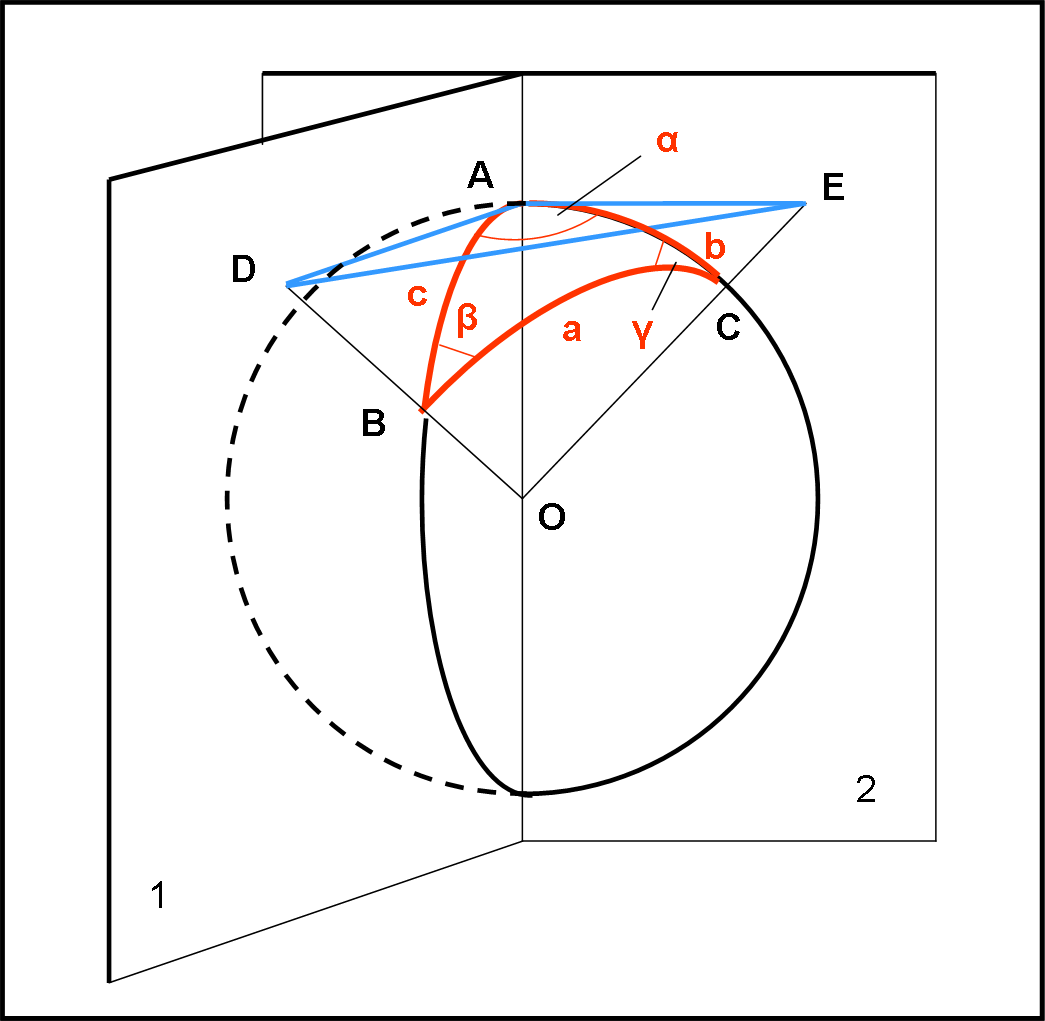
In essa è stato disegnato in rosso un triangolo sferico. Come tale esso deve avere per lati tre archi di cerchio massimo, che abbiamo chiamato a, b e c. Sappiamo benissimo che il raggio della sfera è unitario e quindi la misura dei tre lati non è altro che l’angolo che sottendono al centro della circonferenza, espresso in radianti. Non spaventiamoci dei radianti: è solo un modo diverso di rappresentare un angolo o un arco (che in questo caso coincidono). Esiste, perciò sia il seno di 90° sia il seno di π/2. Niente di strano, quindi, che d’ora in poi avremo a che fare con funzioni trigonometriche dei tre lati a, b e c. Essi sono angoli a tutti gli effetti e come tali li trattiamo.

Nella figura si sono evidenziati anche i due piani che individuano l’angolo sferico in A: li abbiamo chiamati 1 e 2. Essi contengono quindi i lati b e c e anche le rette tangenti ai cerchi massimi che i due piani determinano sulla sfera. Le rette tangenti sono AE e AD. L’angolo tra loro formato è proprio l’angolo α che viene considerato come l’angolo tra i lati b e c. Ne segue che il segmento OBD sta sul piano 1 e il segmento OCE sta sul piano 2. Dato che AE e AD sono tangenti ai relativi cerchi massimi in A, gli angoli DAO e EAO sono retti. Per chiarire ancora meglio la figura, ricordiamo che l’angolo α è l’angolo diedro formato dai piani 1 e 2. Inoltre, risulta ovvio (contiene due rette entrambi perpendicolari nello stesso punto all’asse OA) che il triangolo ADE giace su un piano perpendicolare all’asse OA.

Bene, dopo aver compreso perfettamente la figura, è ora di applicare ad alcuni suoi triangoli le funzioni trigonometriche, che conoscevamo già e che abbiamo imparato a conoscere la volta scorsa (in particolare la secante).

Iniziamo con il triangolo rettangolo OAD. Ricordiamo ancora una volta che l’angolo in O non è altro che l’arco c. Per facilitare la trattazione, riportiamo il piano del triangolo OAD sul piano del foglio nella Fig. 20.

 

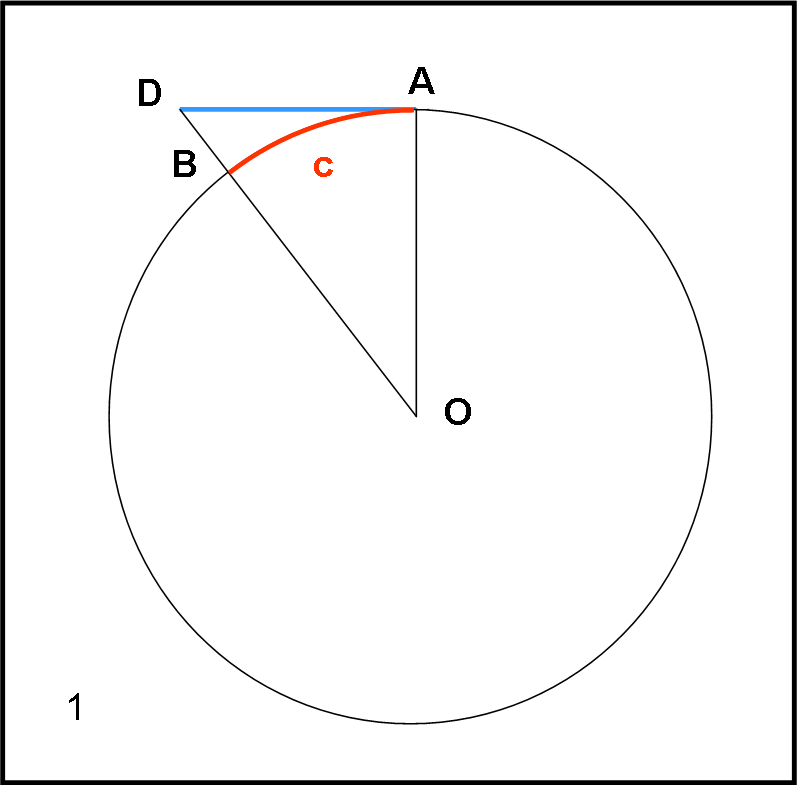
A questo punto, andando a rivedere quanto detto sulle secanti nel capitolo precedente (5), e ricordando, in generale, che la tangente è il rapporto tra il seno e il coseno, possiamo scrivere alcune relazioni e applicare qualche teorema.

Essendo OA = 1, si ha:

AD = tan (c)

OD = sec (c)

Analogamente dal triangolo piano AEO si ottiene:

AE = tan (b)

OE = sec (b)

Portiamoci adesso sul triangolo piano ADE. Esso è un triangolo qualsiasi di cui, però, conosciamo un angolo (DAE = α) e due lati (AD e AE). Per trovare il terzo lato, ossia DE, non ci resta che applicare il teorema di Carnot , descritto la volta scorsa.

DE² = AD² + AE² – 2AD∙AE cos (DAE)

Sostituendo quanto trovato, abbiamo:

DE² = tan²(c) + tan²(b) – 2 tan(c) tan(b) cos(α)      …. (7)

Consideriamo adesso il triangolo piano EDO (esso sta sul piano che definisce l’arco di cerchio massimo a).

Di lui conosciamo due lati (OD e OE) e l’angolo in O che è proprio uguale all’arco a. Mi raccomando! Non confondiamo l’angolo che uguaglia l’arco a con l’angolo α, che è tutt’altra cosa, come abbiamo appena visto.

Possiamo trovare nuovamente il lato DE attraverso questo triangolo, applicando anche a lui il teorema di Carnot:

DE² = OD² + OE² – 2 OD∙OE cos(DOE)

Sostituendo ciò che abbiamo ricavato precedentemente e ricordando che DOE = a, si ha:

DE² = sec²(c) + sec²(b) – 2 sec (c) sec (b) cos (a)        …. (8)

Uguagliano la (7) e la (8), otteniamo:

tan²(c) + tan²(b) – 2 tan(c) tan(b) cos (α) = sec²(c) + sec²(b) – 2 sec (c) sec (b) cos (a)   …. (9)

Tuttavia, ricordiamo, dalla volta scorsa, che:

sec²(c) = 1 + tan²(c)

e

sec²(b) = 1 + tan²(b)

Sostituendo nella (9) si ha:

tan²(c) + tan²(b) – 2 tan(c) tan(b) cos(α) = 1 + tan²(c) + 1 + tan²(b) – 2 sec (c) sec (b) cos (a)

e, ancora:

- 2 tan(c) tan(b) cos(α) = 2 – 2 sec(c) sec(b) cos(a)

- sen(c) sen(b) cos(α)/(cos(c) cos(b)) = 1 –  cos(a)/(cos(c) cos(b))

- sen(c) sen(b) cos(α)/(cos(c) cos(b)) = (cos(c) cos(b) –  cos(a))/(cos(c) cos(b))

- sen(c) sen(b) cos(α) = cos(c) cos(b) –  cos(a)

sen(c) sen(b) cos(α) = - cos(c) cos(b) + cos(a)

cos(a) = cos(b) cos(c) + sen(b) sen(c) cos(α)           …. (10a)

La (10a) è chiamata prima formula fondamentale della trigonometria sferica.

Essa permette di ricavare la lunghezza di un arco conoscendo gli altri due e l’angolo tra essi compreso.

Ovviamente, cosa analoga può essere fatta per ogni lato del triangolo (chi vuole provare può divertirsi) e si ottengono le altre due formule del tutto simili (basta ruotare le lettere):

cos(b) = cos(c) cos(a) + sen(c) sen(a) cos(β)        …. (10b)

 cos(c) = cos(a) cos(b) + sen(a) sen(b) cos(γ)          …. (10c)

Dove gli angoli β e γ sono indicati nella Fig. 19.

 Può sembrare qualcosa di complicato, ma vi posso assicurare che è veramente utile per legare tra loro i vari sistemi di coordinate.