Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nell'articolo precedente , servendoci dell'insieme di Cantor, abbiamo dimostrato che , ovvero che la cardinalità dell'insieme delle parti di N è minore o uguale a quella di R, ovvero c , la potenza del continuo. Vogliamo ora trovare la diseguaglianza opposta, ovvero  , per poter poi concludere,  grazie al Teorema di Bernstein , che

.

Prima un richiamo alle proprietà dei numeri reali, in particolar modo all'assioma di Archimede, che più che un assioma è una conseguenza della continuità dei numeri reali. Abbiamo infatti dimostrato QUI , che  comunque si scelgano due numeri e, a reali positivi esiste un numero naturale n tale che n*e>a. Descriviamo l'assioma con un esempio:

a=1, e=0,00000003

1/e=33333333,33.... per avere n*e>1  basta prendere n > 33333333 +1.Possiamo anche dire che per l'assioma , dati due numeri reali qualsiasi, è sempre possibile trovare un multiplo dell'uno che sia maggiore dell'altro.

Vogliamo ora vedere una importante conseguenza di questo assioma; comunque scelga due numeri reali, esiste sempre un numero razionale che sta in mezzo ai due numeri.

Detto formalmente, per ogni x,y appartenenti ad R, con x<y ,esiste un q appartenente a Q , tale che x<q<y. Osserviamo che possiamo limitare la dimostrazione al caso in cui 0<x<y; infatti ci sono altri due casi:

1)x<0<y; ma in questo caso il numero razionale lo abbiamo già trovato (o è un numero razionale)

2)x<y<0; ma allora -x>-y>0, ovvero o<-y<-x.  Ci riduciamo al caso in cui i due numeri siano entrambi positivi; se riusciamo a dimostrare che 0<-y<q<-x, allora x<-q<y<0.

Dimostrazione

Siamo nel caso 0< x<y, allora y-x>0; possiamo allora applicare l'assioma di Archimede; consideriamo e=y-x, a=1; allora esiste un numero naturale tale che , ossia , , da cui:

1 )  ;

Consideriamo adesso il numero reale  e l'insieme

H={h naturali tali che }

H non è vuoto; infatti sempre per l'assioma di Archimede, esiste   tale che

Per il principio del buon ordinamento dei naturali, che abbiamo visto QUI  l'insieme H (come ogni altro insieme di numeri naturali) ammette minimo, chiamiamolo ; allora  , mentre  , perchè  non appartiene ad H, essendo      il minimo di H.

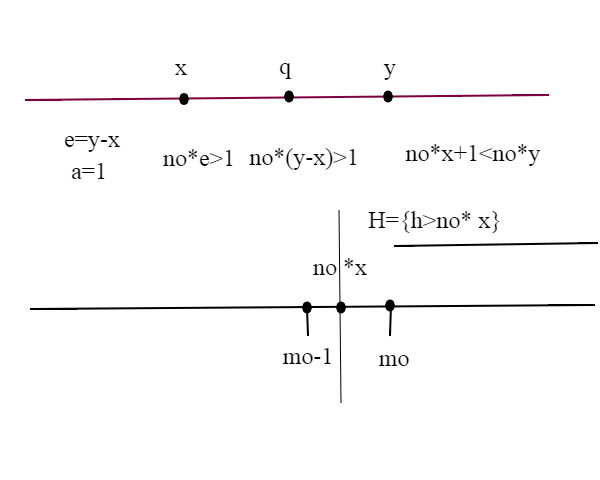
quindi:

 dove abbiamo usato la 1),cioè  nell'ultimo passaggio.

 ; dividiamo adesso entrambi i membri per :

  ma  essendo un rapporto fra numeri naturali è un numero razionale.

Quindi per quanto siano vicini x,y esiste sempre un razionale che sta in mezzo ai due.

Dimostriamo ora che 

Dato un numero reale x qualsiasi, consideriamo tutti i sottoinsiemi di Q, per cui, per ogni elemento q che vi appartiene, q<x. Questi sottoinsiemi sono un sottoinsieme  delle parti di Q ( e gli elementi di P(Q) sono tanti quanti , essendo Q numerabile, vedi appendice).

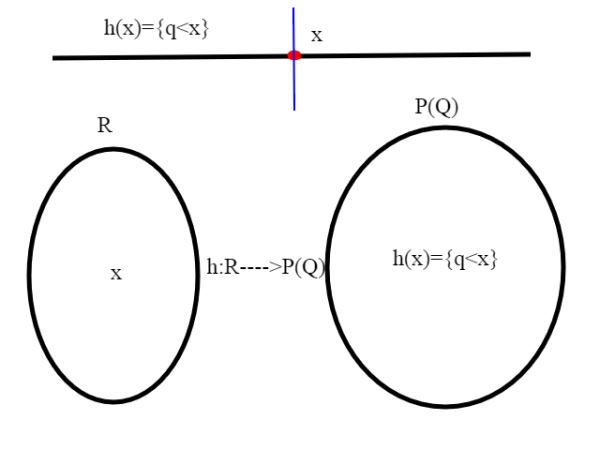
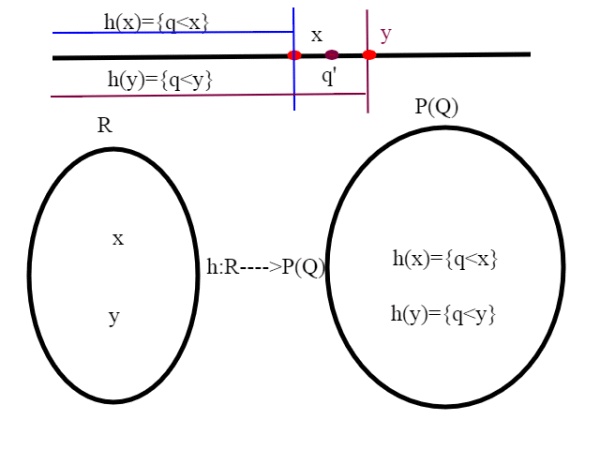
Chiamo quindi h l'applicazione che associa ad un numero reale x il sottoinsieme di P(Q) composto dai numeri razionali q tali che q<x, h: R--->P(Q); mi basta dimostrare che h è iniettiva. Se x,y sono due numeri reali diversi, possiamo supporre x<y; per quanto visto esiste q' tale che x<q'<y, quindi ho almeno un punto razionale che differisce negli insiemi di numeri razionali q<x, q<y che sono rispettivamente h(x) e h(y)  , ovvero h(x)<>h(y), quindi h è iniettiva, e . Ci basta questo per concludere,in base al teorema di Bernstein, e al risultato dell'articolo precedente, che 

Appendice

L'insieme delle parti di Q, P(Q) ha la stessa cardinalità dell'insieme delle parti di n, P(N), ossia |P(Q)|=.

Essendo Q numerabile, sappiamo che esiste una applicazione biunivoca , chiamiamola h:N--->Q

Vogliamo costruire una applicazione p:P(N)--->P(Q)

se N1 è un sottoinsieme  di N, N1={n1,n2...} definiamo p(N1)={h(n1),h(n2)...}

p è iniettiva.

Infatti, se consideriamo due sottoinsiemi di N  diversi, chiamiamoli N1 e N2 ,allora differiscono per almeno un elemento, sia n ,che per esempio sta in N1 ma non in N2. Ma allora se mando questi due sottoinsiemi in P(Q)  usando la p, ottengo due insiemi diversi, perchè h è iniettiva, quindi h(n)  sta in h(N1), ma non in h(N2).

p è suriettiva:

Se {q1,q2,..} è un sottoinsieme di P(Q), esistono n1,n2,.. tali che h(n1)=q1, h(n2)=q2. Quindi l'immagine p {n1,n2..} è proprio {q1,q2,..}.