Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Abbiamo spesso pensato al campo gravitazionale, generato da una grande massa, come a una enorme ragnatela (QUI), capace di catturare e gestire il moto di un piccolo corpo che gli si avvicini troppo. In parole povere stiamo parlando del problema dei due corpi, discusso non molto tempo fa (QUI). E’ ora di passare a una doppia ragnatela e vedere cosa è capace di fare. Parleremo di baricentro, di punti lagrangiani (QUI), di lobi di Roche (QUI) e tante belle cose che in parte già sappiamo, ma che è bene riassumere e trattare con maggiori dettagli.

Cerchiamo di costruire questa doppia ragnatela andando avanti a piccoli passi. La faremo girare attorno un punto molto particolare che conosciamo molto bene, ma che è meglio richiamare in modo più “formale”. Detto in altre parole, vogliamo affrontare il problema dei tre corpi, limitandoci alle sue soluzioni più “scaltre”.

Baricentro geometrico

Limitiamoci a un piano (ma non sarebbe difficile lavorare anche nelle tre dimensioni) e consideriamo un sistema di assi cartesiani x,y. Prendiamo un certo numero di punti P_i, individuati ovviamente dalle loro coordinate x_i,y_i, come mostrato in Fig. 1.

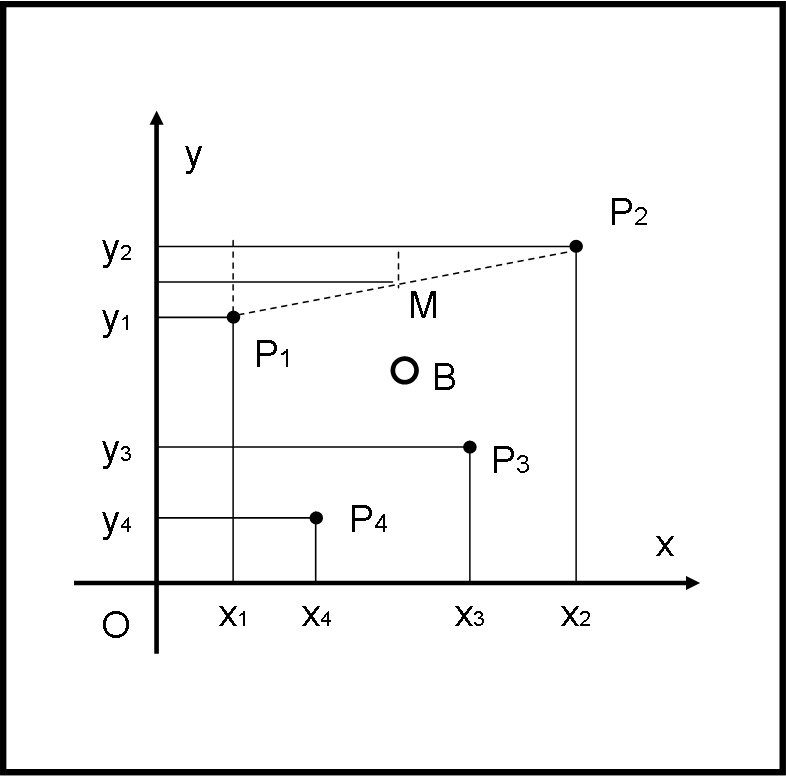
Ricordiamo, prima di tutto, cosa significa punto medio tra due punti o -se preferite- punto medio del segmento che unisce due punti. Sia esso, ad esempio il segmento P₁P₂. Beh, penso proprio che tutti sappiano che basta fare la media delle x e delle y e il punto, che ha come coordinate questi valori medi, è proprio il punto medio M. E’ la stessa cosa che si fa quando ci si chiede : “Qual è il valore medio tra 2 e 5?”. Non si fa altro che sommare i due numeri e dividere per due, ossia:

(2 + 5)/2 = 3.5

Nel caso di due punti basta allora fare la media delle loro x e delle loro y, ossia:

x_M = (x₁ + x₂)/2

y_M = (y₁ + y₂)/2

E’ immediato estrapolare il concetto a n punti, così come è immediato calcolare la media di n numeri… “Qual è il valore medio di  sei numeri come 2, 4, 8, 9, 14, 17 ?”. Ovvio:

(2 + 4 + 8 + 9 + 14 + 17)/6 = 44/6 = 7.3333…

Basta sommare i numeri e dividere per il loro numero totale.

Passando, allora al nostro piano cartesiano, basta scrivere (in modo generalizzato e per n punti qualsiasi):

x_B = (x₁ + x₂ + x₃ + …. + x_n)/n

y_B = (y₁ + y₂ + y₃ + …. + y_n)/n

Per passare allo spazio a 3 dimensioni basterebbe aggiungere:

z_B = (z₁ + z₂ + z₃ + …. + z_n)/n

In modo più compatto (ormai lo conosciamo bene dalle lezioni di matematica (QUI))

x_B = Σⁿ_{i = 1} x_i/n

y_B = Σⁿ_{i = 1} y_i/n

Questo punto B(xB,yB) viene chiamato baricentro geometrico dell’insieme di punti P_i.

Centro di massa

Per restare in campo matematico, potremmo adesso ragionare in un modo molto semplice. Consideriamo i numeri 1, 2, 4 e 5 (tanto per fare un esempio). Tuttavia, nella nostra serie di dieci numeri totali, qualcuno compare più di una volta. Il 2 compare due volte, il 4 due volte e il 5 cinque volte. Il valore medio diventa, perciò:

(1 + (2 + 2) + (4 + 4) + (5 + 5 + 5 + 5 + 5))/10 =  3.8

Potremmo anche scrivere:

(1 + 2(2) + 2(4) + 5(5))/10 = (1 + 4 + 8 + 25)/10 = 3.8

In parole molto semplici, abbiamo eseguito una media pesata. Ossia, se un certo numero o punto compare più volte, esso viene moltiplicato per il numero di volte che compare e poi si esegue la somma dividendo per il numero totale effettivo dei punti.

Ad esempio, passando al piano cartesiano, potremmo avere 3 volte il punto P₁(x₁,y₁), due volte il punto P₂ (x₂,y₂) e 5 volte il punto P₃(x₃,y₃). In totale 10 punti.

Sarebbe inutile sommare x₁ tre volte, x₂ due volte e x₃ cinque volte, basterebbe moltiplicare x₁ per 3, x₂ per 2 e x₃ per 5 e poi dividere per 10, ossia:

x_B = (3x₁ + 2x₂ +5x₃)/10

y_B = (3y₁ + 2y₂ +5y₃)/10

In poche parole, abbiamo ottenuto un baricentro diverso da quello dato dai tre punti P₁, P₂ e P₃, presi singolarmente, dato che ogni punto compare un certo numero di volte, ossia con un certo PESO.

Il nome “peso” ci aiuta a passare a un baricentro ben più importante, di tipo fisico, detto anche centro di massa.  Basta scrivere:

x_B = m₁x₁ + m₂x₂ + m₃x₃ + … + m_nx_n/(m₁ + m₂ + m₃ + … + m_n)

y_B = m₁y₁ + m₂y₂ + m₃y₃ + … + m_ny_n/(m₁ + m₂ + m₃ + … + m_n)

e, invece di vedere m_i come il numero di volte che compare un certo valore x_i (o y_i), si può pensare a m_i come alla massa del punto P_i.

Il baricentro o centro di massa di n oggetti puntiformi di massa diversa è dato quindi dalle relazioni:

x_B = Σⁿ_{i = 1} m_ix_i/M

y_B = Σⁿ_{i = 1} m_iy_i/M

dove M è la massa totale dei punti, ossia:

M = Σⁿ_{i = 1} mi

Due sole masse

Nel moto dei tre corpi, vi sono due masse che dominano la situazione, mentre la terza è considerata trascurabile, ne segue che il baricentro o centro di massa del sistema formato da due masse m₁ e m₂ si riduce semplicemente alle relazioni:

x_B = (m₁x₁ + m₂x₂)/(m₁ + m₂)

y_B = (m₁y₁ + m₂y₂)/(m₁ + m₂)

Se consideriamo le due masse poste lungo l’asse x (possiamo sempre sceglierlo in questo modo), la relazione si riduce alla prima delle due equazioni precedenti.

x_B = (m₁x₁ + m₂x₂)/(m₁ + m₂)

Possiamo trafficare un po’ con questa relazione…

x_B (m₁ + m₂) - m₁x₁ + m₂x₂    …. (1)

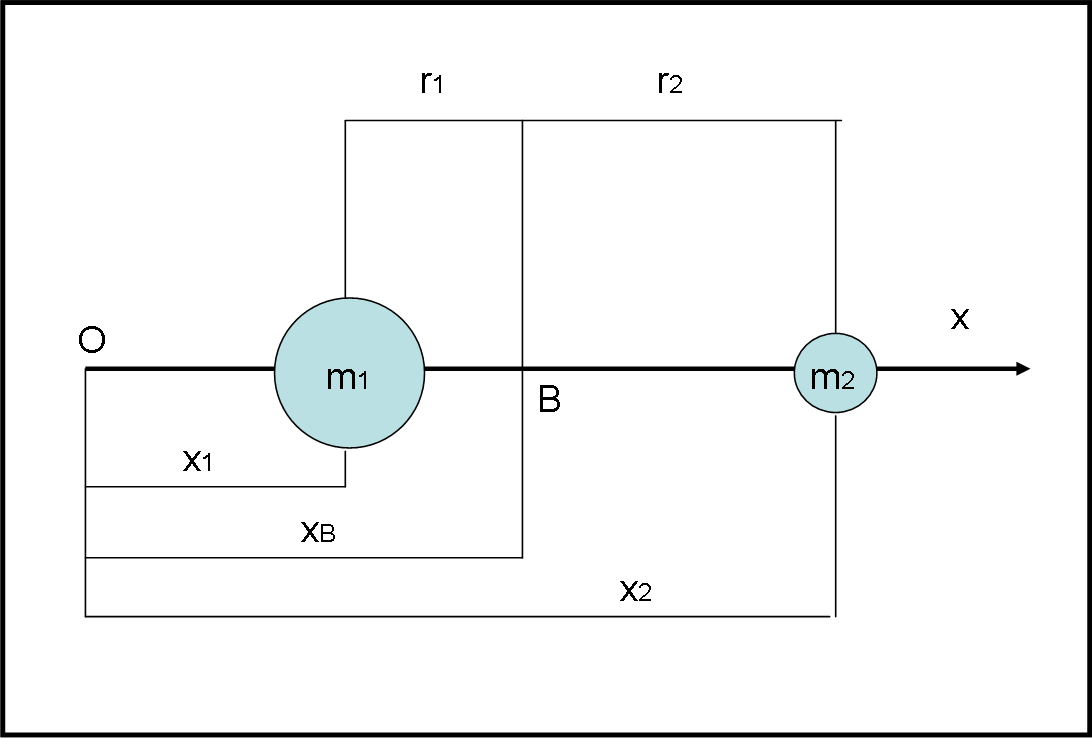
A questo punto, chiamiamo r₁ la distanza tra il punto P₁ e il centro di massa e r₂ la distanza tra il punto P₂ e il centro di massa. La Fig. 2 ci dice subito (avendo scelto un certo verso positivo) che:

x₁ = x_B - r₁

x₂ = x_B + r₂

Sostituendo nella (1)

x_B (m₁ + m₂) = m₁ (x_B  - r₁) + m₂ (x_B + r₂) = x_B(m₁ + m₂) - m₁r₁ + m₂r₂

semplificando:

- m₁r₁ + m₂r₂ = 0

m₁r₁ = m₂r₂

r₁/r₂ = m₂/m₁

che è la formula più conosciuta per definire il baricentro tra due masse distinte. Essa dice, in pratica, che la distanza dal centro di massa o baricentro dalle due masse è inversamente proporzionale ad esse. Il che vuole anche dire che più una massa è grande rispetto all’altra e più il baricentro del sistema si avvicina alla prima. Ad esempio, nel caso del Sole e della Terra, il baricentro cade all’interno della superficie del Sole.

Un po’ di vettori e un piccolo QUIZ grafico

La trattazione fatta finora ha fatto uso di coordinate cartesiane, ma, in generale, può essere più utile e “fisico” considerare le distanze vettoriali r_i dei punti rispetto a una certa origine O (x_i, y_i sono le sue componenti), come mostrato in Fig. 3.

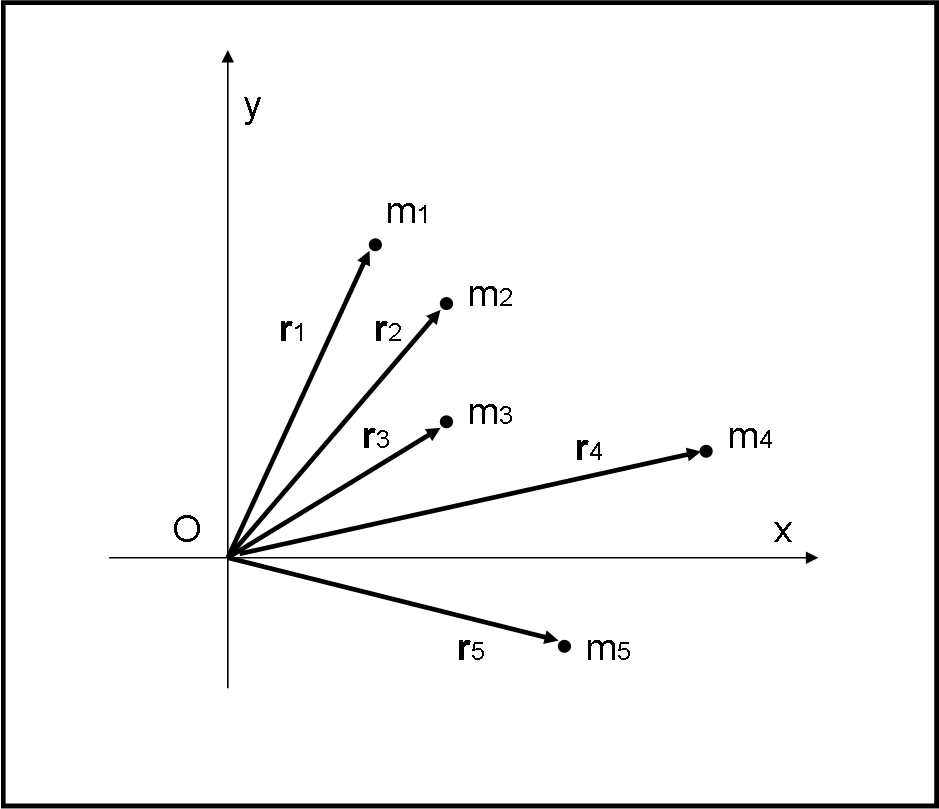
In tal modo è molto semplice e intuitivo calcolare la somma delle singole masse moltiplicate per i relativi vettori posizione r_i: essa non è altro che una somma vettoriale che si risolve con il metodo del parallelogramma (QUI), applicato via via a tutti i vettori. Immaginiamo, ad esempio, che le masse siano tutte uguali a uno. I  moduli dei singoli vettori sono, perciò, esattamente uguali alle distanze tra origine e punto finale P_i. La formula che dona la posizione del centro di massa diventa:

r_B = Σⁿ_{i = 1} r_i/n

La massa M diventa, ovviamente, 1 x n = n (numero di punti)

Vediamo un esempio grafico in Fig. 4. Sono stati disegnati sei punti di massa unitaria. Domanda: Come fareste a trovare vettorialmente e soltanto graficamente il loro baricentro, nel modo più rapido? Notate che non ho imposto nessuna origine…

Oggetto rigido esteso: un po’ di integrali

L’importanza del baricentro risulta -forse- ancora più chiara quando si parla di un oggetto rigido esteso. Ricordiamo, ad esempio, che tutta la massa può essere considerata concentrata nel suo baricentro (QUI).

Questa affermazione ci porta automaticamente a definire il baricentro di un oggetto qualsiasi (non puntiforme). Basta dividere l’oggetto in tanti “pezzettini” di massa infinitesima dm e poi sommare tutte le masse, moltiplicate per il vettore posizione relativo, e dividerle per la massa totale (Fig. 5).

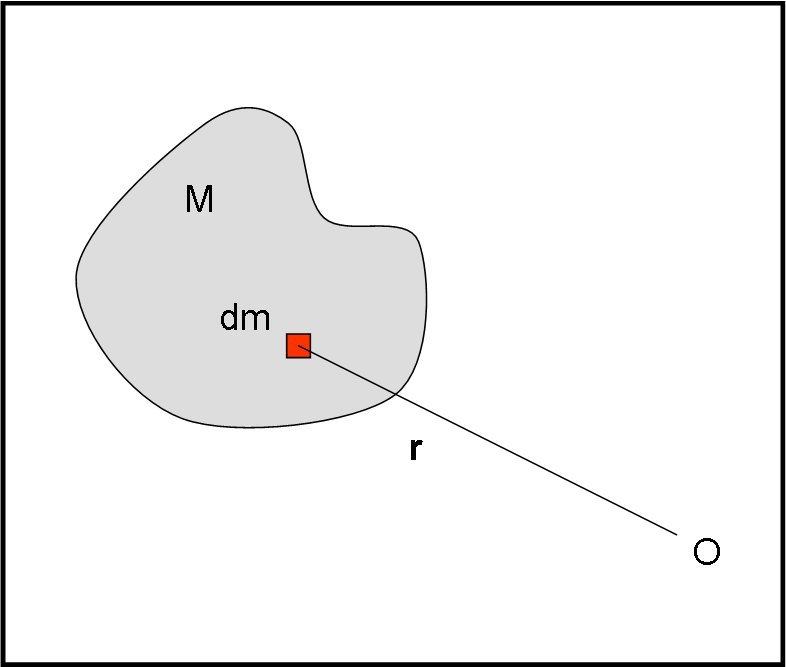
Per fare questo speciale tipo di somma ci viene in aiuto l’operazione di integrale (QUI).

In pratica, vengono considerati tanti volumetti dV che, considerando la densità δ costante, permettono di scrivere la massa dm come:

dm = δ dV

e, quindi, la somma di tutte le masse, moltiplicate per i vettori posizione, risulta:

δ ∫_V r dV

mentre  la massa totale è:

δ ∫_V dV

Ne segue che:

r_MB= ∫_V r dV/∫_V dV = ∫_V r dV/V

 

Ovviamente, la scelta della forma dei “pezzettini” di volume dV dipende molto dalla forma dell’oggetto in generale. Ma questo è tutto un altro discorso… dato che se la figura è piana useremo un integrale doppio e se è a tre dimensioni, un integrale triplo…

Concludiamo, cercando di analizzare la differenza, se esiste, tra baricentro e centro di massa. Entrambi sono caratteristiche intrinseche dell’oggetto (o dell’insieme di punti), indipendenti da dove l’oggetto sia posizionato. Il baricentro di un gruppo di punti o di una figura geometrica dipende solo dalla dislocazione dei punti o dalla forma. Il centro di massa vede comparire la massa, assegnata a ogni punto o all’oggetto esteso. In entrambi i casi, se la densità è costante, tutto si riduce a un calcolo puramente geometrico. Baricentro e centro di massa sono del tutto equivalenti.

Baricentro fisico

Tuttavia, se un corpo viene immerso in un campo di forze come, ad esempio, quella gravitazionale, può succedere che l’oggetto in questione sia disposto in modo tale che i suoi “punti” subiscano una forza peso diversa.

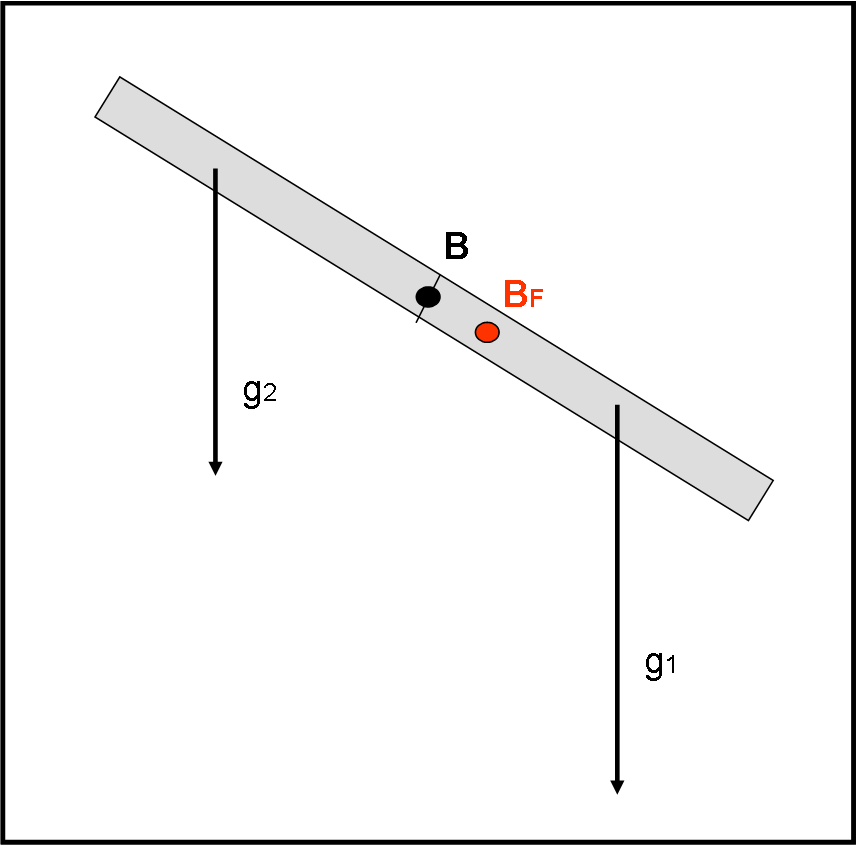
Immaginiamo una barra di ferro omogenea che cada verso la Terra, inclinata di un certo angolo rispetto alla verticale. Una sua parte subisce una gravità minore dell’altra e quindi il baricentro fisico si sposta verso la parte che avanza (vedi Fig. 6) e non coincide più con il centro di massa che deve rimanere sempre lo stesso, essendo una caratteristica intrinseca dell’oggetto. Tuttavia, questa situazione non ha veri risvolti pratici e possiamo, perciò, fare coincidere la definizione di baricentro con quella di centro di massa (sempre che la densità sia costante).

L’argomento baricentro non finisce certo qui, dato che la possibilità di concentrare tutta la massa di un corpo in questo punto veramente speciale permette di usarlo, come punto di riferimento fondamentale, nella descrizione dei vari moti. Ricordiamo, ad esempio, come il baricentro di un sistema stellare doppio si muova di moto rettilineo uniforme, mentre le stelle gli danzano intorno. Proprio a una situazione simile dobbiamo riferirci per parlare dei punti lagrangiani e di L4 e L5, in particolare.