Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Abbiamo imparato tante belle cose (che trovate QUI) sulla superficie sferica e, in qualche modo, l’abbiamo confrontata con una superficie piana, dove è molto più semplice lavorare. Tuttavia, ormai sappiamo cosa sono i cerchi massimi e i cerchi minori, così come sappiano riconoscere e risolvere un triangolo sferico. In poche parole, siamo in grado di trovare un sistema di riferimento tale che ci permetta di definire qualsiasi punto della sfera attraverso un paio di coordinate. Ovviamente, non può più essere un sistema di assi cartesiani, ma qualcosa che tenga conto delle caratteristiche essenziali della superficie sferica, dove si opera con angoli, che abbiamo descritto e collegato tra loro sia in modo intrinseco che estrinseco.

Abbiamo tutto e ci manca solo una sfera concreta su cui provare cosa abbiamo imparato. La prima che ci capita a tiro la conosciamo molto bene ed è la nostra Terra. No, non gridate allo scandalo: sappiamo molto bene che la Terra non è una sfera perfetta, ma per lo scopo che dobbiamo raggiungere in questa trattazione, è più che sufficiente. Analogamente, considereremo certe caratteristiche della sfera-Terra come immutabili nel tempo. Se avremo voglia, potremo, in seguito, cercare di andare più nel sottile, tenendo conto di molte variazioni che i manifestano su tempi abbastanza lunghi per noi umani o che comportano errori trascurabili, in prima approssimazione.

Prima di proseguire con l’introduzione di un sistema di coordinate sferiche terrestri, è bene richiamare un concetto sicuramente elementare e ovvio, ma che può essere di un qualche interesse per i meno preparati.

Sfera terrestre e sfera celeste

Facciamoci una domanda: “Qual è la differenza fondamentale tra una sfera come la Terra e una sfera come quella celeste?” Tra le tante, la più importante è che sulla superficie della Terra possiamo camminare e compiere misurazioni dirette, mentre su quella celeste è impossibile arrivare e la si può vedere solo dal suo centro e misurare gli angoli che separano i suoi punti. Questa banale, ma fondamentale differenza, la vediamo nella Fig. 1

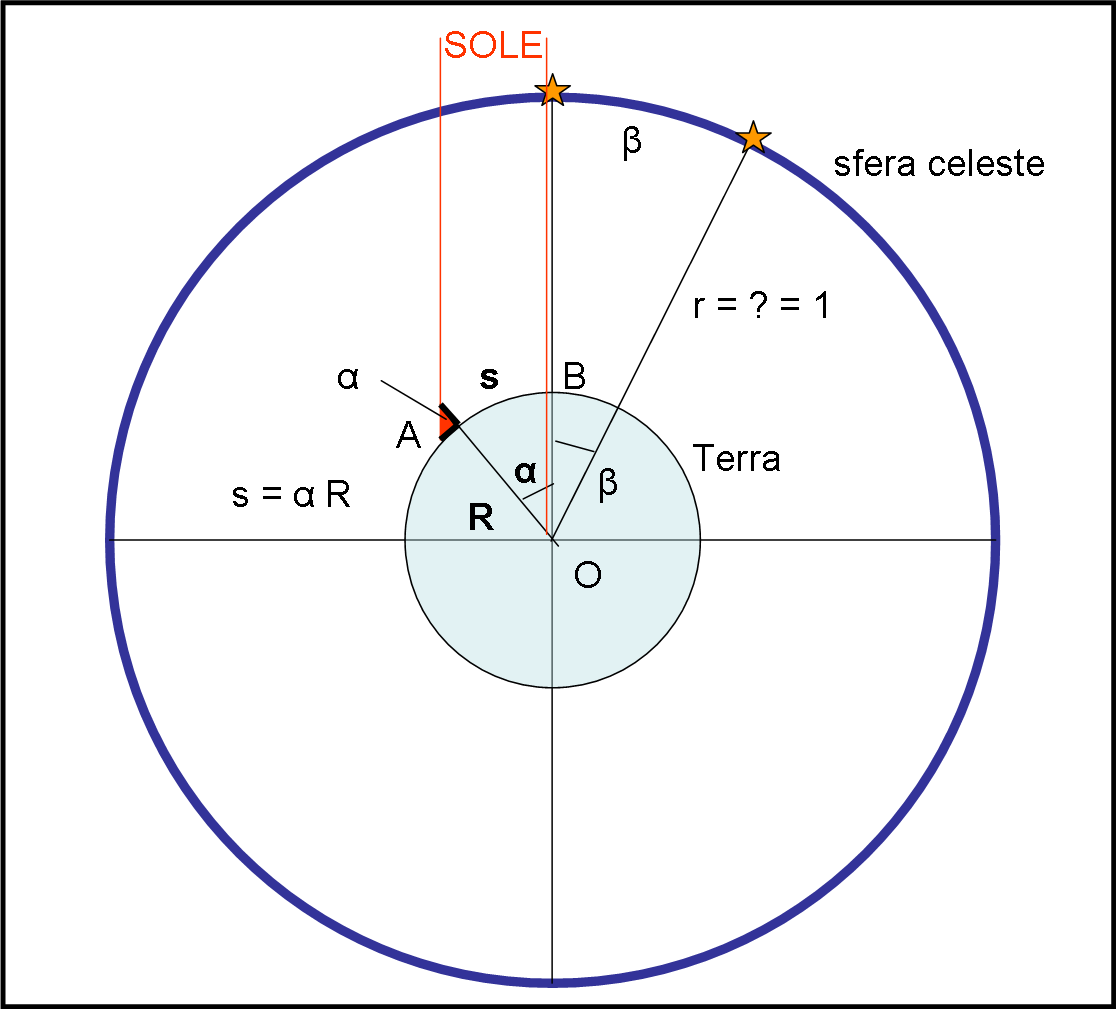
Traducendo il tutto in qualche formuletta, possiamo dire che potendo calpestare la Terra è possibile misurare la distanza, in chilometri, dell’arco di cerchio s e riuscire a determinare la misura della circonferenza, da cui il raggio R e l’angolo α, corrispondente all’arco s. Infatti:

α : s =  360 : 2πR

da cui:

α = 360 s /2πR

Lavorando in radianti:

α = s/R

Quel genio di Eratostene

Ovviamente, vale anche il viceversa. Riuscendo a calcolare l’angolo α e misurando direttamente s si ricava nientemeno che il raggio della Terra che abbiamo sotto i piedi.

Sì, ma come misurare l’angolo α ? Possiamo mica andare e tornare fino al centro della Terra? Beh… non ce n’è bisogno. Basta pensare che la Terra è rotonda, che il Sole può considerarsi a una distanza praticamente infinita (raggi paralleli) e avere una mente di prima classe.

Notiamo quel triangolino rettangolo rosso relativo al punto A che compare in Fig.1. La parte verticale rispetto al suolo è un’asta rigida e quella tangente al suolo è l’ombra dell’asta. Due cose che si misurano facilmente. Se si riesce a misurare anche la distanza s, magari a dorso di un dromedario dal passo molto regolare, e sapendo che in B il Sole è esattamente sulla verticale del luogo, il gioco è fatto.

Il triangolino rosso ci regala l’angolo α (angoli alterni interni di rette parallele tagliate da una trasversale) che, insieme al percorso del dromedario s, ci permette di calcolare la circonferenza della Terra (e/o il suo raggio) con un errore inferiore al 5%!

Quando? pochi secoli fa! No, cari amici, nel terzo secolo avanti Cristo, per merito di un tale Eratostene di Cirene, che non avrà avuto cellulari o telescopi, ma che aveva sicuramente una testa di prima categoria che nel mondo di oggi sarebbe veramente preziosa e rara!

Torniamo a noi… La sfera celeste, invece, la vediamo dal di dentro e da molto lontano. Anzi, la sua distanza è indeterminata. Tutto ciò che possiamo fare è porre questa distanza (il raggio della sfera) uguale a uno e accettare di misurare le distanze tra le stelle come archi di cerchio (massimo!) a cui assegnare il valore dell’angolo β espresso in radianti.

Coordinate geografiche

Fatte queste dovute premesse, rivolgiamoci alla Terra e creiamo su di lei un “comodo” reticolato che ci permetta di identificare ogni suo punto attraverso una coppia di coordinate sferiche. Il vantaggio è enorme…

La Fig. 2 ci mostra una sfera perfetta. La prima cosa da fare è definire un suo cerchio massimo. Niente di più facile. Ve ne sono infiniti: l’importante è che essi siano generati dall’intersezione tra la superficie sferica e un piano qualsiasi che passi per il suo centro C.

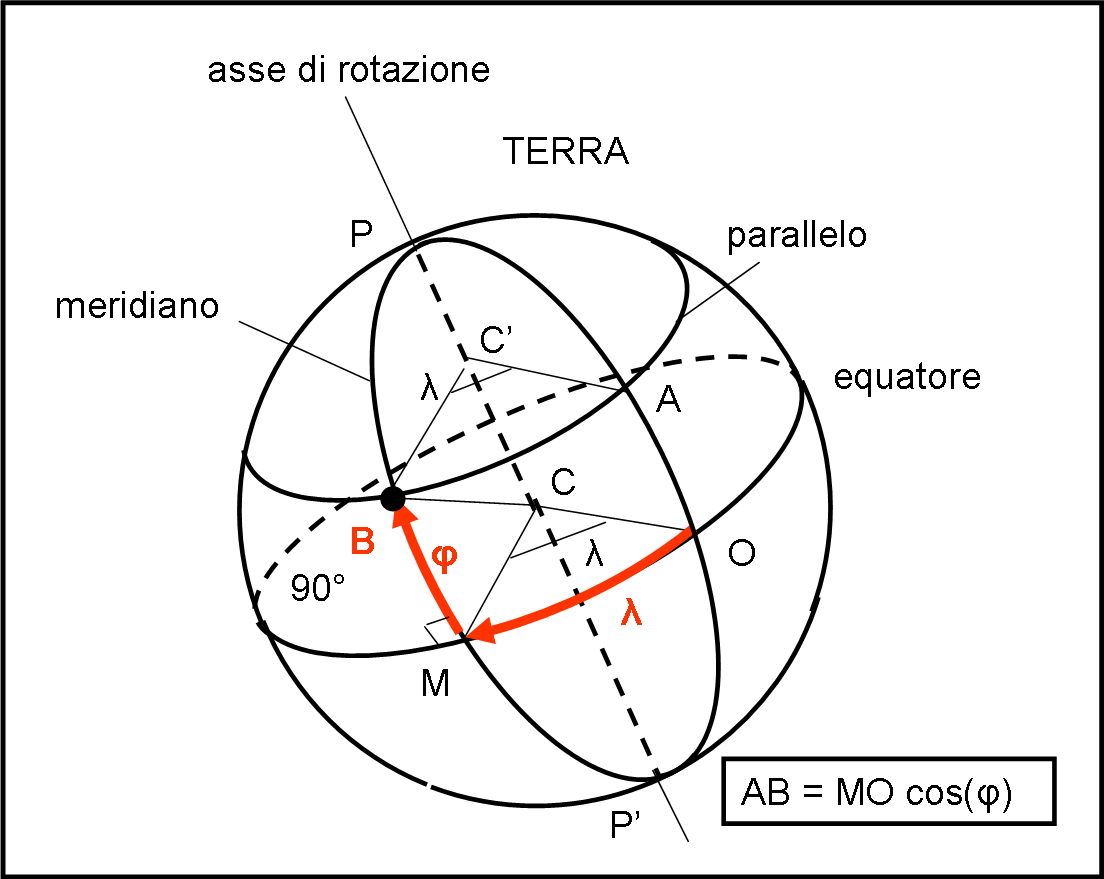
Scegliamone uno a caso, quello che passa per i punti M e O. Definito il cerchio massimo è anche facile definire una retta (estrinseca, ossia tracciata nello spazio a tre dimensioni) che sia perpendicolare al piano che lo ha generato.

Questa retta incontra la sfera in due punti P e P’. Questi punti sono estremamente particolari, dato che tutte le  rette (intrinseche, ossia che siano “rette” per un abitante della superficie sferica) perpendicolari al cerchio massimo devono passare per P e P’. In altre parole, questo fatto ci dice che tutte le rette intrinseche della superficie (cerchi massimi) si incontrano sempre in due punti antipodali (ossia che distino tra di loro di un arco uguale a π).

Possiamo divertirci a tracciare tutte le rette di questo tipo e sceglierne una in particolare, ad esempio quella che passa per O. Ribadiamo, ancora, che questa retta intrinseca non è altro che un cerchio massimo per una visione estrinseca. Tutti i piani che hanno generato i cerchi massimi estrinsechi che passano da P e P’ devono avere in comune la retta estrinseca PP’: siamo di fronte a un fascio di piani aventi come asse la retta PP’, vedi QUI).

A questo punto, siamo tranquilli che, muovendoci lungo il cerchio OM e lungo un qualsiasi cerchio PP’, stiamo percorrendo le traiettorie di minima distanza tra due punti, ossia dei cerchi massimi.

Come abbiamo già detto scegliamo il cerchio massimo POP’ come cerchio massimo di riferimento per le nostre coordinate sferiche, ossia per dare un nome e un cognome a ogni punto della superficie sferica nella nuova geometria.

Consideriamo un certo punto B e tracciamo il cerchio massimo PB che interseca il cerchio massimo OM in M. I due cerchi massimi sono tra loro perpendicolari per costruzione. Definiamo, come prima coordinata λ di B, l’arco di cerchio massimo OM.

Arrivati in M, portiamoci sul cerchio massimo MB fino a giungere in B. L’arco di cerchio massimo MB è la seconda coordinata φ del punto B, che viene perciò identificato come B(φ, λ).

Notiamo subito due punti fondamentali.

La coordinata λ è l’angolo formato dai due piani PCO e PCM. Ne segue che anche l’angolo BC’A è uguale a λ. Tuttavia, non confondiamoci pensando che λ sia anche l’arco AB. Esso non appartiene a un cerchio massimo e lo sarebbe solo se C’ coincidesse con C.

D’altra parte l’arco di cerchio AB non è un cerchio massimo dato che il piano che lo genera, parallelo al piano che genera OM, non passa per il centro della sfera. La lunghezza dell’arco AB è, però, facilmente ottenibile con una della formule che abbiamo ricavato per la trigonometria sferica (QUI) e dipende dall’angolo BCM (in particolare dal suo coseno):

AB =  OM cos(φ)

Si può, però, dire che tutti punti che stanno sul cerchio minore AB hanno lo stesso valore di φ. Risulta, invece, che tutti i punti dei cerchi massimi del tipo PBP’ hanno la stessa λ.

A questo punto, possiamo permetterci di smettere con la generalizzazione e considerare, come piano che contiene il cerchio massimo OM, quello dell’equatore terrestre. Ne seghe P e P’ diventano il Polo Nord e il Polo Sud (l’asse PP’ è l’asse di rotazione della Terra).

I cerchi massimi che passano per P e P’ prendono il nome di meridiani, mentre i cerchi minori che hanno la stessa coordinata φ sono detti paralleli. Per concludere, diciamo ancora che φ si chiama latitudine del luogo B e λ si chiama longitudine.

La prima varia tra 0° e 90° ed è positiva andando verso il Polo Nord e negativa andando verso il Polo Sud. Ricordiamo che il meridiano di riferimento (λ = 0), ossia POP’, è stato scelto come quello che passa per l’osservatorio di Greenwich in Inghilterra. La longitudine varia tra 0° e 180° e le si aggiunge Est od Ovest a seconda del verso. In altre parole, se ponendosi sul Polo Nord si va in verso orario si va verso Ovest, mentre se si va in verso antiorario si va verso Est. Sui punti Est e Ovest ci torneremo tra non molto…

Ridendo e scherzando, abbiamo introdotto le coordinate geografiche di un luogo qualsiasi della Terra.

Alcuni punti hanno coordinate del tutto speciali. Ad esempio, i due poli hanno latitudine + o – 90° e longitudine indeterminata. I punti dell’equatore hanno invece latitudine uguale a zero. Chi sta sul meridiano di Greenwich ha sempre longitudine uguale a zero, qualsiasi sia la sua latitudine.

Il fatto che la Terra ruoti attorno al suo asse ha poca importanza per le coordinate geografiche. Per come sono state definite, rimangono sempre le stesse in qualsiasi ora del giorno.

Tuttavia, il meridiano di riferimento ruota insieme alla Terra e quindi un orologio che sia posto sul meridiano di riferimento impiegherebbe 24 ore a compiere un giro completo e quindi indicherebbe ore diverse in diversi istanti della sua rotazione. Ogni altro meridiano lo seguirebbe o lo precederebbe in modo solidale e quindi il tempo scorrerebbe in modo analogo, anche se con una differenza rispetto a lui.

Questa differenza, espressa in ore, minuti e secondi è la differenza in longitudine tra i meridiani espressa in gradi, primi e secondi. In altre parole, la longitudine può essere benissimo espressa in ore, minuti e secondi tenendo presente la relazione:

24 ore = 360°, ossia:

1 ora = 15°.

QUI trovate tutti gli articoli su questo argomento