Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Questo articolo è un piccolo capolavoro di logica ed eleganza (non certo per merito mio…). Vi invito a leggerlo senza paura. Esso presenta la determinazione dei punti lagrangiani L₄ e L₅, nel modo più generale possibile, seguendo la strategia illustrata nel 1999 da I. Vorobyov dell’Università di Vienna. Un metodo di una semplicità disarmante, che io ho solo cercato di arrangiare in modo veramente elementare (matematica e geometria delle scuole medie).

Come abbiamo già detto varie volte, i punti lagrangiani, da un punto di vista fisico, sono strettamente collegati alle superfici equipotenziali di due corpi rotanti, ossia la ormai famosa doppia ragnatela, di cui parleremo nell’ultima parte. Essi sono gli unici cinque punti di equilibrio del sistema rotante: un oggetto posto in uno di essi, mantiene una posizione fissa rispetto alle due masse predominanti. Il sistema di riferimento in cui definirli è, perciò, quello rotante. Le forze in gioco sono, di conseguenza, quelle attrattive delle masse e quella centrifuga.

I punti L₁, L₂ e L₃ sono, in qualche modo, “facilitati” (QUI), dato che sono situati lungo la retta che unisce le due masse. Gli ultimi due, invece, si trovano ben distanti da questa linea e nemmeno Lagrange stesso avrebbe mai pensato che la sua soluzione matematica potesse avere una conferma fisica, data dai celebri asteroidi troiani e greci di Giove. Non solo i punti esistono e sono stabili, ma sono anche occupati fisicamente da corpi celesti in carne e ossa (ops… in terra e ghiaccio).

Prima di passare alla determinazione a cui si accennava prima, possiamo facilmente dimostrare che, effettivamente, la posizione ai vertici di un triangolo equilatero (in cui due vertici sono occupati dalle masse M₁ e M₂) soddisfa le condizioni richieste. Tuttavia, è una soluzione “di comodo”, perché non ci dice se possono esistere altri punti con le stesse caratteristiche.

Consideriamo la Fig. 1 in cui abbiamo disegnato due masse M₁ e M₂ e una piccola massa m posta proprio in modo da formare un triangolo equilatero con le altre due.

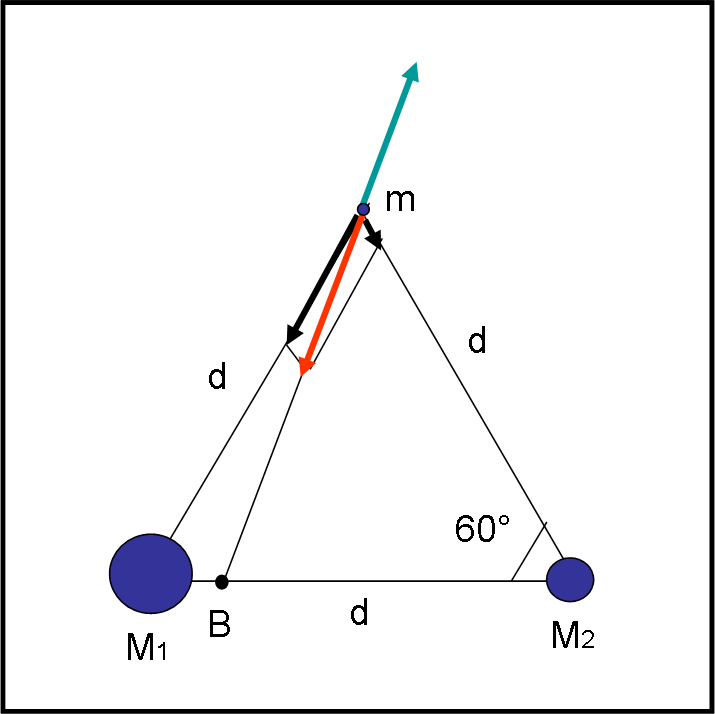
La massa m è attratta da entrambe e si trova alla stessa distanza da loro. Le forze agenti su di lei sono, perciò, direttamente proporzionali alle due masse M₁ e M₂. Ne segue che la composizione delle due forze è diretta verso il baricentro B. Dato che il sistema ruota attorno a B, la forza centrifuga che agisce sulla massa m controbilancia l’attrazione gravitazionale, assicurando la stabilità della posizione. Questa è però una dimostrazione “ a posteriori”. Inoltre, è ben chiaro che abbiamo considerato un sistema del tutto particolare, in cui il centro di massa stia sulla congiungente le due masse M₁ e M₂.

E se le tre masse fossero comparabili? In realtà, la soluzione visualizzata comunemente per i punti L₄ e L₅ si riferisce quasi sempre al caso di Giove e del Sole, in cui il baricentro è praticamente coincidente con quest’ultimo. Una figura ormai di uso comune… ma la configurazione può essere molto più generale ed è interessantissimo seguirne la trattazione, che è poi quella proposta e risolta dallo stesso Lagrange. Penso che anche i più esperti la troveranno illuminante e -forse- inaspettata.

Al di là dell’interesse matematico e fisico del risultato, seguiamola passo dopo passo per renderci conto di come si possano spiegare concetti anche difficili attraverso una serie di passaggi logici veramente elementari, a patto che vi sia dietro un cervello brillante. L’equazione “grande intelligenza = grande complessità” non è assolutamente obbligatoria (Feynman insegna). Come dicevo, il merito va tutto a Vorobyov e alla sua genialità: io ho solo cercato di semplificare e rendere ancora più immediata la trattazione, per renderla veramente godibile da TUTTI, amanti e non amanti della matematica.

Consideriamo tre corpi di massa m₁, m₂ e m₃ (la generalizzazione è massima) che NON stiano sulla stessa linea, ma che rivolvano con la stessa velocità angolare attorno a un certo punto O, su circonferenze ovviamente concentriche (il centro è lo stesso…). La situazione, mostrata in Fig. 2, simula perfettamente quella di un corpo “solido” che ruoti attorno a un asse, un corpo formato da un centro e da tre “barre” fisse che lo colleghino alle tre masse o, se preferite, un triangolo qualsiasi che giri attorno a un punto interno.

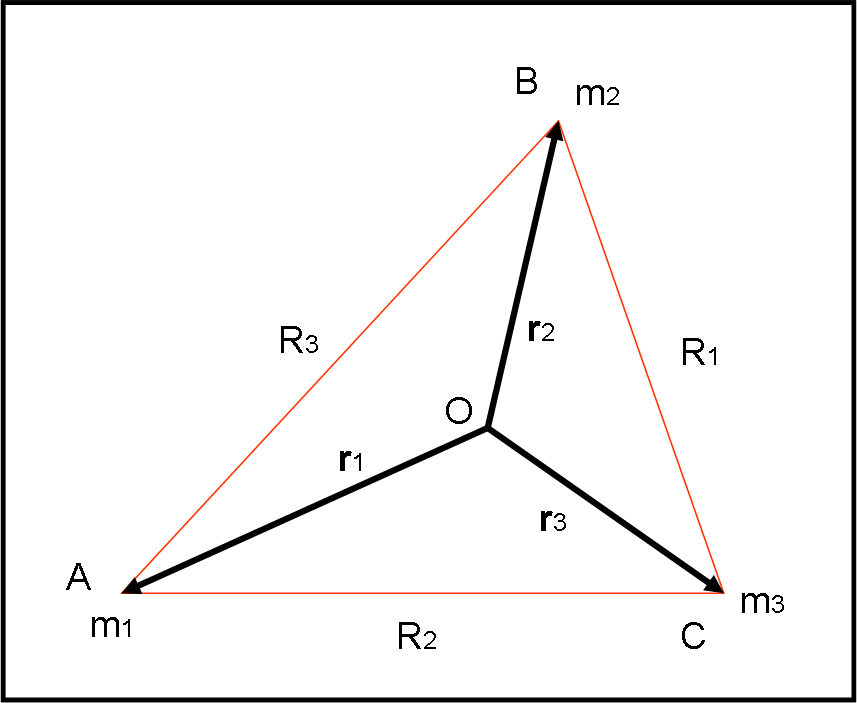
Ci chiediamo: “E’ possibile questa configurazione? E, se sì, sotto quali condizioni?”

Nel sistema rotante ciascuna massa m_i deve rimanere in equilibrio. In poche parole, vogliamo che il triangolo non muti la sua forma durante la rotazione.

Ogni singolo corpo è soggetto alle forze attrattive degli altri due corpi. Esse sono date da:

F₁ = F₁₂ + F₁₃

F₂ = F₂₃ + F₂₁

F₃ = F₃₁ + F₃₂

In parole povere, abbiamo solo detto che la forza attrattiva che subisce ogni massa m_i è la somma delle forze attrattive che m_j e m_k esercitano su di lei (sono ovviamente somme vettoriali). Tutte queste forze F_ij sono ovviamente dirette lungo i lati  R_k corrispondenti,

Il modulo della generica forza vale (legge di gravitazione di Newton):

│F_ij│= G m_im_j/R_k²                  (modulo della generica forza F_ij)

I tre corpi, però, devono anche ruotare con la stessa identica velocità angolare ω attorno a O. Sono perciò soggetti alle forze centrifughe F_Ci (dirette secondo OA, OB, e OC) date da (QUI):

F_C1 = m₁ω²r₁

F_C2 = m₂ω²r₂                  …. (1)

F_C3 = m₃ω²r₃

Ogni corpo deve essere in equilibrio nel sistema rotante, ossia la somma di tutte le forze agenti su di esso deve essere uguale a ZERO, ossia:

F₁ + F_C1 = 0

F₂ + F_C2 = 0

F₃ + F_C3= 0

O, ancora:

F₁₂ + F₁₃ + F_C1 = 0

F₂₃ + F₂₁ + F_C2 = 0

F₃₂ + F₃₁ + F_C3 = 0

Sommando le tre equazioni, si ha:

F₁₂ + F₁₃ + F₂₃ + F₂₁ + F₃₂ + F₃₁ + F_C1 + F_C2 + F_C3 = 0

Tuttavia, per il terzo principio della dinamica, si ha:

F₁₂ = - F₂₁

F₁₃ = - F₃₁

F₂₃ = - F₃₂

Abbiamo solo scritto che se m_i agisce su m_j con una certa forza gravitazionale, m_j deve agire su m_i con una forza uguale e contraria.

Semplificando si ha:

F_C1 + F_C2 + F_C3 = 0

Ricordando le (1)

m₁ω²r₁ + m₂ω²r₂ + m₃ω²r₃ = 0

Dato che ω non può essere uguale a zero, possiamo scrivere:

m₁r₁ + m₂r₂ + m₃r₃ = 0            …. (2)

Ricordando la definizione di baricentro o centro di massa, rispetto a una certa origine O (QUI):

r_B = Σ³_{i = 1} m_ir_i/M

si ha che se r_B = 0, come dice la (2), il punto O deve essere il baricentro del sistema delle tre masse m₁, m₂ e m₃.

In realtà, questo risultato non fa altro che confermare che, se in un sistema di corpi le uniche forze sono quelle che si esercitano tra di essi, il baricentro deve rimanere fisso. Ossia, il punto O, attorno a cui avviene la rivoluzione dei tre corpi, non può muoversi e quindi DEVE essere il baricentro del sistema.

Appurato questo fatto importantissimo, possiamo passare alla seconda parte dell’articolo, dove traffichiamo un po’ con i vettori. La figura di riferimento è adesso la Fig. 3 che è uguale a quella precedente, tranne qualche piccola freccetta. Notiamo che i vettori R₂ e R₃ puntano entrambi verso m₁

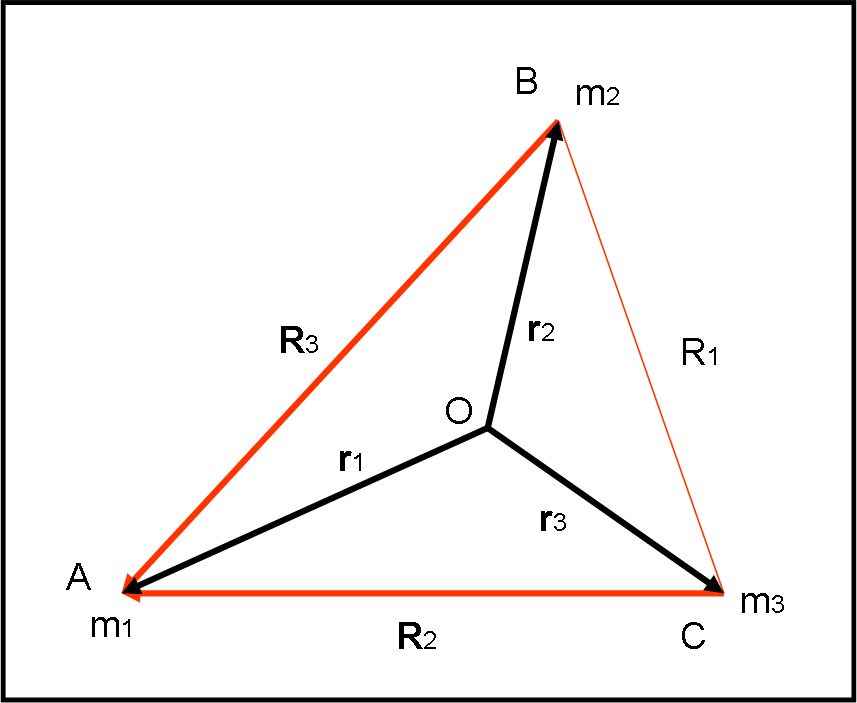
Sappiamo benissimo come sommare dei vettori, quindi non vi è nessun problema a scrivere:

r₁ = r₂ + R₃

ma anche:

r₁ = r₃ + R₂

Moltiplichiamo la prima equazione per m₂, la seconda per m₃ e poi le sommiamo :

m₂r₁ + m₃r₁ = m₂r₂ + m₂R₃ + m₃r₃ + m₃R₂        …. (3)

Dalla (2) abbiamo:

m₂r₂ + m₃r₃ = - m₁r₁

Sostituendo nella (3):

m₂r₁ + m₃r₁ = m₂R₃ + m₃R₂ - m₁r₁

m₂r₁ + m₃r₁ + m₁r₁= m₂R₃ + m₃R₂

r₁(m₁ + m₂ + m₃) = m₂R₃ + m₃R₂

Da cui si ricava:

r₁ = (m₂R₃ + m₃R₂)/(m₁ + m₂ + m₃)

Adesso, facciamo bene attenzione. Il vettore r₁ è la somma di due vettori, ossia:

ρ₂ = m₃ R₂/(m₁ + m₂ + m₃)

e

ρ₃ = m₂ R₃/(m₁ + m₂ + m₃)

In modo compatto:

r₁ = ρ₂ + ρ₃

Ragioniamo sopra questo semplice, ma fondamentale risultato.

Innanzitutto, si può affermare che ρ₂ ha la stessa direzione di R₂ così come ρ₃ ha la stessa direzione di R₃. I vettori differiscono, infatti, solo per il modulo. Inoltre, la somma vettoriale di ρ₂ e ρ₃ deve proprio essere r₁. Ne segue che i due nuovi vettori possono essere indicati facilmente in blu nella Fig. 4.

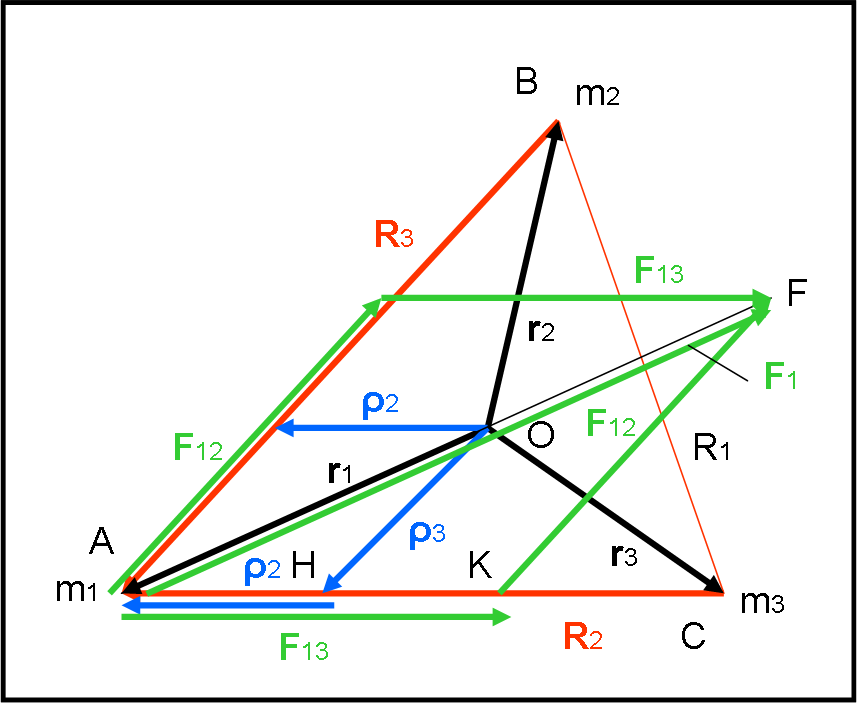
Ora viene la parte più “astuta”.

Passiamo ai vettori delle forze gravitazionali agenti su m₁. La forza F₁₂ (relativa a m₂) deve agire lungo il lato R₃. La forza F₁₃ (relativa a m₃) deve agire lungo il lato R₂. In altre parole, le due Forze sono parallele ai vettori ρ₃ e ρ₂. Disegniamo queste due forze, F₁₂ e F_13, in verde.  Il modulo possiamo anche disegnarlo a caso (dipende dalle masse), ma è sicuramente vero che la risultante F₁ delle due forze F₁₂ e F_13, deve essere diretta da m₁ verso il baricentro (il moto avviene attorno a lui).

Consideriamo i triangoli AOH e AFK. Essi sono simili (i tre angoli sono uguali).

I loro lati, però, sono proprio i vettori forze F₁₂ e F₁₃ e i vettori ρ₃ e ρ₂. Ne segue che i loro moduli devono essere in proporzione:

F₁₂/ρ₃ = F₁₃/ρ₂

Scrivendoli per esteso:

Gm₁m₂/R₃²: m₂R₃/(m₁ + m₂ + m₃) = Gm₁m₃/R₂²: m₃ R₂/(m₁ + m₂ + m₃)

(Gm₁m₂/R₃²) (m₃ R₂/(m₁ + m₂ + m₃)) = (Gm₁m₃/R₂²) (m₂R₃/(m₁ + m₂ + m₃))

Gm₁m₂m₃ R₂/ R₃² (m₁ + m₂ + m₃) = Gm₁m₃ m₂ R₃/R₂² (m₁ + m₂ + m₃)

Semplificando:

R₂/R₃² = R₃/R₂²

R₂³ = R₃³

Ossia:

R₂ = R₃

Se qualcuno vuole divertirsi, può rifare l’ultima parte di calcolo cambiando la massa di riferimento: invece di m₁ si può considerare m₂, con tutti i vettori relativi. Troverà, ovviamente, che:

R₁ = R₃.

Il triangolo ABC deve essere equilatero e O ne è il baricentro.

Alla domanda iniziale: “E’ possibile questa configurazione? E, se sì, sotto quali condizioni?”, possiamo rispondere senza esitazione: “Sì, la configurazione è possibile a patto che il centro di rotazione O sia il baricentro del sistema e che le tre masse occupino i vertici di un triangolo equilatero”.

Notiamo molto bene quanto la soluzione sia ben più generale di quella che viene comunemente riportata. Le tre masse sono qualsiasi e il triangolo ruota attorno al baricentro del sistema.

I troiani e i greci di Giove si trovano (quasi) esattamente nei pressi dei punti lagrangiani L₄ e L₅. In realtà, le loro orbite librano attorno a questi punti, in modo anche vistoso, ma il sistema complessivo mantiene la sua stabilità perfetta.

Questo classico esempio è, però estremamente, particolare. Il baricentro O coincide praticamente con il Sole e, di conseguenza, il pianeta e i due gruppi di asteroidi rivolvono attorno al Sole lungo la stessa orbita (Fig. 5).

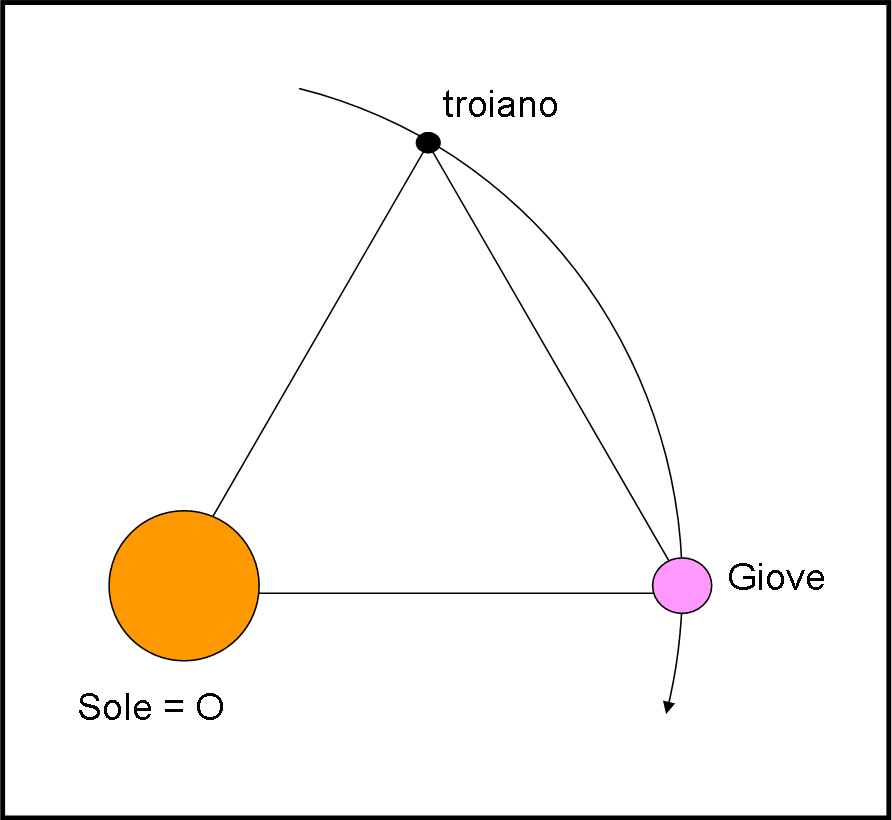
Chissà che, prima o poi, non si trovi un sistema stellare triplo che rappresenti l’esempio più generale della geniale soluzione (particolare) di Lagrange, per il problema dei tre corpi…

Esistono anche altri metodi per determinare L₄ e L₅, soprattutto analitici. Essi sono estremamente “noiosi” e contorti. Ho preferito presentare solo quello vettoriale, molto più semplice e geniale.

La prossima volta ci occuperemo direttamente della doppia ragnatela gravitazionale e vedremo la faccenda da un punto di vista decisamente più fisico.