Sono appena tornato da una settimana di ferie e mi sono trovato due commenti ai quali vorrei rispondere in modo corale, soprattutto per far capire ancora meglio lo spirito del circolo (e certe sue caratteristiche) a chi lo ha seguito da poco tempo.

Dopo non poche perplessità ed esitazioni, Ciccio è riuscito a comprendere talmente bene la spiegazione di PapalScherzone su come mai Astericcio & co. stavano fluttuando in assenza di peso nella papalastronave, che ha deciso di approfondire l’argomento e ci ha chiesto di scrivere questa appendice dedicata a chi, come lui, è curioso e vuole saperne di più. Ed era talmente entusiasta che ha insistito per prendere parte attiva agli esperimenti che ora andremo ad analizzare (ma state tranquilli… lo abbiamo fatto saltare da una piccola altezza, in modo che non corresse il rischio di farsi male!).

Cosa c'è di meglio di una gita nello Spazio per apprezzare la meraviglia che ci circonda? I nostri piccoli ma sempre più saggi amici vivranno un'esperienza che, oltre a donare loro emozioni e divertimento, arricchirà il loro bagaglio di conoscenze e la loro capacità di riflettere e pensare con la propria testa. Per non parlare, poi, di una nuova stimolante amicizia!

Un popolo che inizia a vedere la luce, un altro che la sta spegnendo: a quale luce si riferisce Vin-Census? Forse quella di un perfetto ordine sociale e della fine di tutti i conflitti? Può darsi, ma potrebbe essercene una più importante...

In questi giorni si parla (abbastanza) di un pianeta che appartiene a un sistema triplo. I titoli si lanciano su situazioni da film di fantascienza e si pensa soltanto alla visione di tre albe e di tre tramonti e/o di un pianeta riscaldato da tre soli (non riporto le fonti, ma sono facili da recuperate). In realtà la situazione non è poi così strana e rappresenta un bellissimo problema dei tre corpi (e magari, in futuro anche dei quattro). Affrontiamolo, brevemente, sotto questo aspetto, ben più intrigante.
La seconda formula fondamentale è sicuramente la più “difficile” da ottenere. Non spaventatevi, però… sono solo passaggi matematici alla portata di tutti. Inoltre, si può notare come piccoli “trucchi” possano rendere la matematica estremamente intrigante e utilissima per mettere alla prova la nostra capacità di seguire ragionamenti logici di importanza ben più generale.
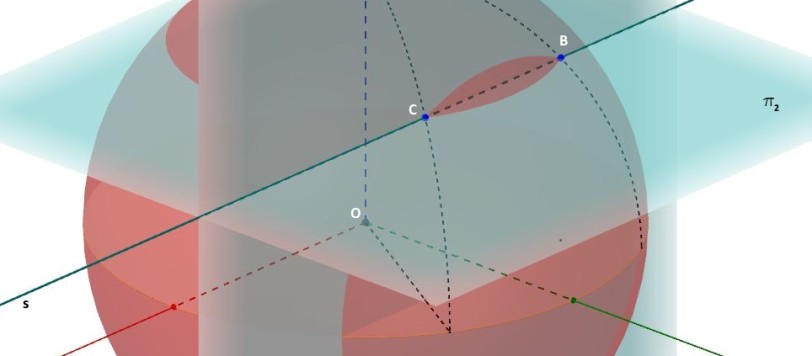
Dopo il primo articolo sulla geometria solida, pubblicato in due parti QUI e QUI nelle scorse settimane, eccoci ora giunti a questa appendice. In essa, mettendo in pratica i concetti di geometria solida sinora esposti, con particolare riferimento al piano, al fascio proprio di piani e alla sfera, dimostreremo che, dati due punti su una […]

Non troppo caldo né troppo freddo. Questa frase ci perseguita, soprattutto dopo l’articolo-riflessione di ieri sulla Relatività Generale e sui buchi neri galattici. Sembra quasi che ci abbiano sentito… ed ecco una nuova informazione, ancora troppo debole per essere accettata con entusiasmo, ma è la prima volta che osservazioni dirette sembrano confermare una teoria sulla formazione dei motori delle prime galassie, lasciata sempre un po’ in disparte.

L’inizio di questo articolo sembrerebbe solo una provocazione. Tuttavia, spero sia utile per capire il ruolo dei vari oggetti del grande Teatro del Cosmo, dove tutto è utile e dove tutto segue le regole migliori per mantenere armoniosa una struttura che possiamo considerare infinita sia verso il macro che verso il microcosmo. La provocazione finisce, ovviamente, con un sentimento di ammirazione e di gioia immensa.

Nel 1948, intuendo la possibilità di modificare i missili militari V2 (quelli che, lanciati dal Terzo Reich durante la Seconda Guerra Mondiale, avevano mietuto moltissime vittime in varie città europee), l’Unione Sovietica diede inizio all’avventura dell’uomo nello spazio. Dall'altra parte del mondo, l’inventore di quei missili, il tedesco Wernher Von Braun, divenne l’artefice dei maggiori successi spaziali americani, primo su tutti lo sbarco sulla Luna. Dopo l’euforia e i colossali investimenti degli anni ’60 del secolo scorso, i programmi spaziali subirono un rallentamento, ma negli ultimi anni ha ripreso vigore il progetto della missione umana su Marte che, ci dicono, potrebbe avvenire entro una ventina d’anni. E dopo? Cosa accadrà se e quando l’uomo avrà sviluppato la tecnologia per affrontare viaggi interstellari? Il nostro Vin-Census ha provato ad immaginarne uno con un epilogo che nessuno si aspetta! O forse qualcuno lo stava aspettando?!

Questa news, decisamente interessante dato che c’è di mezzo ALMA (una sicurezza), sembrerebbe quasi un colloquio tra un medico di famiglia e un oggetto tra i più misteriosi dell’Universo, un buco nero molto riservato e poco esibizionista.
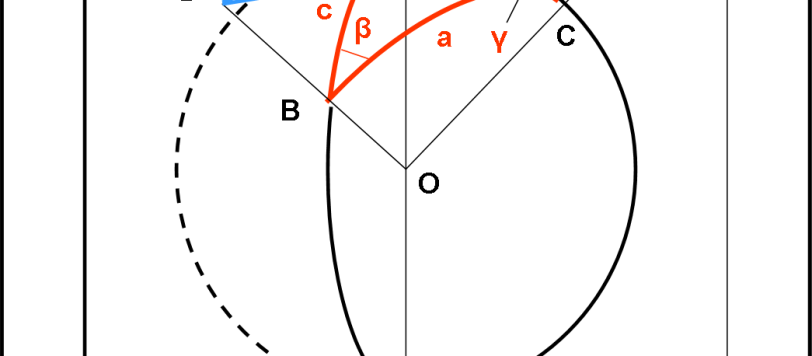
Definito il triangolo sferico, sia intrinsecamente che estrinsecamente, non ci resta che determinare alcune formule fondamentali che leghino tra loro i lati e gli angoli. Esse vengono proprio chiamate le tre formule fondamentali della trigonometria sferica.

L'insieme di Cantor, anche detto polvere di Cantor, ci servirà per provare che la cardinalità dell'insieme delle parti è minore o uguale a quella del continuo (R).L'insieme è anche un primo approccio al mondo fantastico dei frattali; nella figura una versione tridimensionale dell'insieme di Cantor.
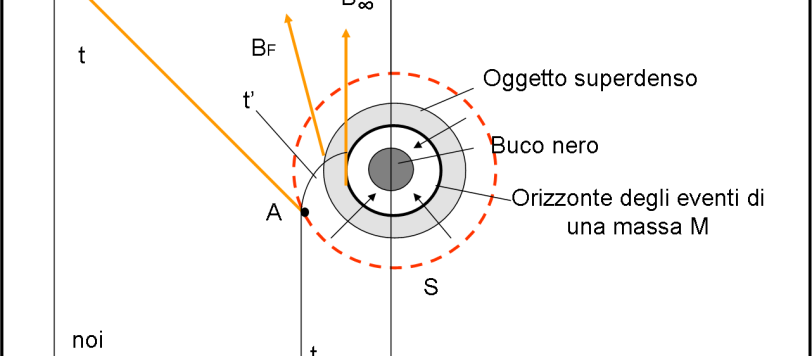
Scoprire un buco nero accompagnato da una sorellina che si prende cura di lui potrebbe essere relativamente facile. L'impresa sarebbe ben più ardua, e apparentemente impossibile, se il buco nero vivesse da solo. Tuttavia, una ricerca, soltanto teorica per adesso, potrebbe indicare la via da seguire.
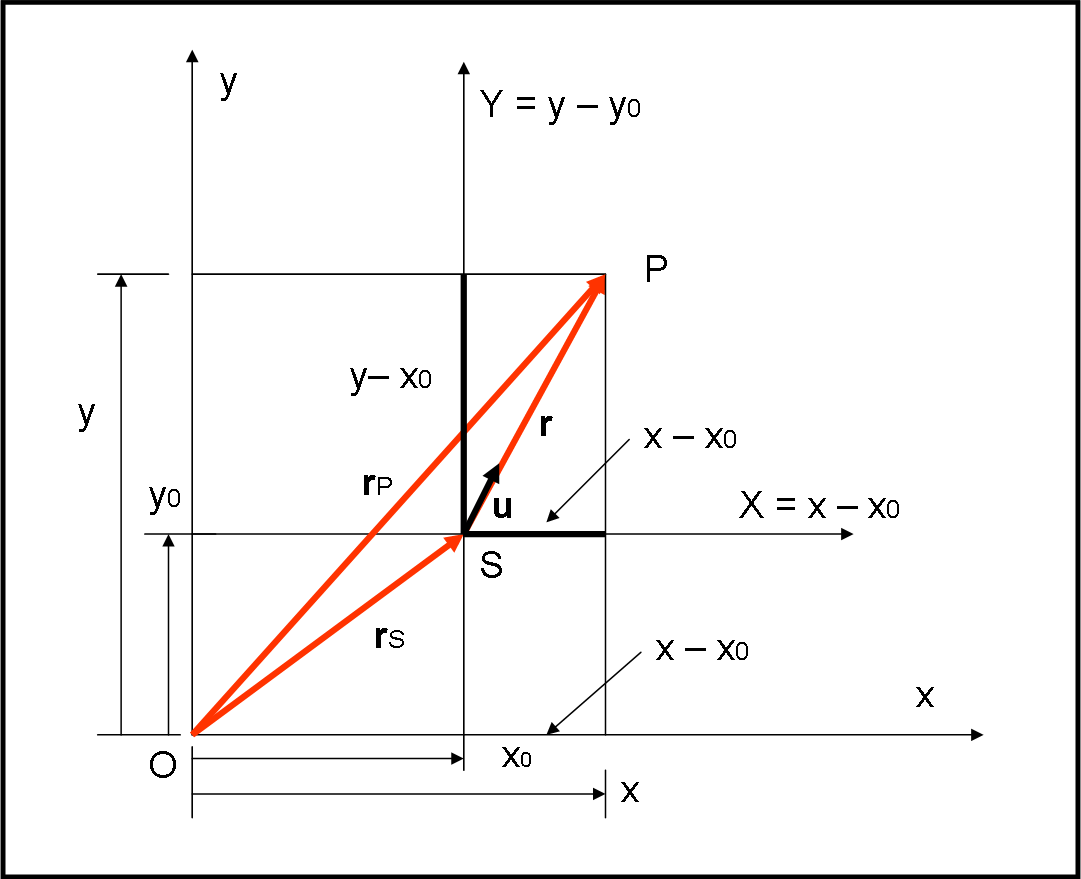
Attraverso tanti calcoli analitici (di media difficoltà, anche se un po' noiosi) si possono ricavare le tre leggi di Keplero partendo dalla legge di gravitazione universale di Newton. Vi è un solo punto critico relativo alla derivazione della traiettoria del corpo orbitante: un'equazione differenziale che comporta il calcolo di un integrale non banale (per noi almeno). Solo in questo caso accettiamo di prendere un risultato per buono... Per dirla in altre parole, risolviamo un problema fondamentale di Meccanica Celeste: il problema dei due corpi.
- 1
- 2

