Il presente articolo è stato inserito nella sezione d'archivio  "Quattro passi nella storia della Scienza" e in "Antichi Greci, che passione!"

Una volta mandati a riposare Astericcio & co., emozionatissimi per aver parlato a lungo con alcuni dei più grandi pensatori dell'antica Grecia (QUI), il loro e nostro nuovo amico Curiosità ha voluto scrivere questa appendice per permetterci di approfondire la conoscenza di uno dei periodi più luminosi nella storia dell'intelletto umano. Tutto ciò non vuole (e non potrebbe) essere una trattazione esaustiva, ma solo stimolare interesse, stupore e... curiosità!

 

L’Astronomia, o meglio l’Astrologia, nasce con l’uomo. Fin dalla preistoria l’osservazione del cielo e dei suoi oggetti gioca un ruolo fondamentale sia nella religione che nelle pratiche di tutti i giorni. Resta famoso il dipinto ritrovato nella grotta di Lascaux, dove circa 16500 anni fa sono stati ritratti un Toro (simbolo dell’omonima costellazione) e, sopra di esso, un gruppetto di stelle perfettamente simili alle Pleiadi

Sia presso gli egiziani che, soprattutto, presso i babilonesi si era arrivati a descrivere i fenomeni celesti più appariscenti con grande precisione. Proprio a questi ultimi si deve la misurazione sessagesimale e lo studio accurato dei moti solari. Tuttavia è solo con la civiltà greca che nasce veramente l’astronomia come scienza.
Tuttavia, prima di iniziare un sintetico resoconto delle principali conquiste dell’antica astronomia greca, è bene spiegare la differenza tra astronomia ed astrologia, che molti confondono e le cui origini, che si perdono nella notte dei tempi, forse pochi conoscono.
In realtà l’astronomia è figlia dell’astrologia, nel senso che è una sua derivazione di tipo intellettuale, razionale e conoscitivo e, per comprenderne le origini, è necessario analizzare la fase di passaggio da uomo nomade cacciatore a uomo stanziale agricoltore, durante la quale gioca un ruolo fondamentale l’intuizione prima, e l’accettazione completa dopo, del concetto di collegamento stretto tra ciclo stagionale agricolo e ciclo annuale del Sole.
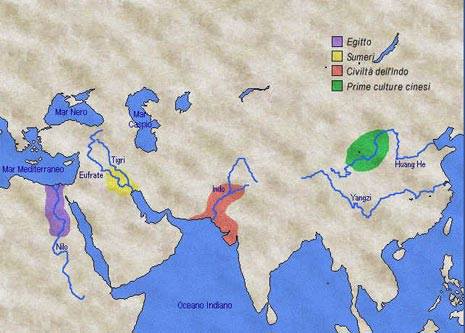
Il salto di qualità avvenne circa 6.000 anni fa, quando si formarono i primi veri stanziamenti urbani. Essi erano concentrati lungo i corsi di grandi fiumi (Tigri-Eufrate, Indo, Nilo, Huang He o Fiume Giallo), dove si verificò quella che può essere considerata la più grande conquista dell’umanità di tutti i tempi: la nascita dello stato organizzato. Non tutti facevano tutto, ma i compiti venivano sapientemente separati.
Proprio in questi agglomerati urbani, in cui la minore precarietà delle condizioni di vita donava il tempo di usare il proprio cervello anche per osservare e pensare, si cominciò ad alzare gli occhi al cielo con spirito “intellettuale”.
Non è difficile, quindi, comprendere che in questa fase di sviluppo ingenuo e primordiale, l’associazione della nozione astronomica di ciclo solare annuo all’influenza che esso esercitava sull’attività agricola, abbia determinato un naturale atteggiamento di rispetto sacrale per il “cielo”: esso non solo elargiva spontaneamente notevoli benefici, ma evidenziava una perfetta corrispondenza tra molti dei suoi fenomeni ed altrettante determinate conseguenze che si riversavano sulla Terra e che divenivano in tal modo perfettamente prevedibili. L’ovvia e naturale estensione, anche solo immaginaria, di questa corrispondenza ad altri aspetti della vita terrena, diede origine all’astrologia.

 

Per molto tempo rimase questo l’unico motivo di osservazione del cielo. Bisognava conoscere, seguire, studiare i fenomeni celesti che potevano avere una ricaduta sulla vita umana, per poterli prevedere correttamente e sfruttare al meglio. Ed era altrettanto importante che chi avesse particolare abilità nel fare ciò, fosse adeguatamente ricambiato dai potenti. Ovviamente la furbizia dell’essere umano era già sviluppata e molte interpretazioni degli “studiosi” erano mere invenzioni atte a propiziarsi i favori dei dispensatori di fama e ricchezza. Ma la mente umana cresceva comunque e con lei la consapevolezza di occupare un posto ben determinato nell’universo.
Passarono i secoli, si alternarono le civiltà, finché, circa 2.500 anni fa, principalmente presso i Greci, cominciò a nascere la voglia di conoscere e descrivere quello che avveniva nel cielo, senza nessuna contropartita pratica. Stava nascendo la ricerca scientifica che, tra errori enormi e pressioni religiose ed idealiste pressanti, cercava di collocare ogni cosa al suo giusto posto. Momenti di rara e forse mai più raggiunta genialità si succedevano a ricadute nella superstizione e nell’ingenuità. Ed il tutto avveniva quasi sempre con strumentazioni di una semplicità e di una imprecisione disarmanti. Ma le idee erano spesso solide e brillanti e lasciarono per sempre il loro segno fino alla nascita della scienza moderna, in cui Galileo Galilei ebbe un ruolo fondamentale. L’astronomia scientifica aveva ormai preso la sua strada ben chiara e precisa, lasciando all’astrologia il compito di imbonire i potenti ed i creduloni. Purtroppo né lo scorrere del tempo, né le evidenze scientifiche, sono ancora riusciti a sconfiggere il bisogno di credere nei sogni e nelle illusioni che essa elargisce facilmente e rimane ancora radicata come un vero atto di fede incrollabile. Talmente incrollabile che resiste anche al tragicomico inserimento di un tredicesimo segno zodiacale, reso “necessario” dal voler tener conto della variazione dell’inclinazione dell’asse terrestre (precessione degli equinozi), che ha come ovvia conseguenza quella di fare cambiare segno zodiacale a moltissime persone. Ma gli “esperti” non hanno problemi a spiegare a chi si è sempre sentito un Leone come mai ora debba riconoscersi in un Cancro!

Per meglio comprendere come la teoria geocentrica sia rimasta un atto di fede per secoli e secoli, bisogna tener presente che il modello della perfetta armonia era la base su cui si muoveva la dottrina portante dell’antica Grecia. Ed è proprio questa visione che portò alla costruzione stupefacente, accurata e geniale di Tolomeo che riuscì, con una complicata geometria, a spiegare quasi completamente i fenomeni osservabili, pur basandosi su un’idea di base completamente errata. Egli riuscì a mettere d’accordo la visione spirituale con una complessa ed acuta trattazione scientifica. Ne segue che molte delle grandi intuizioni astronomiche greche che citeremo nel seguito sono spesso singoli episodi “trasgressivi”: non ci fu mai una vera scuola alternativa in grado di sconvolgere le idee di base.
Sarebbe troppo lungo e complesso citare tutti i grandi pensatori e matematici (come venivano chiamati allora, l’astronomia era infatti un branca della matematica) che hanno portato qualche tassello fondamentale (spesso caduto poi nell’oblìo) alla comprensione del cielo stellato. Prenderemo in considerazione solo alcuni personaggi, che forse più di altri hanno modificato o chiarito fenomeni prima di allora incompresi. Tra errori ed imprecisioni, dovuti spesso alla scarsa tecnologia ed ai limiti degli strumenti di misura, assisteremo a qualcosa di molto simile a veri e propri capolavori “artistici” e non solo scientifici, talmente geniali sono state le intuizioni.
Spesso i personaggi sono avvolti nella nebbia dei secoli e sono poco chiare le loro opere ed i loro risultati. Magari quello che è attribuito ad uno è invece opera di un suo allievo o viceversa. Ma questo poco importa. Non è il valore del singolo personaggio la parte più importante, ma quello che in pochi secoli è stato estratto dalla mente umana, mai prima di allora così logica, intuitiva e precisa (e ciò varrà poi anche per molti secoli futuri).

L’inizio della scienza astronomica greca si fa risalire alla Scuola Ionica, quella di Talete, Anassimandro e Anassimene, siamo nel periodo che va dal 630 al 540 a.C. circa. Talete immaginò la Terra galleggiare sull’acqua. Sicuramente più stimolante è la versione di Anassimandro: fu lui forse il primo a dire che i corpi celesti eseguono percorsi circolari, ed ancora più geniale fu la sua intuizione che la Terra galleggiasse nello spazio senza bisogno di alcun sostegno.
Si dice che Anassimandro abbia introdotto in Grecia l’uso dello gnomone, apprendendolo probabilmente dai Babilonesi, strumento semplice (un’asta rigida), ma fondamentale per tutte le misure che si compiranno negli anni successivi.

La figura di Filolao di Crotone (470 a.C. – 390 a.C.), riveste grande importanza nella storia della cosmologia, infatti è ritenuto il primo ad aver tolto la Terra dalla posizione centrale del Cosmo

 

Parmenide di Elea, che visse all’incirca dal 515 a.C. al 460 a.C. fu probabilmente il primo ad affermare che la Terra fosse sferica ed occupasse il centro dell’universo. La tradizione lo considera anche il primo ad aver riconosciuto che Espero o Vespero (stella della sera) e Lucifero (stella del mattino) fossero lo stesso astro, Venere.

Ancora più fondamentale è stata la figura del matematico ed astronomo Enopide di Chio (circa 490-420 a.C.) che è stato probabilmente il primo a misurare l’angolo tra il piano dell’eclittica (il piano che contiene l’orbita della Terra) ed il piano dell’equatore terrestre, la cosiddetta obliquità. Si dice che Enopide abbia ottenuto il valore di 24°, che rappresenta una stupefacente approssimazione (il valore vero è di 23° 27’). Ancor più stupefacente se si considera che è stato ottenuto con un semplicissimo strumento usato con tanta intelligenza. Lo strumento in questione è lo gnomone, consistente in un’ asta rigida, dell’altezza di circa due metri, infissa nel terreno con la massima accuratezza possibile secondo la verticale. Esso permetteva di ricavare l’altezza meridiana del Sole (l’altezza del Sole sull’orizzonte al mezzogiorno locale). Il suo impiego richiedeva di prendere nota della lunghezza dell’ombra proiettata dallo strumento sulla linea meridiana nord – sud a mezzogiorno (tale istante coincide ovviamente con quello in cui la l’ombra è minima).
Va ricordato che prima dell’introduzione della trigonometria i Greci si arrangiavano con metodi grafici-euclidei.

 

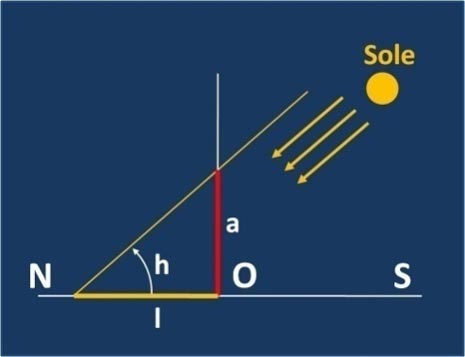
E’ quasi stupefacente pensare che con il solo gnomone Enopide ricavò sia il valore dell’obliquità dell’eclittica che quello della latitudine del luogo. La figura sottostante dimostra geometricamente che Enopide aveva proprio ragione!

 

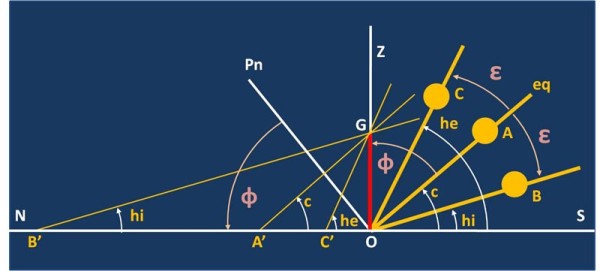
Anche se di carattere non strettamente “astronomico” non si può tacere l’intuizione fisica di Empedocle di Agrigento (492 a.C. – 430 a.C.), secondo cui la velocità della luce era finita, per cui impiegava un certo tempo a percorrere una certa distanza.

Democrito di Abdera (460 a.C. – 380 a.C.) è considerato invece il più autorevole rappresentante della scuola atomistica: immaginò l’essenza del mondo composta da particelle di materia più o meno piccole, non ulteriormente divisibili: gli atomi. Secondo Democrito, tutto ciò che esisteva era prodotto dalle varie combinazioni degli atomi. Essi erano le uniche realtà durevoli, mentre l’esistenza del vuoto era condizione indispensabile al loro movimento.

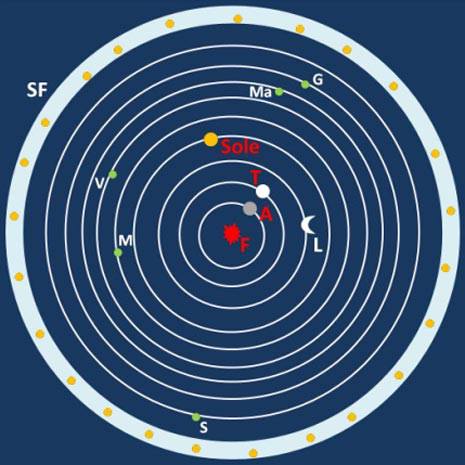
Eraclide Pontico (385 a.C. – 322 a.C.) fu forse il primo a sostenere la teoria dei moti di Mercurio e Venere intorno al Sole, pur lasciando a quest’ultimo il suo moto intorno alla Terra, secondo lo schema della figura

 

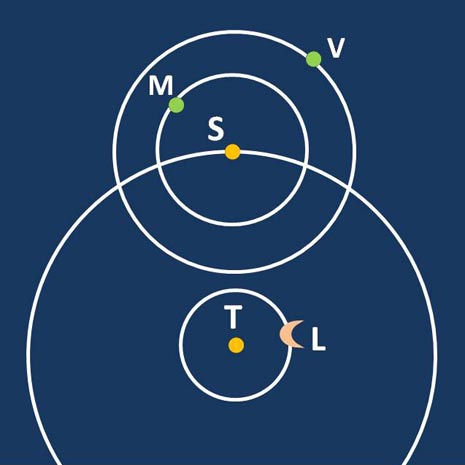
Veramente fondamentale è stata la figura di Aristarco di Samo (310 a.C – 230 a.C.). A lui è riconosciuto il merito di essere stato il primo aperto sostenitore del moto della Terra intorno al suo asse e del moto di essa attorno al Sole. A lui cioè è dovuta la prima formulazione dell’ipotesi eliocentrica. Dato che la Terra si muoveva intorno al Sole lungo un cerchio, Aristarco ipotizzò che “le stelle, essendo fisse, avrebbero dovuto mostrare un moto annuo apparente nel cielo, a causa della variazione della posizione della Terra rispetto a loro mentre compiva il suo moto intorno al Sole”. Questo movimento apparente avrebbe dovuto essere un’ellisse (a causa della direzione della stella rispetto al piano orbitale della Terra) ed è proprio quello che viene oggi chiamato parallasse annua. Dato che questo movimento non si osservava, egli concluse che le stelle fisse si dovevano trovare a distanze enormemente maggiori del diametro dell’orbita terrestre. In realtà il movimento c’è, ma è troppo piccolo perché potesse essere misurato con gli strumenti dell’epoca, infatti è stato possibile rilevarlo solo nel 1838.

 

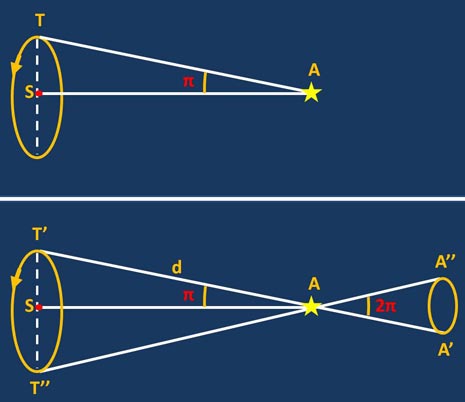
Aristarco fu anche il primo ad affrontare il problema di misurare geometricamente le distanze di Luna e Sole dalla Terra, nonché le dimensioni stesse dei due astri.

 

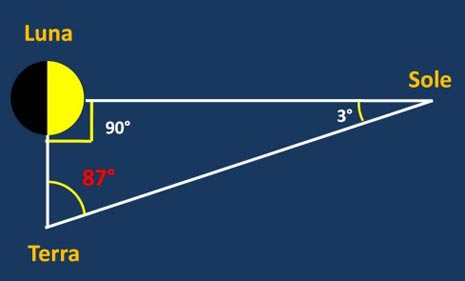
Lavorando con il metodo euclideo (non conoscendo ancora la trigonometria) Aristarco determinò che la distanza Terra-Sole era “da 18 a 20 volte la distanza Terra-Luna”. Ovviamente a quell’epoca la strumentazione di cui poteva disporre Aristarco era grossolanamente imprecisa, e sarebbe stato assolutamente impossibile per lui misurare l’effettivo angolo Sole-Terra-Luna che è invece di circa 89° 51’ (la distanza Terra-Sole, in effetti, è circa 390 volte quella tra la Terra e la Luna). Malgrado il risultato sia estremamente impreciso, resta indubbio il fatto che la strategia osservativa era perfettamente corretta e geniale.

Il ragionamento successivo di Aristarco derivò dal fatto che, nelle eclissi totali di Sole, questo viene coperto per intero dalla Luna. Da ciò si poteva dedurre che i loro diametri apparenti erano eguali. Ne derivava una figura come quella che segue, in cui entrambi i raggi apparenti sottendono lo stesso angolo.

 

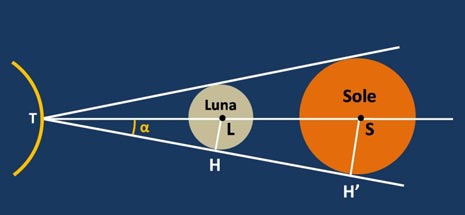
Altra figura luminosa è stata quella di Eratostene di Cirene (276 a.C. – 194 a.C.). Egli aveva avuto notizia (o, forse, lo aveva constatato direttamente) che a Siene (l’odierna Assuan), nell’Alto Egitto, il Sole era esattamente allo zenit il giorno del solstizio estivo. Ciò era provato dal fatto che a mezzodì di quel giorno, entro un raggio di circa mezzo miglio e per un attimo, il fondo di ogni pozzo appariva completamente illuminato dalla luce del Sole. Invece ad Alessandria d’Egitto, nello stesso giorno ed alla stessa ora, gli obelischi e le altre strutture verticali producevano un’ombra, seppure molto corta. Eratostene allora, con geniale intuizione, misurò mediante l’utilissimo gnomone, che ben conosciamo, la lunghezza dell’ombra a mezzogiorno del solstizio d’estate ad Alessandria e riuscì facilmente a calcolare l’angolo tra la direzione del Sole e quella della verticale del luogo (ossia quella dello gnomone), come riportato nella figura che segue

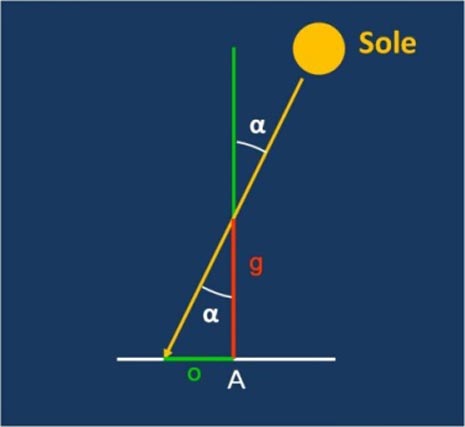
Aveva già mandato nel frattempo il suo servo a Siene a dorso di dromedario per misurare il più esattamente possibile la distanza tra le due città. A questo punto Eratostene fece una semplice proporzione e calcolò la misura della circonferenza terrestre come illustra la figura

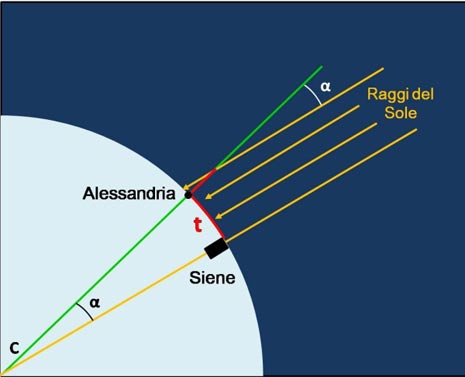
Notiamo che il ragionamento era valido soprattutto a seguito delle importanti assunzioni che i raggi solari potessero essere considerati paralleli tra loro, ossia che il Sole si trovasse a distanza enorme rispetto alla alla Terra, che questa fosse sferica e che Alessandria e Siene fossero sullo stesso meridiano (tutte ipotesi esatte, ma decisamente coraggiose). Eratostene misurò un angolo di 1/50 di circonferenza ed ottenne una distanza tra le due città di 5000 stadi. La semplice proporzione che deriva dalla figura precedente gli permise di calcolare una circonferenza di 250000 stadi, pari a 39375 km, contro gli effettivi 40000. Grande Eratostene ma perfetto come contachilometri anche il dromedario!

Malgrado si eseguissero misurazioni eccezionali e si avessero intuizioni geniali, va ricordato che il pensiero dominante, di tipo filosofico-religioso, seguiva le indicazioni di Platone e dei pitagorici che vedevano l’universo come una successione di sfere cristalline, quindi solide, che trasportavano in successione nei loro movimenti attorno alla Terra, naturalmente immobile al centro del cosmo, la Luna, il Sole, Mercurio, Venere, Marte, Giove, Saturno e da ultimo la sfera delle stelle fisse. Soprattutto erano assolutamente indiscutibili gli assiomi della circolarità dei moti di tutti gli astri (il cerchio era la figura geometrica che maggiormente racchiudeva i caratteri della perfezione) e della uniformità nel percorrerli. Ma, poiché l’osservazione del moto dei pianeti mostrava delle irregolarità (stazionamenti, moti retrogradi e apparenti variazioni di velocità), Platone esortava gli astronomi a escogitare rigorosi metodi matematici che avrebbero permesso di spiegarle, preservando gli assiomi di cui sopra.
Ricordiamo infatti che il moto apparente dei pianeti è piuttosto complesso, presentando traiettorie che formano “cappi” e che variano di velocità. Tutte cose che NON potevano essere spiegate con il semplice moto attorno alla Terra.

 

 

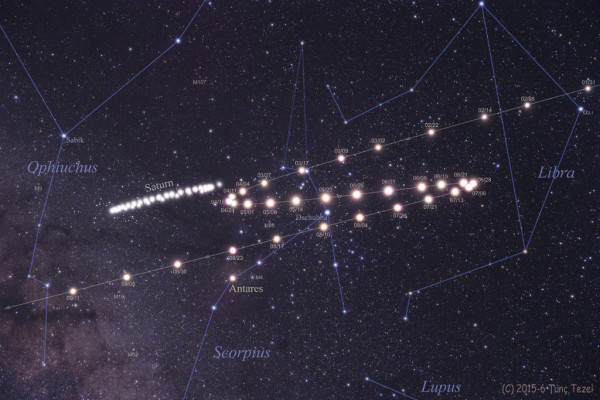
Partendo quindi da idee errate, la grande capacità razionale e matematica dei greci riuscì a trovare modelli che spiegassero le anomalie riscontrate, in modo da non collidere con i principi fondamentali. Una grande fatica inutile, se vogliamo, ma una prova straordinaria delle applicazioni geometriche e matematiche, che porteranno alla fine al meraviglioso, anche se completamente sbagliato, modello tolemaico.

Apolonnio di Perga fu forse il primo a dare una versione scientifica alle incongruenze che apparivano nel modello pitagorico e di Platone. Egli visse dal 262 al 190 a.C. circa ed era noto come “il grande geometra”. Ebbe una grande influenza sullo sviluppo della matematica, specialmente per la sua opera più famosa, le coniche, in cui introdusse termini matematici quali ellisse, parabola, iperbole, che continuano ad essere usati.
Per spiegare le anomalie nel moto dei pianeti e del Sole, Apollonio introdusse in modo rigorosamente matematico le costruzioni geometriche degli epicicli e degli ex-centri.

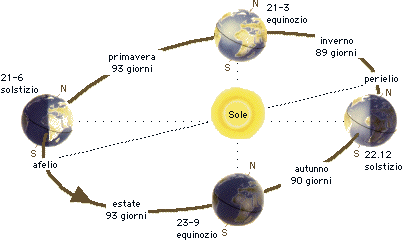
Prima di procedere alla loro descrizione dobbiamo partire dall’epoca, invero molto remota, in cui si ebbe la cognizione dell’anomalia solare, che per gli Antichi era riscontrabile, in pratica, nelle differenti durate delle stagioni:

Intorno al 130 a.C. fu Ipparco ad eseguire la migliore determinazione di durata dell’anno e delle singole stagioni ma, ancor prima di lui, sembra che i Greci avessero stabilito che le durate di esse si potevano spiegare con uno schema come quello illustrato nella figura che segue

Apollonio, da grande matematico, introdusse una costruzione geometrica particolare, dimostrando l’equivalenza con quella della figura precedente, continuando ad obbedire completamente ai canoni risalenti alla scuola pitagorica e consacrati dalla fisica aristotelica, che dovevano essere conservati. Questi canoni astronomici, già accennati precedentemente nella loro espressione esteriore, possedevano una intima valenza trascendente che andava ben oltre la loro semplice apparenza geometrica: erano i “fenomeni da salvare”, cioè: (1) l’orbita solare è un cerchio, (2) la Terra, essendo centro del cosmo, deve essere centro di questo cerchio e (3) la velocità del Sole su questo cerchio deve essere costante.

Vediamo allora in dettaglio come sia riuscita in questa dimostrazione:

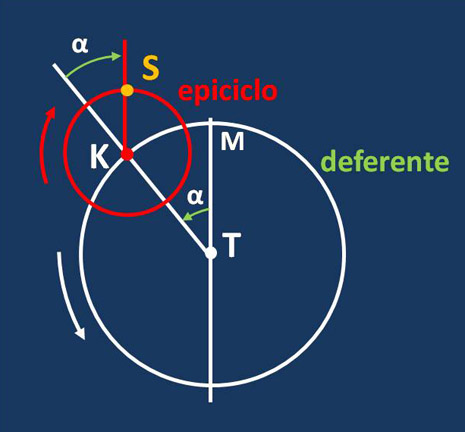
Secondo Apollonio, dunque, il Sole circola con periodo di un anno, con moto uniforme e in senso orario su un cerchio, detto epiciclo, il cui centro circola a sua volta, in senso antiorario e con lo stesso periodo di un anno, su un altro cerchio, detto deferente, centrato nel centro della Terra. Vengono così conservati i principi base: cerchi perfetti, moti uniformi e Terra al centro.

In questa combinazione di movimenti il raggio dell’epiciclo del Sole si mantiene sempre orientato parallelamente ad una certa direzione. Ciò però è equivalente a dire che il Sole descrive un cerchio di raggio eguale al raggio del deferente, ma il cui centro è spostato fuori del centro della Terra (ex-centro) di una quantità pari al raggio dell’epiciclo solare. In definitiva quindi è come se il Sole circolasse su un cerchio (uguale al deferente) ma avente centro diverso dalla Terra. L’equivalenza è perfettamente dimostrata, come illustrato nella figura che segue.

Veramente un’operazione matematica e geometrica geniale, anche se del tutto… sbagliata. In modo analogo, anche se più complicato, Apollonio spiegava il moto dei pianeti interni ed esterni, dando ragione di molte anomalie. In realtà però molte cose non tornavano esattamente. Resta, comunque, il fatto che la piattaforma matematica di Apollonio sarà quella che consentirà a Tolomeo di conseguire i suoi notevoli progressi astronomici. E’ quindi del tutto lecito accordare ad Apollonio un posto di assoluto rilievo.

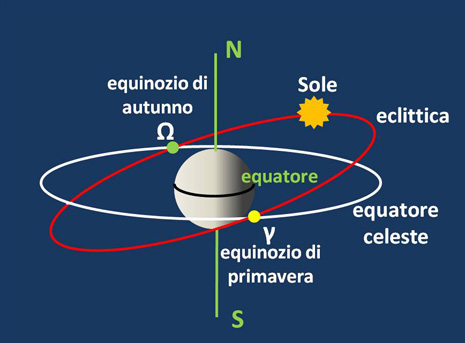
Altra figura fondamentale è stata quella di Ipparco di Nicea (190 a.C – 120 a.C.). La maggior parte delle informazioni che abbiamo su di lui ci sono giunte attraverso le opere di Tolomeo. Alcuni hanno sostenuto perfino che l’invenzione della trigonometria si debba proprio a lui. Di certo si deve a lui il calcolo esatto della lunghezza dell’anno tropico, ossia del tempo impiegato dal Sole per tornare nella stessa posizione, vista dalla Terra, lungo l’eclittica, e che ha come punto zero il punto d’Ariete (punto γ) o equinozio di primavera. Questo è il punto che introduce la primavera astronomica ed è uno dei due (l’altro è il punto della Bilancia (punto Ω) o equinozio d’autunno) in cui l’equatore celeste interseca l’eclittica, come è illustrato nella figura seguente:

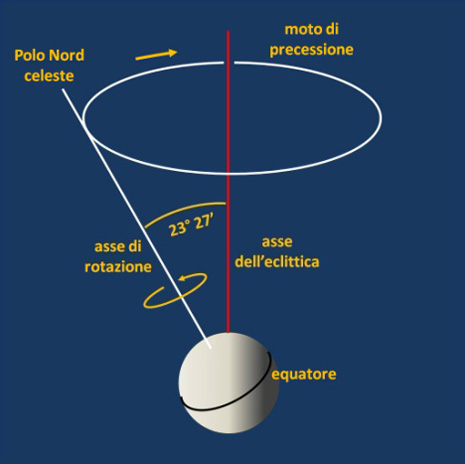
Ipparco calcolò l’anno con una precisione di circa 6 minuti, ma soprattutto scoprì la precessione degli equinozi attribuendole il valore annuo straordinariamente preciso di 45 secondi d’arco. La precessione degli equinozi altro non è che il lento movimento dell’asse terrestre attorno all’asse dell’eclittica, che si compie in 25800 anni circa. A causa di ciò gli equinozi (d’autunno e di primavera) si spostano costantemente lungo l’eclittica di una valore annuo che oggi sappiamo essere di 50,26 secondi d’arco. Eccezionale quindi non solo la precisione ottenuta da Ipparco, ma il fatto stesso di avere scoperta e correttamente interpretata questa lenta ed impercettibile variazione. La precessione fa si che al giorno d’oggi la stella più vicina al polo Nord celeste sia la stella polare, mentre 3000 anni prima di Cristo era la debole Thuban e tra 12000 anni sarà la brillantissima Vega.

Famoso è anche il suo catalogo di stelle che conteneva circa 850 voci. Egli probabilmente iniziò la catalogazione avendo il sospetto che le stelle “fisse” potessero avere dei moti relativi. Plinio, nella sua Storia naturale, dice inoltre che grande importanza ebbe per Ipparco l’apparizione in cielo di una stella mai vista fino a quel momento, una nova stella (oggi ancora chiamate novae, sono esplosioni violentissime di stelle). Da ciò l’indagine del grande astronomo per appurare se le stelle nascono e muoiono, se variano di luminosità, e se si muovono le une rispetto alle altre, ecc… Ipparco fornisce un ottimo esempio di vero scienziato che, puntando alla ricerca della verità, non si cura di staccarsi dai dogmi aristotelici e platonici, uno dei quali riguardava appunto la inviolabilità della perfezione dei cieli.

Ipparco scoprì la precessione proprio confrontando le sue misure di longitudine di stelle con quelle precedenti. Trovò che tutte differivano di circa due gradi. Le latitudini celesti, invece, erano rimaste praticamente invariate. Si poneva ora il problema di stabilire se era l’intera sfera recante le stelle fisse ad aver ruotato verso est o se erano stati i punti degli equinozi ad aver ruotato verso ovest. Dopo qualche indecisione iniziale, Ipparco accettò la conclusione del moto dei punti equinoziali.

Claudio Tolomeo, il cui modello dell’universo sarà ritenuto valido fino alla rivoluzione copernicana (oltre quattordici secoli dopo, ma solo dopo ulteriori tre secoli si smise finalmente di insegnarlo), vive tra il 90 ed il 170 dopo Cristo ad Alessandria d’Egitto. La sua opera fondamentale è l’Almagesto, nome tratto dalla traduzione datagli dagli arabi, “al-majisti” (il grandissimo). Con essa Tolomeo si proponeva di fornire un compendio di nozioni astronomiche atte a spiegare il sistema cosmologico in tutte le sue espressioni. Partendo dai modelli matematici degli epicicli e degli ex-centri, come quello di Apollonio visto precedentemente, produsse, quale risultato finale, una procedura matematica predittiva delle posizioni di ciascun pianeta.
Nel sistema tolemaico il deferente è però eccentrico rispetto alla Terra ed il moto del centro dell’epiciclo lungo il deferente è uniforme rispetto ad un punto (equante) simmetrico della Terra rispetto al centro del deferente stesso. Insomma un’ulteriore complicazione pur di descrivere al meglio i fenomeni osservati.

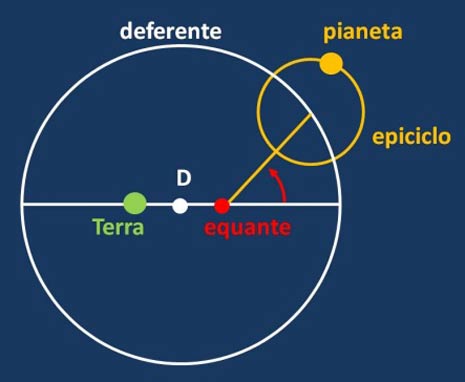
Malgrado sia universalmente conosciuto come sistema geocentrico, la Terra comincia a perdere il proprio ruolo centrale nell’universo, mentre il Sole acquista un ruolo essenziale nel moto di tutti i pianeti: infatti il periodo del moto lungo l’epiciclo dei pianeti esterni (Marte, Giove e Saturno) e quello dell’epiciclo lungo il deferente dei pianeti interni (Mercurio e Venere) coincide con quello del moto apparente del Sole (un anno). Alla Terra rimane però sempre la prerogativa di restare immobile. In realtà solo questa radicata convinzione può aver impedito a Tolomeo ed ai suoi seguaci di accorgersi che tutta la sua complicata costruzione sarebbe crollata e che tutti i movimenti apparenti dei pianeti potevano essere spiegati più semplicemente attribuendo tale periodo di un anno al moto di rivoluzione della Terra intorno al Sole.

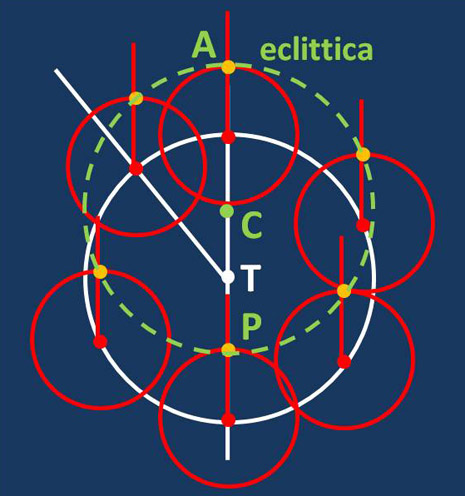
Una trattazione grafica accurata del complesso e sofisticato modello tolemaico sarebbe sicuramente di difficile e faticosa comprensione, comunque le figure che seguono ne danno una visione d’insieme, anche se molto schematizzata e semplificata, in quanto presentano l’imperfezione di non mostrare l’eccentricità dei cerchi deferenti. Mantengono però uno dei principi cosmologici propri della teoria tolemaica: nell’universo non si devono avere spazi vuoti, o meglio, spazi inutilizzati: ogni epiciclo deve essere tangente all’epiciclo successivo.

 

 

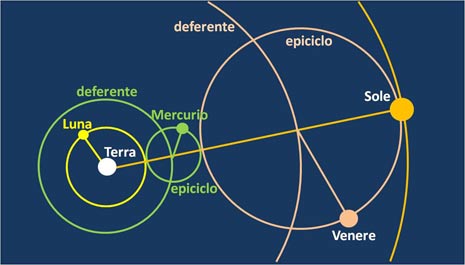
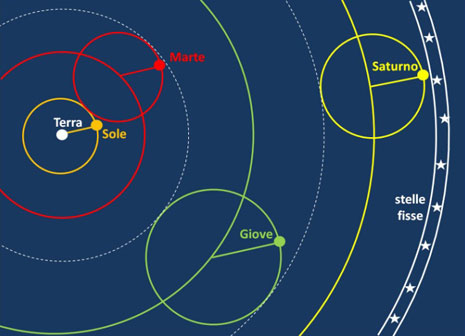
Liberamente tratto da "L'occhio infinito di Galileo" di Domenico Licchelli e Vincenzo Zappalà, di cui abbiamo parlato anche QUI

I super-curiosoni troveranno QUI una rassegna di articoli per continuare a meravigliarsi di fronte alle capacità e potenzialità di questi pensatori

Sarà vero che è stato Colombo a scoprire l'America? Dipende da cosa s'intende per "scoprire"... sentiamo cos'ha da raccontarci l'inossidabile coppia Curiuss-Gualtiero circa le capacità deduttive degli antichi greci!

Tutti i racconti di Ciccio e Astericcio sono disponibili nella rubrica ad essi dedicata