Non si sa bene il significato del nome “stomachion”, ma sicuramente è stato studiato a fondo, se non addirittura creato, da Archimede. Questo non è un quiz, ma un gioco che si ricollega a una versione più semplice di origine cinese. Buon divertimento!

Il significato della parola greca sembrerebbe riportare a “irritazione”, come se fosse quello il sentimento che si dovrebbe avere di fronte al gioco che si deve impostare. Tuttavia, la parola potrebbe avere origine da “ostomachion” , ossia “battaglia degli ossi”, dato che in origine i vari pezzi venivano costruiti utilizzando ossicini, adeguatamente sagomati.

Sicuramente, Archimede, vi studiò sopra a lungo ed è probabile che sia stato proprio lui a inventarlo.

Iniziamo a costruirlo, partendo da un rettangolo che ha un lato doppio dell’altro, ma potrebbe essere usato qualsiasi parallelogramma. Chiamiamolo ABCD e utilizziamo la Fig. 1 per seguire le fasi costruttive.

Consideriamo i punti di mezzo dei lati lunghi AD e BC e indichiamoli con F ed E. Tracciamo il segmento EF che divide il rettangolo in due quadrati.

Disegniamo le diagonali AC, BF e FC. Indichiamo con L e R i punti d’intersezione della diagonale AC con la diagonale BF e con il segmento EF, rispettivamente.

Consideriamo il punto di mezzo G  della linea BE e da lui tracciamo una linea parallela al lato AB, che incontra la diagonale BF nel punto H. Congiungiamo, inoltre, G con il punto A, fermandoci in K, dove si incontra la diagonale BF.

Uniamo il vertice B con il punto di mezzo M di AL. A questo punto, abbiamo diviso il primo quadrato (o parallelogramma che sia) in 7 parti.

Siano, adesso, N e O i punti di mezzo dei segmenti CD e FC, rispettivamente. Tracciamo le linee ON e OE. Indichiamo il punto Q, intersezione di OE con la diagonale AC.

Sia, infine, P il punto intersezione di BO con  il lato CD. Tracciamo il segmento OP.

Anche il secondo quadrato (parallelogramma) è stato diviso in 7 parti.

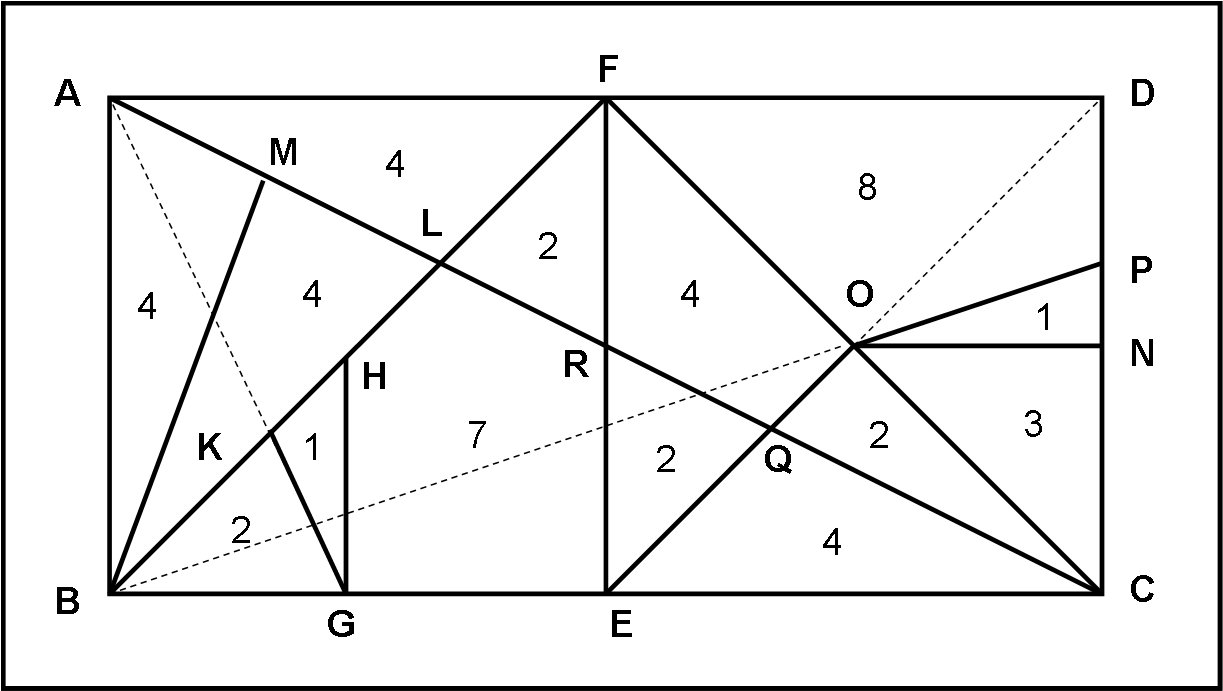
In totale abbiamo ottenuto 14 poligoni (11 triangoli, 2 quadrilateri e un pentagono)

E’ importante sapere che l’area di ogni poligono può essere espressa in quarantottesimi dell’area del rettangolo (parallelogramma) iniziale. In’altre parole, se poniamo l’area totale uguale a 48, ognuno dei 14 poligoni può essere espresso come frazione di numeri interi, il cui denominatore è sempre 48. I numeri all’interno dei vari “pezzi” indicano proprio il numeratore di queste frazioni, ossia quanti quarantottesimi dell’area totale rappresentano le loro aree.

Come conferma della libertà di scelta della figura di partenza, ricostruiamo i 14 pezzi, utilizzando un quadrato iniziale. La Fig. 2 mostra che il procedimento è esattamente lo stesso e che i rapporti tra i poligoni restano sempre uguali.

 

Per chi volesse costruirsi direttamente i 14 pezzi del gioco consigliamo di usare un foglio a quadretti. Le misure devono essere molto precise.

Da un punto di vista puramente matematico si può verificare la moltitudine di poligoni regolari che possono essere costruiti con i 14 pezzi (si parla di migliaia e migliaia). Ne vediamo qualche esempio in Fig. 3.

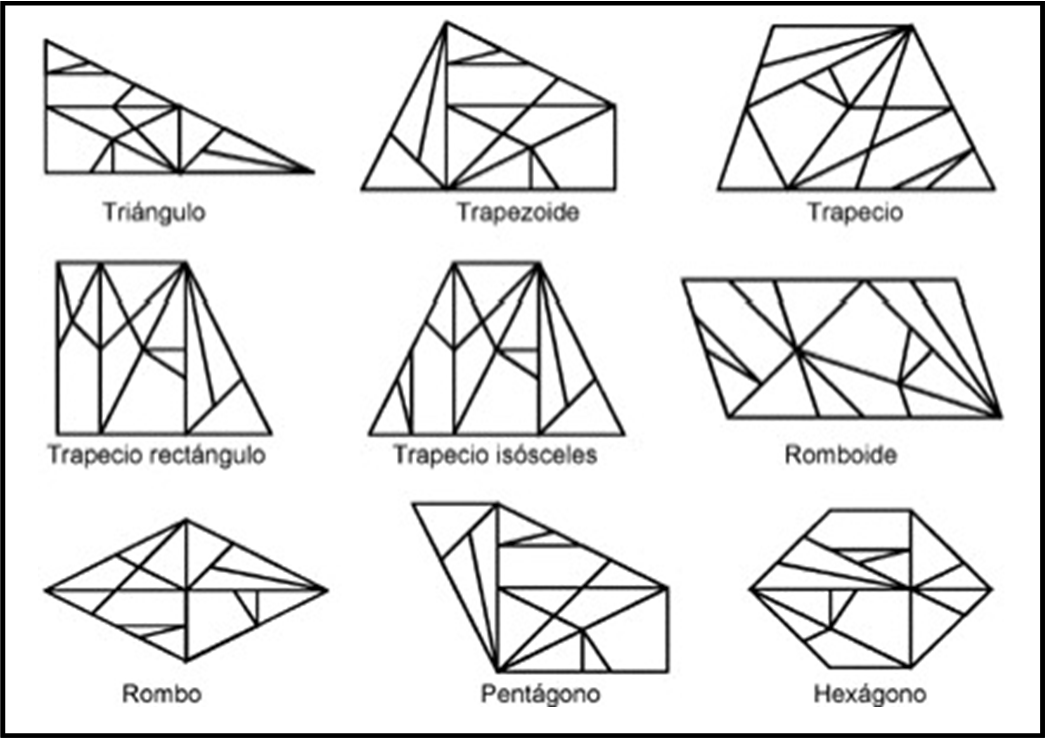
Tuttavia, le straordinarie possibilità offerte dal gioco si notano molto meglio nella Fig.  4, dove non è difficile riconoscere che tipi di animali si sono costruiti. I  risultati sono facili da ottenere, dato che sono riportati i vari pezzi.

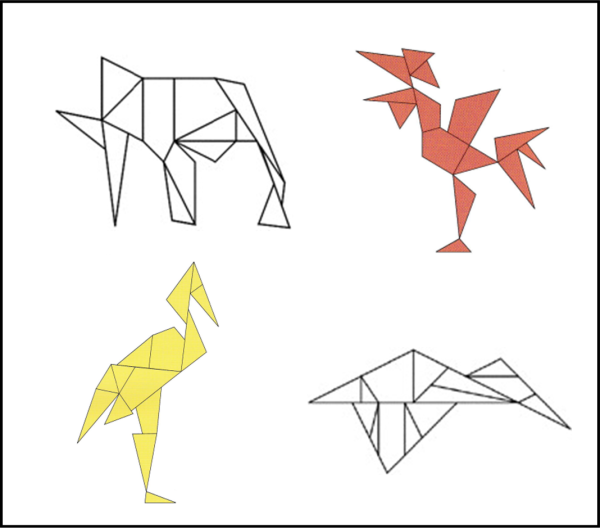
Molto più difficile è ripetere le immagini presentate nella Fig. 5, dove si vede solo il profilo finale.

La cosa migliore, però, è lasciare libera la propria fantasia e inventarsi figure sempre più strane e accurate. Le possibilità sono praticamente infinite…

Attenzione, comunque, alle regole del gioco:

1) Devono essere utilizzati tutti e 14 i pezzi

2) Non devono esserci sovrapposizioni tra i pezzi

Forza datevi da fare e pubblicheremo i più belli e fantasiosi, ricordando che stiamo facendo un viaggio nel passato, in cui potete immaginarvi di essere a fianco di Archimede, gareggiando con lui!

Chi volesse cominciare con qualcosa di più semplice (ma sempre molto stimolante, ve lo assicuro), può dedicarsi a un gioco simile di origine cinese, il tangram, che viene tradotto come “le sette pietre della saggezza”. Esso si costruisce partendo da un quadrato che viene ritagliato in 7 pezzi, come mostrato in Fig. 6, dove i vari punti rappresentano quasi sempre i punti di mezzo dei vari segmenti.

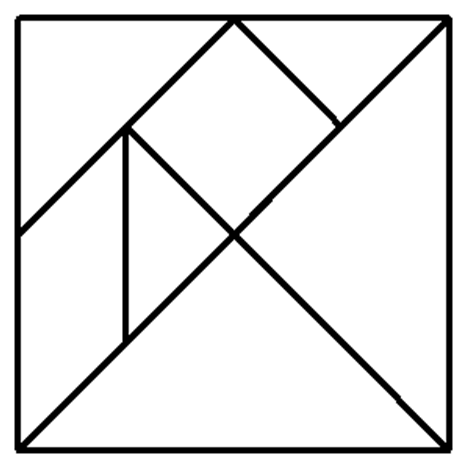
Attendo moltissime risposte e moltissime figure imprevedibili…

N.B.: Un consiglio per le mamme e i papà (ma non solo). Prendete un foglio di compensato e disegnategli sopra il quadrato o il rettangolo, segnando molto bene le righe dei vari pezzi. Con un righello e un taglierino è facile ricavare i 14 o 7 pezzi, che non si rovinino troppo in fretta. Un gioco decisamente più divertente e utile di quelli che propinano i programmini pappa-pronta dei cellulari o come diavolo si chiamano adesso!