QUIZ geometrico e culinario: come fare due fette uguali, ma molto strane **
Un semplice quiz geometrico in cui bisogna dividere una torta quadrata, in due fette con la stessa area, ma con una forma piuttosto strana. I grandi “chef” fanno tutto e di più…
La nostra torta ha una forma quadrata ed è molto invitante… Lo chef deve ricavarne due fette di area uguale, ma vuole dare la massima libertà alla sua fantasia. Studia la situazione e poi trova una soluzione un po’ bizzarra, ma che serve sicuramente a dargli una notevole fama, indipendentemente dal sapore della torta…
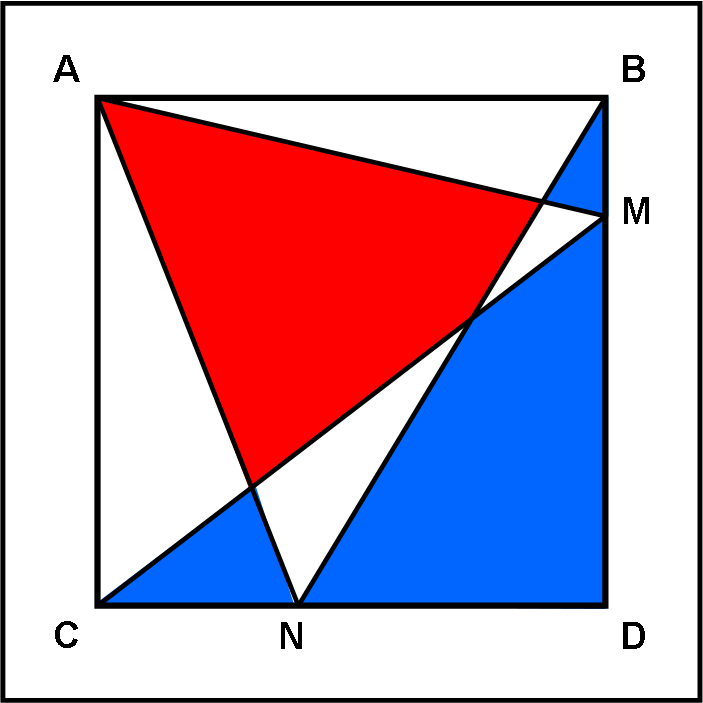
Il quadrato è ABCD. La domanda è: “Come devono essere scelti i punti M e N affinché la fetta rossa si uguale alla fetta azzurra?”
La soluzione QUI






18 commenti
Altro che buon appetito... così la torta mi va di traverso!!
Sai che c'è? Me la mangio tutta così elimino il problema alla radice!
intendendo per fetta azzurra l'unione dei tre pezzi azzurri visibili nell'immagine, opportunamente composti, oppure solo il quadrilatero NDMX (con X punto di intersezione di CM con BN ?
caro Arturo,
la fetta azzurra è tutta la parte azzurra, anche se sembra divisa in tre pezzi ... lo chef riesce a presentarla tutta insieme con grande maestria... :-)
caro Scherzy... si vece che su Papalla non esistono i grandi chef,,,,
Scusa, Enzo, per uguali intendi che devono avere la stessa area o devono anche essere congruenti?
Sì, hai ragione Dany... sono stato troppo frettoloso. Intendo dire che abbiano la stessa area, dato che le porzioni devono essere uguali. Dimentico sempre qualcosetta, che do per scontato... Uffa!
Ho cambiato adeguatamente il testo...
Grazie!!!!
Ecco la soluzione che mia figlia Valentina ha elaborato, lavorando con Geogebra.
L'idea è che i punti M e N possano trovarsi in qualunque posizione purché sia CN=BM (e di conseguenza ND=MD
Lasciando perdere una dimostrazione di carattere generale, abbiamo verificato due casi:
1° caso
area rossa = AGHI = 14,35 area azzurra = BGE+IFD+EHFC = 0,37+0,37+13,61 = 14,35
2° caso
area rossa = JPQR = 11,78 area azzurra = KPN+MOR+NQOL = 1,09+1,09+9,6 = 11,78
cara Dany (e Vale...),
sicuramente avete trovato due fette uguali come area, ma la definizione dei punti M e N non è quella esatta... o almeno non è quella più generale possibile.
Infatti, CN può essere anche diverso da BM. Cioè, qualunque posizione assumano i punti N ed M, purché rispettivamente sui lati CD e BD, l'area della parte rossa risulterà uguale alla somma delle aree azzurre.
per favore... una spiegazione più esauriente...

Una dimostrazione che mi viene in mente fa uso della geometria analitica nel piano.
Con riferimento alla seguente figura:
facciamo coincidere il vertice C con l'origine degli assi cartesiani e indichiamo con l il lato del quadrato ABCD, con a l'ascissa del punto N (di ordinata zero) e con b l'ordinata del punto M (di ascissa = l) . a e b possono variare a piacimento tra 0 e l anche con a diverso da b. Devo calcolare le aree A1 del quadrilatero ARQP, l'area A2 del quadrilatero NQMD, l'area A3 del triangolo CPN e l'area A4 del triangolo BMR. Posso calcolare le aree dei singoli triangoli partendo dalle coordinate dei rispettivi tre vertici e le aree dei quadrilateri come somme di triangoli, ricadendo sempre nel caso di area di un triangolo.
Le coordinate dei punti coinvolti R, Q e P, non ancora note, posso determinarle considerando tali punti come intersezione tra due rette, di cui è facile determinare le rispettive equazioni cartesiane (rette passanti per due punti). Una volta calcolate le aree in funzione di a e b (l è un parametro che posso considerare come costante) , dimostro che per qualunque valore di a e di b risulta:
A1 = A2+A3+A4
Purtroppo il ragionamento è semplice , ma le formule che ne vengono fuori no... Non escludo che ci sia una via alternativa e magari meno difficile da percorrere.
basta ricordare le aree dei triangoli e del quadrato e ben poco di più...
Ci sono, credo.
Area di AMC =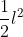 (1)
(1)
Area di ABN =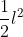 (2)
(2)
Cioè: AMC = ABN.
Inoltre, se AMC = metà area del quadrato ABCD, allora deve essere (vedere aree nella figura del mio commento precedente):
AMC = ARQP + ABR + PQN = BMR + QRM + NQMD + APC + CPN
da cui:
ARQP = CPN + NQMD + BMR + [APC + QRM - (ABR + PQN)] (5)
ora
APC + QRM = AMC - ARQP
e
ABR + PQN = AMN - ARQP
poichè si è visto che AMC = AMN, risulta allora:
APC+QRM = ABR + PQN , quindi la (5) diventa:
ARQP = CPN + NQMD + BMR
Come volevasi dimostrare
;-)
ops... verso la fine ho scritto
"ABR + PQN = AMN - ARQP
poichè si è visto che AMC = AMN, risulta allora:"
ovviamente voleva essere:
ABR + PQN = ABN - ARQP
poichè si è visto che AMC = ABN, risulta allora:
Tutto chiaro, Arturo, tranne una cosa: tu parti dall'ipotesi AMC = ABN = 1/2 ABCD
Non mi sembra che tu lo abbia ricavato in qualche modo, quindi esiste un teorema?
Ciao Daniela, no no, nessun teorema. AMC = ABN perché valgono entrambi metà dell'area del quadrato. E che valgano metà dell'area del quadrato discende dal fatto che ciascuno dei due triangoli ha come base e come altezza proprio il lato del quadrato. A volte , magari per (de)forma mentis, penso a soluzioni complicate, quando invece quella più semplice mi sta davanti e aspetta solo che io me ne accorga
Hai proprio ragione, spesso le soluzioni più ovvie sono evidenti ma non le vediamo... Proprio come l'area di quei triangoli!
Grazie e buona domenica