QUIZ matematico: semplifichiamo le cose complicate **

21/08/16

QUIZ matematico: semplifichiamo le cose complicate **

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:1

Un’espressione che sembra particolarmente lunga e complessa si può ridurre a qualcosa di veramente compatto e semplice. Mettiamoci alla prova…

C’è sempre chi vuole complicare le cose semplici… Ne vediamo un esempio nell’espressione che segue:

1/2! + 2/3! +3/4! + …. + (n-1)/n! = ?

Ricordiamo, se ce ne fosse bisogno, cosa s’intende con quel punto esclamativo inserito dopo un numero intero n. Il suo nome è fattoriale del numero e non è altro che il prodotto di tutti i numeri interi da 1 al numero n, ossia:

n! = 1∙ 2 ∙ 3 ∙ 4∙ ….∙ n

come spiegato QUI.

Calcolare quanto vale l’espressione precedente è un bella "scocciatura". Immaginate, poi, se il numero n fosse molto grande…

Proviamo a semplificarla al massimo (ossia eseguendo meno calcoli e riducendone l’espressione generale). Vediamo chi ama la massima semplicità…

La soluzione QUI

Articoli correlati

1 commento

  1. Arturo Lorenzo
    21/08/2016 at 14:54

    \frac{n-1}{n!}=\frac{n}{n!}-\frac{1}{n!}=\frac{n}{n(n-1)!}-\frac{1}{n!}=\frac{1}{(n-1)!}-\frac{1}{n!}

    Ora

    \sum_{k=2}^{n}(\frac{1}{(k-1)!}-\frac{1}{k!})=(\frac{1}{1}-\frac{1}{2!})+(\frac{1}{2!}-\frac{1}{3!})+(\frac{1}{3!}-\frac{1}{4!})+...+(\frac{1}{(n-1)!}-\frac{1}{n!})

    eliminando le parentesi e i termini opposti, otteniamo:

    \sum_{k=2}^{n}(\frac{1}{(k-1)!}-\frac{1}{k!})=1-\frac{1}{n!}

    al tendere di n all'infinito, il termine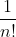 \frac{1}{n!} tende a zero, per cui in definitiva la nostra somma originaria vale 1.

     

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.