Quiz: L’elastico nascosto **
Questo è un quiz di pura logica, senza formule o concetti matematici o fisici. Come sempre in questi casi, può essere risolto immediatamente o può aver bisogno di ore di ragionamenti. Insomma, è anche questione di fortuna oltre che di prontezza.
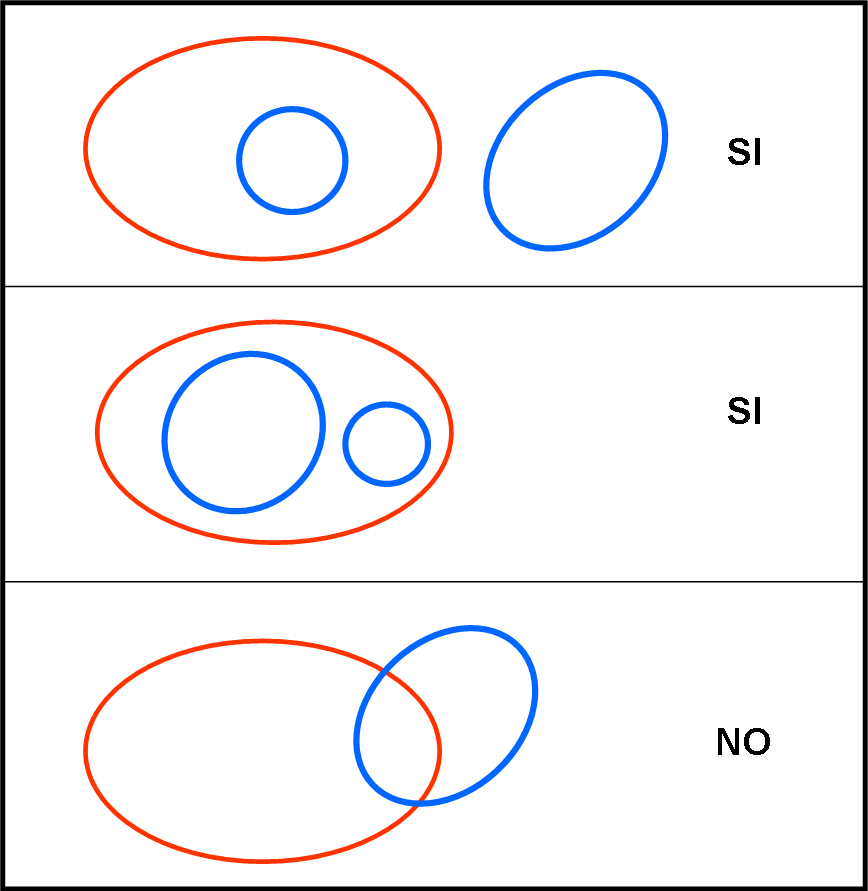
Abbiamo a disposizione sei elastici (chiusi), tre di colore rosso e tre di colore blu. Gli elastici possono avere lunghezza diversa e si possono, ovviamente, disporre secondo forme non banali. La cosa fondamentale è che nessuno di essi si intrecci con un altro, qualsiasi colore abbia. In altre parole, un elastico può stare dentro un altro elastico, ma non può attraversarlo. Le regole sono sintetizzate in Fig. 1.
Sistemati i sei elastici copriamone una parte con uno schermo scuro, ottenendo la Fig. 2.
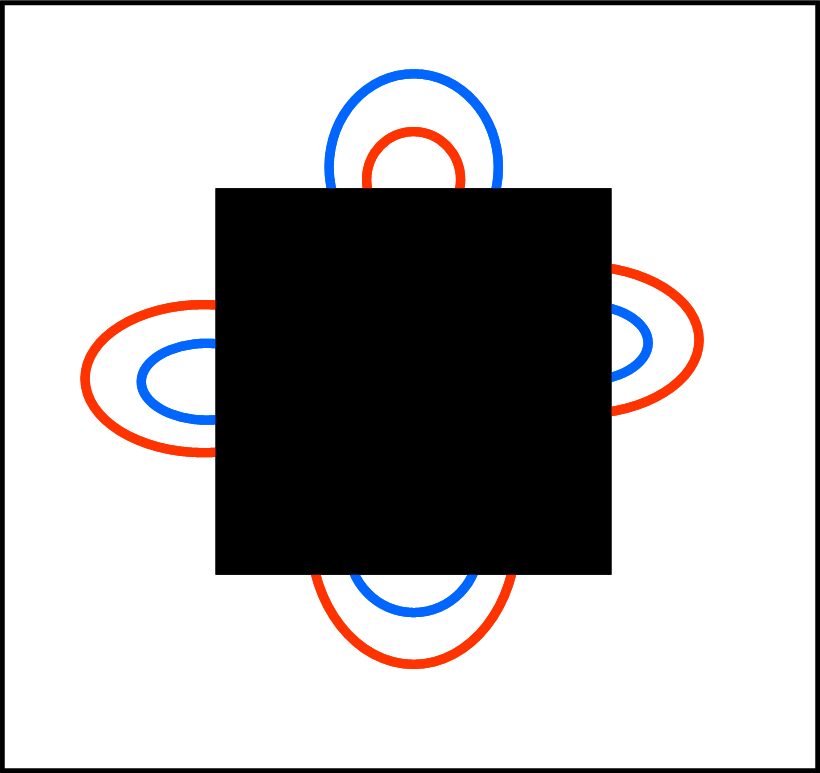
Possiamo dare un aiuto importantissimo, più che sufficiente per risolvere il quiz, dicendo che nella figura si vedono parti di cinque elastici. Uno solo è completamente oscurato.
La domanda è: “Di che colore è l’elastico completamente nascosto ?”
Ovviamente, dovete anche spiegare il ragionamento fatto…






6 commenti
E' rosso!
C'è un elastico rosso grande messo a T che contiene due elastici blu e uno rosso (oscurato)
non dico ancora niente, ovviamente...
per me e' Rosso.
Ragionamento. I due elastici in alto non possono essere parte degli altri, altrimenti, avendo i colori invertiti (blu esterno, rosso interno) si intersecherebbero. Quindi quei due sono isolati, contiamo due.
Gli elastici visibili nelle porzioni laterali e inferiori non possono appartenere ad un unico elastico (uno blu uno rosso), perche' altrimentii in totale ne vedremmo quattro, mentre il quiz ne pone visibili 5.
L'unica condizione che soddisfa la visibilita' di 5 elastici e che delle tre porzioni in basso si vedano tre elastici, e questi possono essere solo uno rosso e due blu. Non puo' essere viceversa perché il rosso e' sempre esterno... cioe' contiene sempre i blu, e due rossi implicherebbero un'intersezione. Quindi vediamo due rossi e tre blu, manca un rosso.
Indichiamo con CP l'elastico considerato
ove C = {R,B} cioè rosso o blu
e P = {N,E,S,W} cioè posizione nord, est,sud,ovest
a) Essendovi 4 elastici blu in vista è ovvio che almeno due di essi siano lo stesso elastico (vincolo numerico =3);
b) L'elastico BN non può congiungersi con nessuno dei BE,BS,BW in quanto l'intreccio coi rossi RE,RS,RW è proibito;
c) in virtù di a) e b) RN è contenuto in BN;
rimangono le possibilità:
d1) RE = RW e BE=BW quindi RS,BS isolati
d2) RE = RS e BE=BS quindi RW,BW isolati
d3) simmetrica a d2)
d4) RW=RE=RS e BW=BE=BS
d5) RW=RE=RS , BW=BS e BE, RE isolati
d6) simmetrica a d6)
Analisi dei casi:
d1) RN , RE=RW e RS sono 3 rossi in vista e BN , BE=BW e BS 3 blu in vista . Non possibile
d2) RN , RE=RS e RE sono 3 rossi in vista e BN , BE=BS e BE 3 blu in vista. Non possibile
d3) simmetrica a d2) . Non possibile
d4) RN , RW=RE=RS sono 2 rossi in vista e 2 blu in vista. Non possibile.
d5) RN,RW=RE=RS sono 2 rossi in vista mentre BN , BW=BS e BE sono 3 blu in vista
d6) simmetrico a d5)
quindi l'unico caso valido è d5 o d6 che comportano 1 rosso nascosto.
Ciao Zappi,
per prima cosa ho capito che gli elastici visibili nella parte superiore devono per forza essere isolati dagli altri perché se no si intreccerebbero. Poi ho dedotto che l'elastico rosso visibile è uno solo e contiene due elastici blu, perché se fossero due rossi si intreccerebbero con il blu. Quindi rimane un rosso nascosto.
A questo punto non posso che dirvi BRAVI! Era abbastanza facile, ma voi siete stati rapidissimi. D'altra parte chi frequenta questo circolo non è certo una persona banale...