Le soluzioni sono state molteplici, ma devo ammettere che il metodo utilizzato da Arturo è decisamente il migliore. Può darsi che si possa risolvere più velocemente, ma non riesco a trovare niente di meglio. Se qualcuno ci riesce, tanti complimenti! Come soluzione riporto, quindi, pari pari quella scritta nel commento di Arturo… Bravi tutti, comunque!

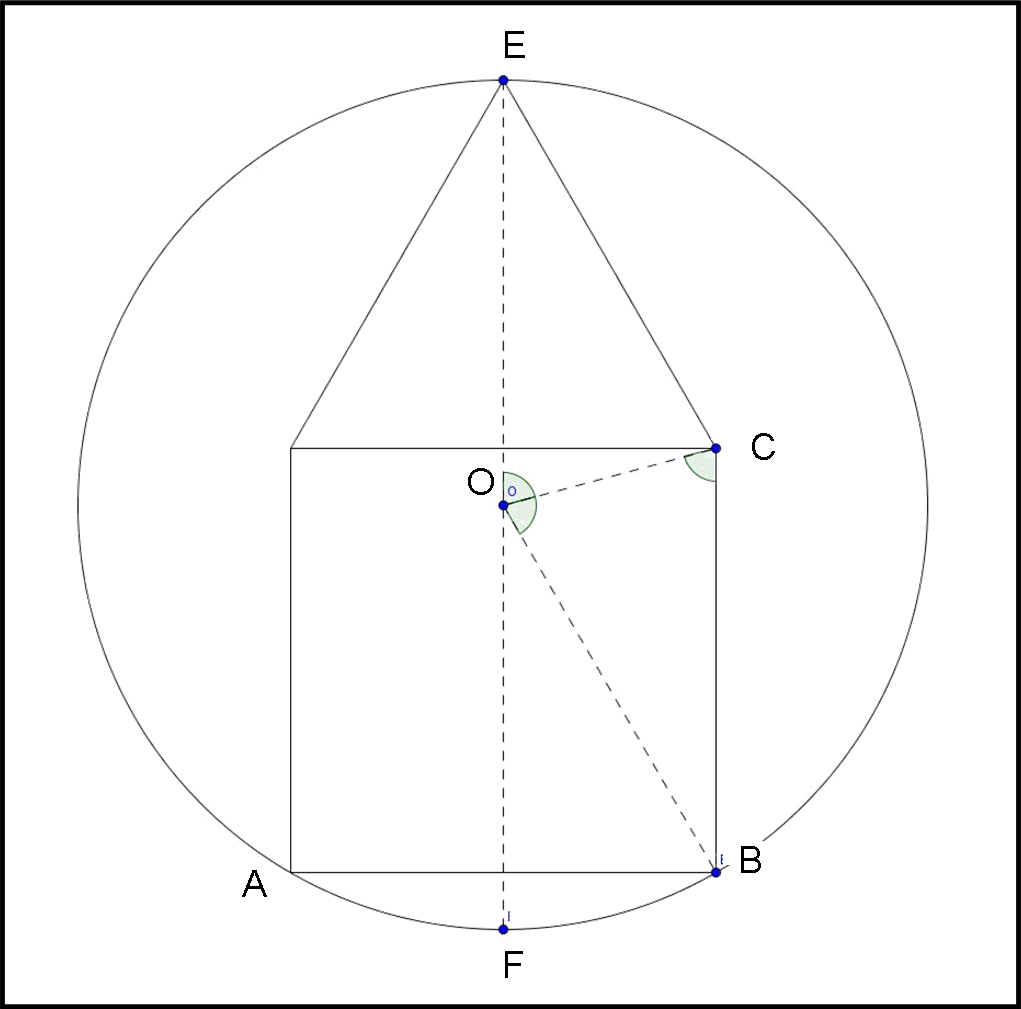
La circonferenza deve passare per B, E ed A. Per la simmetria della casetta, il centro O della circonferenza circoscritta non può che giacere sulla retta passante per E e perpendicolare alla base del quadrato. Consideriamo il punto O come centro della circonferenza di cui però non conosciamo ancora il raggio in funzione del lato del quadrato.

Consideriamo ora i due triangoli EOC e BOC. Essi sono congruenti (in poche parole uguali), perché hanno i tre lati rispettivamente uguali. Infatti risulta:

EO = OB perché entrambi raggi di una stessa circonferenza (O è stato scelto come centro)

EC = BC per costruzione (il lato del tetto è uguale al lato della casetta)

OC in comune ai due triangoli

Essendo i due triangoli congruenti, allora risulta anche l’uguaglianza tra gli angoli:

EOC = BOC      …. (1)

Considerando, ora, le rette parallele EF e BC (parallele per costruzione), tagliate dalla trasversale OC, risulta l’uguaglianza degli angoli alterni interni

EOC = BCO      …. (2)

Dalle (1) e (2) deriva, quindi, l'uguaglianza tra gli angoli:

BOC = BCO

Cioè il triangolo BOC è isoscele e, quindi, BO = BC.

Ma BC è il lato del quadrato di partenza (la cui lunghezza è  di 10 cm). Per cui anche il raggio BO deve essere uguale al lato, ossia a 10 cm.

La dimostrazione è ineccepibile e non accetta niente come dato di fatto se non i dati di partenza. Ripeto ancora: Questo articolo-soluzione porta il mio nome, ma è un falso! L’autore è solo e soltanto Arturo, che speriamo ci delizi presto con qualche nuovo articolo sulla geometria a tre dimensioni…

Questo è il modo migliore per vedere crescere un vero “circolo” scientifico-divulgativo. Sono realmente contento e un po’ commosso. Grazie a tutti quelli che dedicano il loro tempo per migliorarci...

Il QUIZ lo trovate QUI