Categorie: Matematica
Tags: cilindro formica geometria percorso minimo quiz
Scritto da: Vincenzo Zappalà
Commenti:20
QUIZ: Un barattolo e una formica (prima parte) **
Questa prima parte del quiz è di una difficoltà molto moderata. Invito a risolverlo in modo molto rapido. Se tutto va come prevedo, avremo da discutere parecchio quando apriremo la seconda parte.
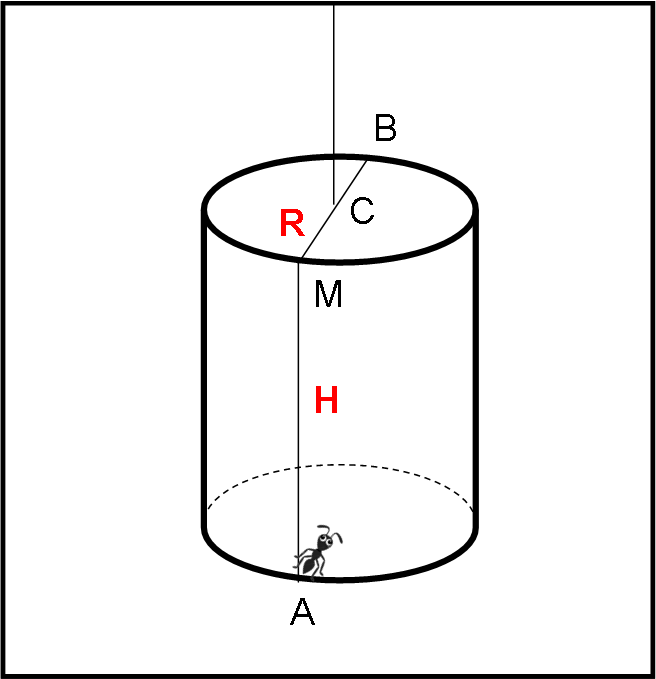
Per il nostro quiz sono necessari un barattolo chiuso di forma cilindrica che immaginiamo sospeso attraverso una corda sottilissima. La configurazione vuole solo dire che qualsiasi percorso lungo l’esterno del barattolo è possibile. Il secondo personaggio è una formica che si trova nel punto A. La domanda è molto semplice: “Qual è il percorso più breve che deve fare la formica per raggiungere il punto B che si trova nella parte superiore ed è simmetrico ad A rispetto al centro del barattolo”.
Sia R = CM = CB il raggio delle basi del cilindro e H = MA la sua altezza, come indicato in figura.
Seconda parte QUI
20 commenti
A prima vista avrei detto sale dritto sulla verticale, poi prosegue lungo il diametro. Quindi AM+MB.
Ma se sale elicoidalmente, sulla superficie del cilindro, percorre l'ipotenusa di un triangolo rettangolo che ha come cateti la semi-circonferenza del cilindro e la sua altezza. Applicando pitagora la lunghezza del percorso e' la radice quadrata di (MB x 1,57 al quadrato + AM al quadrato), e credo sia la piu' breve possibile.
qualche calcoletto, Paolo e qualche confronto?
Credo proprio che Paolo abbia ragione, infatti se si taglia il cilindro lungo AM e lo si distende sul piano, la sua superficie laterale si trasforma in questo rettangolo
e il percorso elicoidale corrisponde al segmento AB, sicuramente più corto di AM+MB
siete proprio sicuri? Per qualsiasi altezza H? Pensateci bene...
Se ho "affettato" bene il cilindro, non vedo come AB possa non essere il percorso più breve, qualunque sia la lunghezza di AM... ma di sicuro c'è qualcosa che mi sfugge, figuriamoci se poteva essere così semplice
Hai ragione... risposta affrettata. E il bello che avevo fatto la prova con due altezze... una la meta' dell'altra e funzionava. Purtroppo avevo preso cilindri un po' altini. Con altezze minori e' piu' corta AM + MB...
Minori pero' non vuol dire molto, vorrai sapere l'altezza per la quale esiste indifferenza tra percorrere l'ipotenusa i segmenti AM+MB... giusto ?
cara Daniela,
pensa a un cilindro che è alto pochissimo, un dH circa 0. Il suo diametro, ossia l'attraversamento della base superiore, è uguale a 2R. La spirale lungo il cilindro è uguale a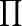
R... 3.14 è maggiore di 2...
Vi è una relazione che lega i due percorsi e quindi ...
la risposta vale anche per Paolo, ovviamente...
In effetti il cilindro srotolato mi aveva fatto perdere di vista la visione tridimensionale... è questa la soluzione?
Ops... ovviamente il pigreco è al quadrato!
Ho seguito tutti i passaggi di Daniela, secondo me va benone... in realta' l'egualianza iniziale l'avevo scritta nel medesimo modo, ma non ricordavo che (x+y)2 si semplifica in x2 + y2 +2xy... anche oggi ho ri-imparato qualcosa.... (non ridete).
E chi ride... è il bello del nostro Circolo! Imparare cose nuove e riaprire cassettini della memoria dopo tanti anni è meraviglioso
Ora aspettiamo la "sentenza" del Prof. sui vari passaggi...
speriamo che sia di buon umore 
Il "prof" è di buon umore... ma ricordatevi cosa c'è scritto nel titolo... : prima parte. Come mai? Non vorrei inserire subito la seconda parte ("leggermente" più difficile, ma non poi tanto), quindi vi prego di aspettare ancora un pochino. Nel frattempo cominciate a pensare: "Ho agito nel modo più corretto e logico, ossia più matematico? ". Scusate se faccio un po' il misterioso, ma questi quiz vengono proprio DIVORATI... e vorrei dare il tempo ad altri lettori. Poi cominceremo veramente a divertirci con la formichina.
Dubito fortemente di avere agito nel modo più corretto e logico, ma di avere preso una scorciatoia dettata da ciò che "si vede". Comunque, non so Paolo, ma io mi fermo qui e aspetto la soluzione... non vorrei che riaprire troppi cassettini in una volta sola fosse "traumatico" per le mie povere sinapsi di mezz'età!
No, non ho detto che avete dato una risposta sbagliata. Dico soltanto che per potere dire di aver dato la soluzione giusta non avete considerato la situazione in modo matematicamente generale... Lo studio di funzioni serve anche a questo... Basta, se no finisco per inserire la seconda parte troppo presto...
come sempre sei sulla strada buona... però non mi torna tanto la funzione monotona... Può darsi che sbagli io... devo provarci... Complimenti comunque!!!!! Hai compreso il vero succo del discorso. Prima di trarre conclusioni bisogna analizzare il problema in modo veramente generale e non limitarsi agli estremi. Non sempre vale la regola di questo o quello...
caro Leandro....
occhio alla derivata del coseno!
Vero, giudizio troppo affrettato. Non è monotona. Funzione troppo complessa per una analisi non numerica. In questo caso è meglio affidarsi ai vecchi odiati computer.
non cedere Leandro... si può fare senza computer. Oggi, se riesco, imposto la seconda puntata e ci puoi lavorare sopra (anche se avevi già capito il senso del quiz
). Ancora complimenti... 